Оценивание показателей области

3. Оценивание показателей «области»

Обозначения:

 - «область», т.е. некоторое подмножество совокупности U;

 - объем  (неизвестно);

 - относительный объем (доля) ;

;

- единицы выборки, относящиеся к ;

 - объем ;

  - относительный объем ;

Рекомендуемые материалы

.

3.1. Оценивание объема области

Определим индикаторную переменную (z) следующим образом:

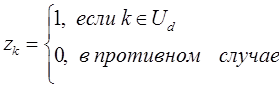
Тогда

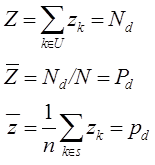
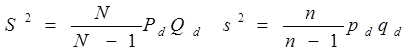
Теорема 3.

Для доли и объема области   имеем

 - несмещенная оценка

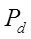
 - несмещенная оценка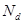

Замечание:

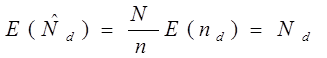
откуда

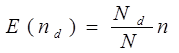
Вообще,  подчиняется закону распределения H(n,N,) :

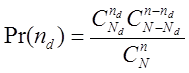
Теорема 4.

Для оценок доли и объема области   имеем

- дисперсия оценок (по генеральной совокупности):

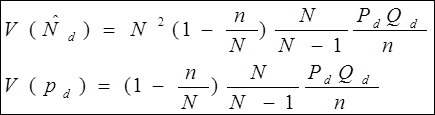
- оценка дисперсии оценок (по выборке):

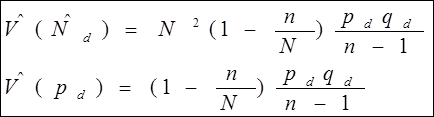
Это следует из результатов п.2.3

3.2. Оценивание суммы по области

Требуется оценить сумму переменной (y) по области.

Определим для U переменную следующим образом:

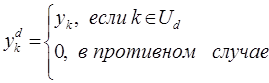
Тогда

- сумма, которую требуется оценить.

Как следует из п. 2.2.,

1) несмещенная оценка  задается  формулой:

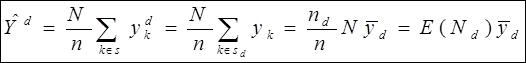
где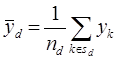 

2) дисперсия и оценка дисперсии задаются соотношениями:

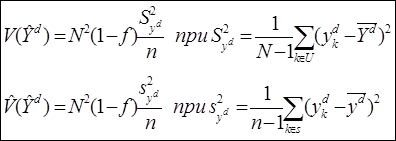
Замечание.

1. Положим, что

,

т.е. так связаны естественное () и формальное () средние  переменной (y) по области .

Положим

- дисперсия (y) в ,

Тогда

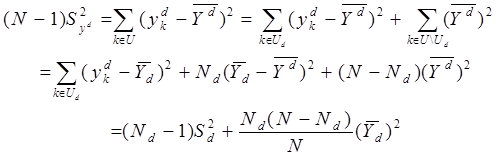
Следовательно,

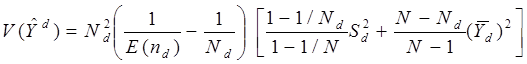
Т.е. это выражение дисперсии оценки через естественные характеристики области.

2. Если объем  области известен. то может быть предложена другая "естественная" оценка для :

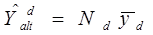
т.е. несмещенная оценка   заменяется на известное истинное значение .

Обычно,  предпочтительнее, чем.

3.3. Оценивание среднего по области

Вам также может быть полезна лекция "3.7 Цветовая индукция".

Требуется оценить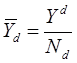

· Если  известно, то можно воспользоваться следующей формулой:

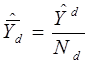
· Но можно также воспользоваться выражением:

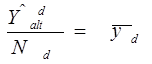
независимо от того, известно или неизвестно ;  которое, как правило, лучше предыдущего;  и которое является интуитивным!