Примеры линейных пространств

Примеры линейных пространств.

1). Пространства и ,состоящие из всевозможных (упорядоченных) наборов из n чисел (соответственно -- действительных или комплексных). Сложение и умножение определяются формулами

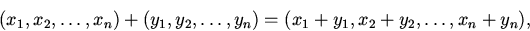
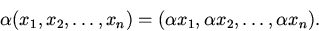
С этими пространствами вы достаточно хорошо знакомы по курсам алгебры и анализа.

2). Непрерывные (действительные или комплексные) функции на некотором отрезке [a, b] с обычными операциями сложения функций и умножения их на числа образуют линейное пространство C[a, b], являющееся одним из важнейших в анализе и уже встречавшееся вам, например, при изучении функциональных рядов.

3). Пространство быстроубывающих функций ,с которым вы работали, изучая преобразование Фурье.

4). Пространство l₂, в котором элементами служат последовательности чисел (действительных или комплексных)

Рекомендуемые материалы

удовлетворяющие условию

с операциями

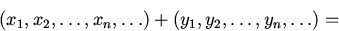
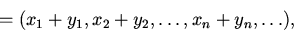
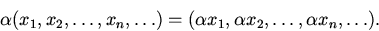
является линейным пространством. Тот факт, что сумма двух последовательностей, удовлетворяющих условию (1), также удовлетворяет этому условию, вытекает из элементарного неравенства

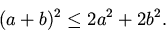
Конечный набор элементов линейного пространства L называется линейно зависимым, а сами элементы -- линейно зависимыми, если существуют такие числа ,не все равные нулю, что

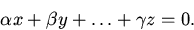
В противном случае эти элементы называются линейно независимыми. Иными словами, элементы называются линейно независимыми, если из равенства

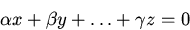
Обратите внимание на лекцию "11 Групповой конфликт".

вытекает, что .

Бесконечная система элементов пространства L называется линейно независимой, если любая ее конечная подсистема линейно независима.

Если в пространстве L можно найти n линейно независимых элементов, а любые n+1 элементов этого пространства линейно зависимы, то говорят, что L имеет размерность n. Если же в L можно указать систему из произвольного конечного числи линейно независимых элементов, то говорят, что пространство L бесконечномерно.

Легко понять, что в приведенных выше примерах 2)-4) пространства бесконечномерны, а в примере 1) -- имеют размерность n.

Непустое подмножество L' линейного пространства L называется подпространством, если оно само образует линейное пространство по отношению к опрелеленным в L операциям сложения и умножения на число.

Иначе говоря, есть подпространство, если из ,следует, что при любых числах .