Вычеты
Вычеты
Опр.  -изолированная особая точка.
-изолированная особая точка.  называется вычетом, где
называется вычетом, где  - коэффициент при -1 степени в разложении ряда Лорана:
- коэффициент при -1 степени в разложении ряда Лорана: 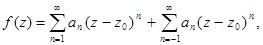
Основная теорема о вычетах.
Если G – односвязная область, Г – замкнутый контур, Г ограничевает G, G содержит конечное число изолированных особых точек  функции
функции  , то
, то
 .
.
Док-во:
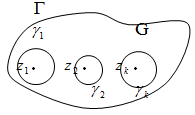
Окружит каждую особую точку  окружностью
окружностью  так, чтобы внутри
так, чтобы внутри  не было других особых точек, и чтобы
не было других особых точек, и чтобы  и
и  не пересекались(i
не пересекались(i j).
j).
 .
.
Рекомендуемые материалы
Вычисление вычетов
1.
Утв. Если  - устранимая особая точка
- устранимая особая точка  , то
, то  (Т.к. главная часть ряда Лорана не содержит ни одного члена
(Т.к. главная часть ряда Лорана не содержит ни одного члена  )
)
2.
а) Утв. Если  -простой полюс
-простой полюс  (полюс кратности 1), то
(полюс кратности 1), то  .
.
Док-во:
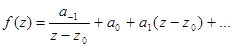
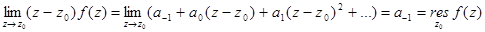
Пример.
 ,
, 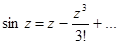
 имеет простой полюс.
имеет простой полюс.
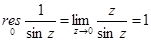
б) Утв. Если  ,
, ,
, ,
, , то
, то  .
.
Док-во:
 -полюс I порядка
-полюс I порядка 
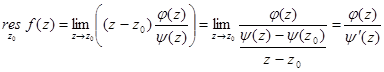
3.
Утв. Если  -полюс порядка n
-полюс порядка n  , то
, то  .
.
Док-во:
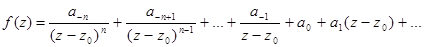



Переходим к  и делим на
и делим на  :
:
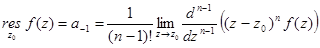
Пример1.
 ;
;
Пример2.
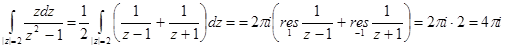
Опр. 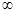 - изолированная особая точка
- изолированная особая точка  ,
,
 , где Г- замкнутый контур.
, где Г- замкнутый контур.
Утв. Если  , то
, то  .
.
Док-во:
1)  .
.
2) С: { }
}
 ,
, 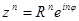
при 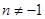
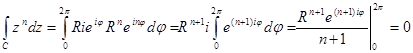
3)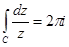

4) 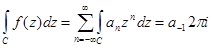
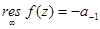
Теорема. Если 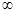 -изолированная особая точка, кроме
-изолированная особая точка, кроме 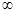 имеется конечное число особых точек, то
имеется конечное число особых точек, то 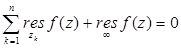
Лекция "Структурно-логические модели надежности ПО" также может быть Вам полезна.
Док-во:
Возьмем замкнутый контур С, охватывающий все особые точки, кроме 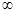
 ;
;
 ;
;
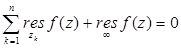 ;
;

















