Особые точки функций комплексного переменного
Особые точки функций комплексного переменного
Опр. Особой точкой функции  называется точка в которой
называется точка в которой  не определена или не дифференцируема.
не определена или не дифференцируема.
Опр. Особая точка называется изолированной, если  такая ее окрестность, в которой нет других особых точек.
такая ее окрестность, в которой нет других особых точек.
Утв. Если 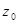 - изолированная особая точка
- изолированная особая точка  , то в окрестности
, то в окрестности 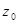 ,
,  раскладывается в ряд Лорана.
раскладывается в ряд Лорана.
Классификация особых точек
Опр1. Особая точка называется устранимой, если в ряде Лорана в окрестности этой точки отсутствует главная часть.
Опр2. Изолированная особая точка называется полюсом, если главная часть ряда Лорана в окрестности этой точки имеет конечное число членов:
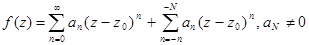
Рекомендуемые материалы
Число N называется кратностью (порядком полюса).
Утв. Если 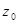 - полюс
- полюс  , то
, то  .
.
Док-во: 

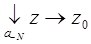
Опр3. Изолированная особая точка называется существенно особой, если главная часть разложения в ряд Лорана в окрестности этой точки содержит бесконечное число членов.
Связь между нулем и полюсом
Утв1.  имеет в точке
имеет в точке 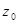 нуль порядка n
нуль порядка n 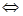
 имеет в точке
имеет в точке 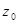 полюс порядка n.
полюс порядка n.
Док-во: {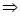 }
}
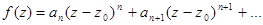
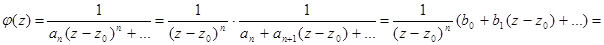

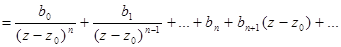
Утв2.  имеет существенно особую точку в точке
имеет существенно особую точку в точке 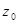
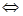
 имеет в
имеет в 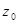 неизолированную особую точку ИЛИ существенно особую точку.
неизолированную особую точку ИЛИ существенно особую точку.
Пример.
 ;
;
 ;
;

 ;
;  ;
;
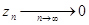
Таким образом, получаем не изолированную особую точку.
Утв3. Если  ,
,
 ,
,
 ,
,
то  имеет при:
имеет при:
1)m n устранимую особую точку,
n устранимую особую точку,
2)m>n полюс порядка n-m.
Док-во: {для 2}

 ;
;
Теорема Сохоцкого.
Если 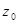 -существенно особая точка функции
-существенно особая точка функции  , то
, то 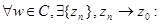
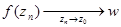 .
.
Док-во:
1)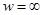
а) 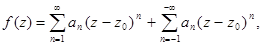
 -сходится при
-сходится при 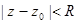
 сходится при
сходится при 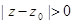
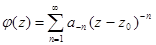
б) Предположим противное:
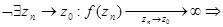
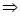
 ограничена в окрестности точки
ограничена в окрестности точки 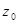 .
.
в) 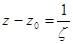
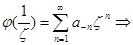
 при
при  (т.е.
(т.е.  ограничена в окрестности
ограничена в окрестности  ).
).
г)В круге 
 ограничена, как непрерывная функция в замкнутой области.
ограничена, как непрерывная функция в замкнутой области.
д) Из б), в), г) следует  ограничена на всей комплексной плоскости.
ограничена на всей комплексной плоскости.
е)  ограничена на С,
ограничена на С,  аналитическая, по теореме Ляувилля
аналитическая, по теореме Ляувилля 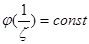
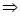 противоречие.
противоречие.
2) 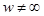
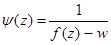
а) 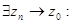
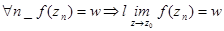
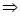
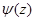 имеет не изолированную особую точку.
имеет не изолированную особую точку.
б)
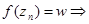
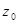 -изолированная особая точка
-изолированная особая точка 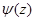
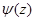 имеет изолированную особую точку в
имеет изолированную особую точку в 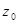
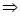
 имеет существенно особую точку
имеет существенно особую точку 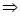 по Утв2
по Утв2 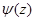 имеет существенно особую точку в
имеет существенно особую точку в 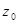
 по 1)
по 1) 
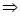
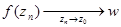
Вам также может быть полезна лекция "Лекции 2 - Классификация ПР и системы координат".
Теорема доказана.
Особые точки в бесконечности
Утв. Если  -изолированная особая точка
-изолированная особая точка  , то
, то 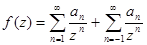
Док-во:
Пусть  . Раскладываем
. Раскладываем  в окрестности нуля:
в окрестности нуля:
 .
.






















