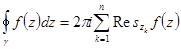Вычет в изолированной особой точке. Доказать теорему Коши о вычетах
Вычет в изолированной особой точке. Доказать теорему Коши о вычетах
Пусть функция  - аналитическая в некоторой проколотой окрестности точки
- аналитическая в некоторой проколотой окрестности точки  . Если существует комплексное число A, доопределяя которым функцию в самой точке, удается сделать функцию аналитической в окрестности точки
. Если существует комплексное число A, доопределяя которым функцию в самой точке, удается сделать функцию аналитической в окрестности точки  (включая точку
(включая точку  ), то точка
), то точка  называется правильной точкой функции
называется правильной точкой функции  . Если такого числа не существует, то точка
. Если такого числа не существует, то точка  называется изолированной особой точкой
называется изолированной особой точкой  (однозначного характера).
(однозначного характера).
Если  - правильная точка функции
- правильная точка функции  , то
, то  .
.
Общая теорема о вычетах.
|
Лекция "23. Письма русского путешественника" также может быть Вам полезна. Тогда |
|
Доказательство. По интегральной теореме Коши для многосвязной области  . Вычислим интеграл
. Вычислим интеграл  . Разложим функцию
. Разложим функцию  в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки  и подставим в интеграл. По равномерной сходимости степенного ряда внутри круга сходимости, проведем почленное интегрирование и используем полученный ранее результат
и подставим в интеграл. По равномерной сходимости степенного ряда внутри круга сходимости, проведем почленное интегрирование и используем полученный ранее результат  =
= .
.
 =
= .
.
Тогда  =
= .
.


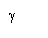
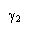
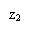

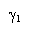


 Пусть функция
Пусть функция  - аналитическая в области
- аналитическая в области  и на ее границе – кусочно-гладком контуре g за исключением конечного числа изолированных особых точек
и на ее границе – кусочно-гладком контуре g за исключением конечного числа изолированных особых точек  , лежащих внутри области
, лежащих внутри области