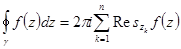Вычет аналитической функции в изолированной особой точке. Вычет в бесконечно удаленной точке. Доказать теорему о сумме вычетов
Вычет аналитической функции в изолированной особой точке. Вычет в бесконечно удаленной точке. Доказать теорему о сумме вычетов. В том случае, когда точка  - существенно особая точка, вычет в ней вычисляется единственным способом – непосредственным разложением функции в ряд Лорана и вычислением коэффициента при –1 степени.
- существенно особая точка, вычет в ней вычисляется единственным способом – непосредственным разложением функции в ряд Лорана и вычислением коэффициента при –1 степени.
Пример. 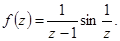
Здесь  - существенно особая точка. Разложение в ряд Лорана в окрестности
- существенно особая точка. Разложение в ряд Лорана в окрестности  :
:
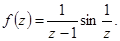
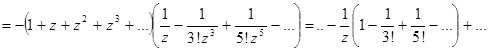
 .
.
Вычетом функции в бесконечно удаленной точке  называется коэффициент
называется коэффициент  , (взятый со знаком минус коэффициент при –1 ой степени в разложении в ряд Лорана в окрестности бесконечно удаленной точки).
, (взятый со знаком минус коэффициент при –1 ой степени в разложении в ряд Лорана в окрестности бесконечно удаленной точки).
Общая теорема о вычетах.
|
Рекомендуемые материалы-50% Статически определимые балки -43% Теория поля -62% Числовые ряды -60% РК №1, №2 и №3 Полностью решенные [ПОЛНОСТЬЮ ВЕРНО by БЕЛОУСОВ] Д/З 9 ВАРИАНТ [ВСЯ КОМБИНАТОРИКА] [for IU7] -62% Числовые ряды Тогда |
|
Доказательство. По интегральной теореме Коши для многосвязной области  . Вычислим интеграл
. Вычислим интеграл  . Разложим функцию
. Разложим функцию  в ряд Лорана в окрестности точки
в ряд Лорана в окрестности точки  и подставим в интеграл. По равномерной сходимости степенного ряда внутри круга сходимости, проведем почленное интегрирование и используем полученный ранее результат
и подставим в интеграл. По равномерной сходимости степенного ряда внутри круга сходимости, проведем почленное интегрирование и используем полученный ранее результат  =
= .
.
 =
= .
.
Тогда  =
= .
.
Если Вам понравилась эта лекция, то понравится и эта - Специфика геоэкономического и геополитического положения России.
Теорема. Сумма вычетов функции по всей расширенной плоскости равна нулю.
Доказательство. Выберем контур  так, чтобы все особые точки функции лежали внутри контура. Тогда при обходе контура в положительном направлении надо учитывать
так, чтобы все особые точки функции лежали внутри контура. Тогда при обходе контура в положительном направлении надо учитывать
особые точки, попавшие внутрь контура, т.е. все особые точки конечной плоскости. По общей теореме о вычетах 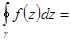
 . С другой стороны, при обходе контура в отрицательном направлении мы должны учитывать только бесконечно удаленную точку и интеграл получится тем же, но со знаком «минус» (свойство интеграла). Поэтому -
. С другой стороны, при обходе контура в отрицательном направлении мы должны учитывать только бесконечно удаленную точку и интеграл получится тем же, но со знаком «минус» (свойство интеграла). Поэтому -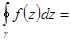
 . Складывая эти интегралы, получим
. Складывая эти интегралы, получим
 .
.
Следствие. Сумма вычетов функции по всей конечной плоскости равна вычету функции в бесконечно удаленной точке, взятому со знаком «минус».
Доказательство. По предыдущей теореме  . Отсюда
. Отсюда  .
.



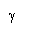
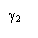
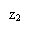

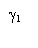


 Пусть функция
Пусть функция  - аналитическая в области
- аналитическая в области  и на ее границе – кусочно-гладком контуре g за исключением конечного числа изолированных особых точек
и на ее границе – кусочно-гладком контуре g за исключением конечного числа изолированных особых точек  , лежащих внутри области
, лежащих внутри области