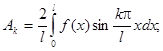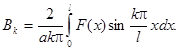Решение задачи Коши методом разделения переменных (Метод Фурье)
2020-06-032021-03-09zzyxelСтудИзба
Решение задачи Коши методом разделения переменных.
(Метод Фурье.)
Решение уравнения
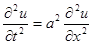
будем искать в виде 
при граничных условиях:
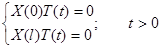
Тогда X(0) = X(l) = 0.
Подставим решение в исходное уравнение:
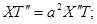
Рекомендуемые материалы
FREE
Бараненков Г. С., Демидович Б. П., Ефименко В. А. - Задачи и упражнения по математическому анализу для втузов - 2004
-61%
Решение 4 билетов из РК-1
-66%
Билеты РК №2 с решением
FREE
Методичка Кратные и криволинейные интегралы Добрица, Дубограй, Скуднева
Лабораторная работа №2 (Метод наименьших квадратов)
FREE
Бараненков Г. С., Демидович Б. П., Ефименко В. А. - Задачи и упражнения по математическому анализу для втузов
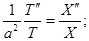
Можно показать, что функции Х и Т имеют вид:
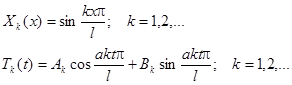
Обратите внимание на лекцию "25 Процедуры и функции".
Все решения исходного дифференциального уравнения, удовлетворяющие граничным условиям, можно записать в виде:
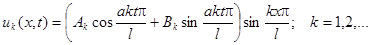
Окончательно решение уравнения колебаний струны можно записать в виде:
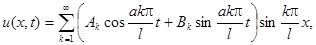
где 
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
