lektsia_10_dlya_studentov_ON (1184631), страница 2
Текст из файла (страница 2)
Найдём направляющий вектор прямой L. Этот вектор перпендикулярен векторам ![]() , следовательно, в качестве вектора
, следовательно, в качестве вектора ![]() можем взять векторное произведение векторов
можем взять векторное произведение векторов ![]() :
:
Далее записываем канонические уравнения прямой L: ![]() .
.
Пример. Прямая L задана общими уравнениями
Выведем канонические уравнения прямой L.
Найдем направляющий вектор:
Окончательный ответ:
3. Взаимное расположение двух прямых в пространстве
Пусть две прямые ![]() заданы каноническими уравнениями:
заданы каноническими уравнениями:
Две прямые в пространстве могут:
Рассмотрим каждый из четырех случаев.
Здесь ![]() ,
, ![]()
![]() точки, принадлежащие прямым
точки, принадлежащие прямым ![]() соответственно;
соответственно; ![]()
![]() направляющие векторы этих прямых.
направляющие векторы этих прямых.



Прямые ![]() параллельны, но не совпадают.
параллельны, но не совпадают.



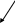
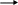
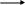
но
но
неверная пропорция.
Две прямые ![]() скрещиваются тогда и только тогда, когда существуют две параллельные плоскости
скрещиваются тогда и только тогда, когда существуют две параллельные плоскости ![]()
![]() такие, что
такие, что ![]() ( см. рисунок ).
( см. рисунок ).
Из рисунка следует, что прямые ![]() скрещиваются тогда и только тогда, когда векторы
скрещиваются тогда и только тогда, когда векторы ![]() некомпланарны. Следовательно, необходимым и достаточным условием того, что прямые
некомпланарны. Следовательно, необходимым и достаточным условием того, что прямые ![]() скрещиваются, является условие
скрещиваются, является условие
Рассмотрим некоторые задачи, связанные со взаимным расположением двух прямых в пространстве.
Задача 1. Найти ![]() расстояние между параллельными прямыми
расстояние между параллельными прямыми ![]() .
.


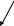





вектор прямых. Ищем ![]() как высоту параллелограмма, построенного на векторах
как высоту параллелограмма, построенного на векторах ![]()
Ищем ![]() как высоту параллелограмма , построенного на векторах
как высоту параллелограмма , построенного на векторах ![]() ( см. рисунок)
( см. рисунок)


Здесь ![]() направляющий вектор прямой,
направляющий вектор прямой, ![]() :
:
Задача 3. Найти угол между прямыми ![]() и
и ![]() , если
, если
Задача 4. Найти расстояние между скрещивающимися прямыми ![]() и
и ![]() , если
, если ![]()








Ищем расстояние ![]() как высоту параллелепипеда, построенного на векторах
как высоту параллелепипеда, построенного на векторах ![]() ( см. рисунок ):
( см. рисунок ):
4.Взаимное расположение прямой и плоскости
Пусть прямая L задана каноническим уравнением:
плоскость P задана общим уравнением:
Прямая L может: 1) пересекать плоскость P в точке A;
2) быть параллельной плоскости P;
3) принадлежать плоскости P.
Рассмотрим эти три случая.
В этом случае векторы ![]() и
и ![]() не являются взаимно ортогональными, следовательно, их скалярное произведение не равно 0:
не являются взаимно ортогональными, следовательно, их скалярное произведение не равно 0:
L
A
P







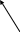




Найдем угол между прямой L и плоскостью P. Обозначим α ![]() искомый угол между прямой и плоскостью, β – угол между нормалью к плоскости и направляющим вектором прямой ( см. рисунок ). Очевидно, что
искомый угол между прямой и плоскостью, β – угол между нормалью к плоскости и направляющим вектором прямой ( см. рисунок ). Очевидно, что
Отсюда
2.Прямая L параллельна P плоскости, но не лежит в плоскости P:
![]() , но
, но ![]() В этом случае векторы
В этом случае векторы ![]() и
и ![]() взаимно перпендикулярны, но точка
взаимно перпендикулярны, но точка ![]() лежащая на прямой L, не принадлежит плоскости P.
лежащая на прямой L, не принадлежит плоскости P.
L




P
3.Прямая L лежит в плоскости P: ![]() В этом случае выполнены условия
В этом случае выполнены условия
![]() ; точка
; точка ![]() , лежащая на прямой L, принадлежит плоскости P. Следовательно, векторы
, лежащая на прямой L, принадлежит плоскости P. Следовательно, векторы ![]() и
и ![]() взаимно перпендикулярны, точка
взаимно перпендикулярны, точка ![]() принадлежит плоскости P.
принадлежит плоскости P.




P
L

























































