Lektsia_8_2007_dlya_studentov_ON (1184622)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

Лекция 8

Решение неоднородных СЛАУ.

Теорема об общем решении.

Метод Гаусса исследования СЛАУ

1. Теорема об общем решении неоднородных СЛАУ

Рассмотрим систему общего вида:

(1)

Система (1) в матричном виде имеет вид

AX = B, _(1')

где

Запишем соответствующую однородную систему:

(2)

В матричном виде система (2) имеет вид

, (2’)

где – нулевой столбец высоты s.

Лемма. Пусть столбцы F и G – решения неоднородной системы (1’) . Тогда столбец F – G является решением однородной системы (2’).

Доказательство.

Имеем:

Отсюда , т.е. столбец F – G является решением однородной системы (2’).

▲

Теорема (об общем решении неоднородной СЛАУ).

Справедлива формула

(3)

Здесь:

общее решение неоднородной СЛАУ (1);

частное решение неоднородной СЛАУ (1);

общее решение однородной СЛАУ (2);

– столбцы ФСР для однородной СЛАУ (2).

Доказательство.

Необходимо доказать два утверждения:

1. Любое выражение вида

при подстановке в систему (1’) вместо X обращает её в верное равенство.

1. Любое решение системы (1’) может быть записано в виде (3).

Докажем 1. Действительно, подставим столбец в систему (1’):

Утверждение 1 доказано.

Докажем 2. Пусть G произвольное решение системы (1’). Докажем, что существуют числа такие, что

,

где – некоторое решение системы (1’).

В силу леммы, столбец , является решением однородной системы (2’);

следовательно, по теореме об общем решении однородной СЛАУ, существуют числа :

▲

1. Алгоритм решения неоднородных СЛАУ

Алгоритм решения неоднородных СЛАУ основан на применении формулы (3). Покажем это на примере.

Задача. Найдем общее решение системы

.

1. ; Rang A=2; базисный минор расположен в верхнем левом углу.

; Rang _=2;

система совместна по теореме Кронекера-Капелли;

небазисное третье уравнение отбрасываем.

1. .

Составляем соответствующую однородную СЛАУ:

.

Ищем ФСР этой системы; (число неизвестных), (ранг матрицы),

Следовательно, ФСР состоит из одного столбца. Базисные столбцы – первый и второй, поэтому считаем базисными переменными, считаем свободной переменной. Ищем столбец ФСР в виде

.

Подставляем в последнюю однородную систему, получим задачу для определения остальных компонент столбца E:

<=> .

Отсюда

.

1. Ищем частное решение неоднородной системы. Вместо свободной переменной подставим произвольное число, например, положим

<=>

Отсюда

.

1. + C .

Ответ.

Замечание. Если бы оказалось, что , а базисный минор расположен в верхнем левом углу, то считали бы переменные свободными. В этом случае удобно искать элементы решения в виде

.

1. Исследование систем уравнений с помощью метода Гаусса

Рассмотрим систему общего вида

Не уменьшая общности, считаем, что Если это не так, то переставим уравнения или перенумеруем неизвестные.

1 этап. Исключаем переменную из уравнений 2-го, … , s-го с помощью первого уравнения. Для этого из – го уравнения вычтем 1 е, умноженное на Получаем систему

Может оказаться, что в левой части одного из полученных уравнений все коэффициенты равны 0. Если при этом правая часть этого уравнения тоже равна 0, то уравнение отбросим. Если же правая часть этого уравнения не равна 0, то делаем вывод, что система является несовместной, прекращаем вычисления.

Предположим, мы отбросили некоторые уравнения, тогда после первого этапа система имеет вид

,

Продолжим процесс исключения неизвестных далее:

k - й этап. Исключаем переменную из уравнений (k+1)-го, …, последнего. При этом считаем, что , в противном случае перенумеруем неизвестные или переставим уравнения. Вычтем из уравнения умноженное на

В процессе вычислений либо некоторые уравнения (имеющие вид ) могут быть отброшены, либо может быть сделан вывод о несовместимости системы (если одно из новых уравнений имеет вид , где ).

Пусть система оказалась совместной. Окончательно придём к системе, имеющей трапециевидную (или ступенчатую) матрицу

Могут быть два случая:

1. ( то есть система имеет треугольную матрицу):

Найдём из последнего уравнения :

Подставим это значение в предыдущее уравнение, найдём . Аналогично найдём . То есть в случае система имеет единственное решение.

. Назовём переменные свободными, присвоим им значения . Для нахождения переменных получаем систему с треугольной невырожденной матрицей ( в процессе решения было зафиксировано, что ).

Найдём , двигаясь по системе снизу вверх так, как это было проделано для случая . Окончательно найдём общее решение системы:

Замечания.

1. Процесс преобразования системы к системе с трапециевидной матрицей называется прямым ходом метода Гаусса. Процесс вычисления неизвестных называется обратным ходом метода Гаусса.

2. Метод Гаусса является точным методом, то есть, если вести вычисления без округлений , то получим точное значение решения. На практике вести вычисления без округлений удаётся редко. Поэтому используются модификации метода Гаусса, позволяющие избежать накопления ошибок округления (например, метод Гаусса с выбором главного элемента).

3. Метод Гаусса преобразования квадратной матрицы к треугольному виду используется для вычисления определителей:

Элементарные преобразования строк и столбцов

Но . Отсюда , где s – число произведенных перестановок строк и столбцов.

1. Метод элементарных преобразований вычисления ранга матрицы является частным случаем применения метода Гаусса.

2. Метод Гаусса позволяет ответить на вопрос о несовместности системы без использования понятия ранга матрицы ( то есть без применения теоремы Кронекера-Капелли).

Пример. Решим с помощью метода Гаусса систему

Решение. Запишем преобразования системы в виде преобразования её матрицы:

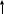
Здесь «старая» k я строка матрицы;

«новая» k я строка матрицы.

Матрица приведена к ступенчатому виду. Переменные считаем свободными: . Выпишем соответствующую систему:

Отсюда , подставим это выражение для в первое уравнение, найдём .

Ответ.

Запишем ответ в матричном виде:

Сравним с формулой (3) общего решения неоднородной СЛАУ, получим, что ;

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов лекций