Методические указания (1114907), страница 4
Текст из файла (страница 4)
α2=*Е β2=i
Е = β1E’/ β2E’
E’= α1E’/ α2E’/ε
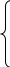 E→ (E)E’
E→ (E)E’
E → iE’
E’ → +EE’
E’ → *EE’
E’ → ε
-
Грамматика является левофакторизованной, потому что не встречается правил вида:
А →аС
А → аD
-
По преобразованной грамматике построим деревья разбора
-
i*(i+i)
-
i*i+i
-
(i+i)*(i+i)
Задача 3 «Построение таблицы предиктивного анализатора»
Теоретическая часть
Определение: Предиктивный анализатор представляет собой программу, содержащую процедуры для каждого нетерминального символа.
Определение: Анализ методом рекурсивного спуска (recursive-descent parsing) представляет собой способ нисходящего синтаксического анализа, при котором выполняется рад рекурсивных процедур для обработки входного потока (процедура связана с каждым нетерминальным символом грамматики).
Определение: Предиктивный анализ – анализ, при котором сканируемый символ однозначно определяет процедуру, выбранную для каждого нетерминала.
При построении предиктивного синтаксического анализатора можно создать его план в виде диаграммы переходов. Для построения диаграммы переходов предиктивного синтаксического анализатора на основе грамматики вначале следует устранить из нее левые рекурсии, а затем провести левую факторизацию. После этого для каждого нетерминала А выполняется следующее.
-
Создаем начальное и заключительное состояния.
-
Для каждой продукции А →Х1Х2…Хn создаем путь от начального к заключительному состоянию с дугами, помеченными как Х1, Х2, …, Хn.
FIRST и FOLLOW
Если α – произвольная строка символов грамматики, то определим FIRST(α) как множество терминалов, с которых начинаются строки, выводимые из α. Если α → ε, то ε € FIRST(α).
Определим FOLLOW(A) для нетерминала А как множество терминалов, которые могут располагаться непосредственно справа от А в некоторой сентенциальной форме, т е множество терминалов а, таких, что существует порождения вида S=>αAaβ для некоторых α и β.
Чтобы вычислить FIRST(X) для всех символов грамматики Х, будем применять следующее правило до тех пор, пока ни к одному из множеств FIRST не смогут быть добавлены ни терминалы, ни ε.
-
Если Х – терминал, то FIRST(X) = {X}.
-
Если имеется продукция Х → ε, добавим ε к FIRST(X).
-
Если Х – нетерминал и имеется продукция Х → Y1Y2…Yk, то поместим а в FIRST(X), если для некоторого i a € FIRST(Yi) и ε входит во все множества FIRST(Y1), …, FIRST(Yi-1), т е Y1 … Yi-1 =>ε. Если ε имеется во всех FIRST(Yi), i=1..k, то добавляем ε к FIRST(X).
Теперь можно вычислить FIRST для любой строки Х1Х2… Хn следующим образом. Добавим к FIRST(Х1Х2… Хn) все не-ε символы из FIRST(Х1). Добавим также все не-ε символы из FIRST(Х2), если ε € FIRST(Х1), все не-ε символы из FIRST(Х3), если ε имеется как в FIRST(Х1), так и в FIRST(Х2) и т д. Добавим FIRST(Х1Х2… Хn), если для всех i FIRST(Хi) содержит ε.
Чтобы вычислить FOLLOW(A) для всех нетерминалов А, будем применять следующие правила до тех пор, пока ни к одному множеству FOLLOW нельзя будет добавить ни одного символа.
-
Поместим $ в FOLLOW(S), где S – стартовый символ, а $ - правый ограничитель входного потока.
-
Если имеется продукция А → αВβ, то все элементы множества FIRST(β), кроме ε помещаются в множество FOLLOW(В).
-
Если имеется продукция А → αВ или А →αВβ, где FIRST(β) содержит ε, то все элементы из множества FOLLOW(А) помещаются в множество FOLLOW(В).
Для построения таблицы предиктивного анализа данной грамматики G может использоваться приведенный далее алгоритм. Идея алгоритма в следующем. Предположим, что А → α представляет собой продукцию, у которой а € FIRST(α). Тогда синтаксический анализатор заменит А строкой α при текущем входном символе а. Единственная сложность возникает при α=ε или α=>ε. В этом случае мы снова должны заменить А на а, если текущий входной символ имеется в FOLLOW(А) или из входного потока получен $, который входит в FOLLOW(А).
Алгоритм «Построение таблицы предиктивного анализатора»
Вход. Грамматика G.
Выход. Таблица анализа М.
Метод.
-
Для каждой продукции грамматики А → α выполняем шаги 2 и 3.
-
Для каждого терминала а из FIRST(α) добавляем А → α в ячейку М[A,a].
-
Если в FIRST(α) входит ε, для каждого терминала b из FOLLOW(А) добавим А → α в ячейку М[A,b]. Если ε входит в FIRST(α), а $ - в FOLLOW(А), добавим А → α в ячейку М[A,$].
-
Сделаем каждую неопределенную ячейку таблицы М указывающей на ошибку.
Восстановление после ошибок
Правила восстановления после ошибок в «режиме паники»:
-
В качестве первого приближения можем поместить в синхронизирующее множество для нетерминала А все символы из множества FOLLOW(A). Если пропустим все токены до элемента из FOLLOW(A) и снимем А со стека, вероятно, мы сможем продолжить синтаксический анализ.
-
В качестве синхронизирующего множества для А недостаточно использовать FOLLOW(A). К синхронизирующему множеству конструкций нижнего уровня можно добавить символы, с которых начинаются конструкции более высокого уровня.
-
Если мы добавим символы из FIRST(A) в синхронизирующее множество для нетерминала А, станет возможным продолжение анализа в соответствии с А, когда во входном потоке появится символ из множества FIRST(A).
-
Если нетерминал может порождать пустую строку, то в качестве продукции по умолчанию в качестве продукции может использоваться, порождающая ε. Это может отсрочить обнаружение ошибки, зато не может вызвать ее пропуск, и сокращает число нетерминалов, которые должны быть рассмотрены в процессе восстановления после ошибки.
-
Если терминал на вершине стека не может быть сопоставлен с входным символом, то простейший метод состоит в снятии терминала со стека, генерации сообщения о вставке терминала в программу и продолжении синтаксического анализа.
Условие:
-
По описанию языка построить КС-грамматику.
-
Определить свойства полученной грамматики.
-
Если грамматика не обладает свойствами, требуемыми для построения таблицы предиктивного анализатора, то преобразовать грамматику к требуемой форме.
-
Определить значение функций FIRST и FOLLOW для разработанной грамматики.
-
Построить таблицу предиктивного анализатора.
-
Проверить правильность построения на трех примерах (один правильный, два неправильных).
Варианты:
| № | Формулировка варианта задания |
| | <E> ::= <E> ‘+’ <E> | <E> ‘*’ <E> | ‘(‘ <E> ‘)’ | ‘i’ |
| | <S> ::= ‘if’ <E> ‘then’ <O> [ ‘else’ <O> ] <E> ::= ‘i’ | ‘i’ ‘==’ <E> <O> ::= ‘o’ … |
| | type: formalParameter: block: |
| | |
| | <P> ::= [ <H> ] <B> <H> ::= ‘h’ (‘t’ ‘i’)… <B> ::= ‘b’ (‘,’ ‘b’)… ‘;’ |
| | <P> ::= <H> [ <B> ] <H> ::= ‘h’ (‘t’ ‘i’)… <B> ::= ‘b’ (‘,’ ‘b’)… ‘;’ |
| | <P> ::= [ <H> ] [ <B> ] <H> ::= ‘h’ (‘t’ ‘i’)… <B> ::= ‘b’ (‘,’ ‘b’)… ‘;’ |
| | <P> ::= <H> (<B>)… <H> ::= ‘h’ (‘t’ ‘i’)… <B> ::= ‘b’ (‘,’ ‘b’)… ‘;’ |
| | <P> ::= [ <H> ] <B> <H> ::= ‘h’ (‘t’ ‘i’)… <B> ::= ‘b’ (‘,’ ‘b’)… [‘;’] |
| | <P> ::= [ <H> ] <B> <H> ::= [‘h’] (‘t’ ‘i’)… <B> ::= ‘b’ (‘,’ ‘b’)… [‘;’] |
| | <P> ::= <H> [ <B> ] <H> ::= [‘h’] (‘t’ ‘i’)… <B> ::= ‘b’ ( [ ‘,’ ] ‘b’)… ‘;’ |
| | <P> ::= <H>… [ <B> ] <H> ::= [‘h’] (‘t’ ‘i’)… <B> ::= ‘b’ ( [ ‘,’ ] ‘b’)… [ ‘;’ ] |
| | <P> ::= <H> [ <B>… ] <H> ::= [‘h’] (‘t’ ‘i’)… <B> ::= [‘b’] ( [‘,’] ‘b’)… ‘;’ |
| | <P> ::= ([ <H> ] [ <B> ])… <H> ::= ‘h’ (‘t’ ‘i’)… <B> ::= ‘b’ (‘,’ ‘b’)… ‘;’ |
| | <P> ::= (<H> | <B>)… <H> ::= ‘h’ (‘t’ ‘i’)… <B> ::= ‘b’ (‘,’ ‘b’)… ‘;’ |
| | <P> ::= <H> [ <B> ] <H> ::= ‘h’ (‘t’ ‘i’)… | ε <B> ::= ‘b’ (‘,’ ‘b’)… ‘;’ |
| | <E> ::= <E> ‘-’ <E> | <E> ‘+’ <E> | ‘(‘ <E> ‘)’ | ‘i’ |
| | <S> ::= ‘if’ <E> ‘then’ <O> [ ‘else’ <O> ] <E> ::= ‘i’ | ‘i’ ‘<>’ <E> <O> ::= ‘o’ <O> | <S> | ‘o’ |
| | |
| | b: |
| | h: b: |
| | h: b: |
| | h: b: |
| | <S> ::= ‘if’ [ <E> ] ( [ ‘i’ ‘:’ ] ‘then’ <O> )… <E> ::= ‘i’ | ‘i’ ‘<>’ <E> <O> ::= ‘o’ <O> | <S> | ‘o’ |
| | <S> ::= ‘if’ [ <E> ] ( ‘i’ ‘:’ ‘then’ <O> )… <E> ::= ‘i’ | ‘i’ ‘<>’ <E> <O> ::= ‘o’ <O> | ‘o’ |
| | <S> ::= ‘if’ [ <E> ] ( ‘i’ ‘:’ ‘then’ <O> )… <E> ::= ‘i’ | ‘i’ ‘<>’ <E> <O> ::= ‘o’ <O> | <S> | ‘o’ |
| | <S> ::= ‘if’ [ <E> ] ‘then’ <O> | <O> <E> ::= ‘i’ | ‘i’ ‘<>’ <E> <O> ::= ‘o’ <O> | <S> | ‘o’ |
| | <S> ::= ‘if’ [ <E> ] ‘then’ <O> [ ‘else’ <O> ] | <O> <E> ::= ‘i’ | ‘i’ ‘<>’ <E> <O> ::= ‘o’ <O> | <S> | ‘o’ |
| | <S> ::= ‘if’ [ <E> ] ‘then’ <O> [ ‘else’ <O> ] <E> ::= ‘i’ | ‘i’ ‘<>’ <E> <O> ::= ‘o’ <O> | <S> | ‘o’ |
| | <E> ::= <E> ‘*’ <E> | <E> ‘=’ <E> | ‘(‘ <E> ‘)’ | ‘i’ |
Пример построения таблицы предиктивного анализатора:
-
Дано описание языка: <E> ::= <E> ‘+’ <E> | <E> ‘*’ <E> | ‘(‘ <E> ‘)’ | ‘i’
-
По описанию языка построили КС-грамматику:
-
Полученная грамматика является леворекурсивной и левофакторизованной. Преобразуем грамматику к требуемой форме.
α1=+Е β1=(Е)































