Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 9)

Уравнение (1) является обыкновенным линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Его решением будет:

или , (3)

где А - амплитуда колебаний, т. е. наибольшее отклонение колеблющегося грузика от положения равновесия; оно задается начальными условиями при однократном приложении силы.

Поскольку значения как cos так и sin через 2 радиан повторяются, то можно найти связь между периодом Т₀ и , откуда

(4)

- называется собственной круговой частотой. Она равна числу полных колебаний за секунд. Для вращательного движения круговая частота и величина угловой скорости совпадают.

В

Рис. 2

ыражение в скобках (3) называют фазой колебания. Она определяет смещение в данный момент времени t; – начальная фаза. Она характеризует смещение в начальный момент времени t = 0 и определяется начальными условиями, как и амплитуда А.

П

Рис. 2

усть , тогда .

График этого уравнения приведен на рис. 2. Из (2) и (4) следует, что период колебания не зависит от амплитуды колебаний А.

Скорость (5)

пропорциональна амплитуде и круговой частоте, и отличается по фазе от смещения (3) на . Максимальная скорость .

Ускорение (6)

пропорционально A и , и по направлению совпадает с направлением силы , а по фазе отличается от скорости (6) на , и от смещения (3) – на . Максимальное ускорение .

Простейшее периодическое колебание, при котором смещение изменяется со временем по закону cos или sin называется гармоническим колебанием.

Как следует из (5) и (6) скорость и ускорение колеблющегося груза изменяется со временем также по гармоническому закону, т. е. по закону sin и cos.

2. Потенциальная и кинетическая энергии

Установим изменение потенциальной и кинетической энергий колеблющейся системы. Известно, что потенциальная энергия упруго деформированного тела равна , где k - коэффициент упругости, х - смещение; откуда для потенциальной энергии колебаний находим

. (7)

Кинетическая энергия , что, согласно (2) и (5), в нашем случае будет

. (8)

Анализ (7) и (8) показывает, что когда одна из энергий или увеличивается, то другая уменьшается. Полная же энергия

E=W_n+W_k=kA²/2 (9)

остается величиной постоянной и для пружинного маятника, (см. рис. 1), она определяется работой, совершенной внешней силой по сжатию или растяжению пружины. Итак, мы рассмотрели свободные или собственные колебания, которые происходят в системе, предоставленной самой себе, после того, как она была выведена из положения равновесия.

Но в реальных условиях всегда на механические системы действуют силы трения из-за чего свободные колебания переходят в затухающие, которые будут рассмотрены в параграфе 8.

3. Векторная диаграмма гармонического колебания

Гармоническое колебание

можно представить в виде проекции вектора , вращающегося против хода часовой стрелки с угловой скоростью, равной круговой частоте . Из рис. 3 следует, что проекция вектора на направление ОХ будет .

4. Комплексная форма представления колебаний

С огласно формуле Эйлера для комплексных чисел

, где .

Поэтому уравнение гармонического колебания (3) можно записать в экспоненциальной форме:

Рис. 3

.

Вещественная часть представляет собой смещение х при гармоническом колебании .

Обычно обозначение опускают и пишут так

.

5. Сложение одинаково направленных колебаний

Рассмотрим сложение двух гармонических колебаний одинаковой частоты, смещения которых и .

Используем векторную диаграмму, рис. 4; откуда следует, что где

Рис. 4

.

Пусть , тогда

, т.е. результирующее колебание не будет гармоническим. Если колебания мало отличаются по частоте, например, , , то результирующее колебание можно рассматривать как почти гармоническое колебание с частотой и медленно меняющейся амплитудой . Такие периодические изменения амплитуды называются биениями.

6

Рис. 4

Рис. 5

Рис. 6

. Сложение взаимно перпендикулярных колебаний

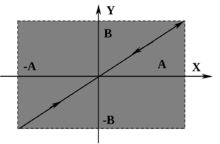
6.1. Пусть и , тогда траекторией будет прямая линия, рис. 5: .

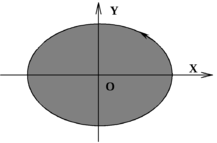
6.2. При и , траекторией будет эллипс, ( рис. 6):

(x²/A²)+(y²/B²)=1.

При разных частотах складывающихся колебаний результирующие траектории будут иметь более сложный вид.

Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу.

7. Гармонические осцилляторы

7.1. Математический маятник

Э то материальная точка, подвешенная на невесомой, нерастяжимой нити.

Хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити, рис. 7. Тангенциальное ускорение а, возникает под действием тангенциальной силы . Для малых можно положить и .

С

Рис. 7

другой стороны тангенциальное ускорение связано с угловым соотношением: .

Из второго закона Ньютона следует, что , или .

Деля правую и левую части этого уравнения на l, получим:

, (10)

где . Решением его для малых φ будет:

, (11)

где

. (12)

Таким образом, период колебаний математического маятника T₀, не зависит от его массы и амплитуды колебаний. Измерения T₀ дают возможность с большой точностью определять g , что позволяет проводить гравитометрическую разведку и определять форму фигуры планеты.

Математический маятник сыграл большую роль в открытии закона сохранения энергии и в создании общей теории относительности, основным положением которой является равенство массы гравитационной и инертной.

7.2. Пружинный маятник

Это груз массой т , подвешенный на абсолютно упругой пружине и совершающий колебания около положения равновесия, рис. 1. Он был рассмотрен в параграфе 1. Для него и (13)

7 .3. Физический маятник

Э

Рис. 8

то твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс С тела. На маятник, отклоненный на малый угол φ действует момент силы , который сообщает угловое ускорение , где J - момент инерции тела, относительно оси, проходящей через точку О перпендикулярно рисунку.

С учетом этого получается дифференциальное уравнение . Разделив правую и левую части последнего уравнения на момент инерции тела J, найдем: ,

где . (14)

Решением его будет .

Период колебания , (15)

где L = J/ml - приведенная длина физического маятника; L - это длина такого математического маятника, период колебаний которого совпадает с периодом колебания данного физического маятника.

Точка О' , расположенная на расстоянии L от точки О (рис. 8), через которую проходит ось подвеса физического маятника, называется его центром качаний. Периоды колебаний относительно точек О и О' совпадают.

8. Свободные затухающие колебания

Кроме силы упругости F = - kx на тело действуют также сила сопротивления, которая при медленных движениях пропорциональна скорости, т. е. , где r - коэффициент сопротивления, с размерностью [r] = кг/с.

С учетом сказанного, уравнение движения тела ( 2-й закон Ньютона ) ma=F будет иметь вид , или, разделив на массу т правую и левую части такого уравнения, имеем :

Рис. 9

, (16)

г де - коэффициент затухания; . Его решение будет

Рис. 10

. (17)

Анализируя (17), можно видеть, что:

1) при ,

т.е. движение получается непериодическим, рис. 9; его называют апериодическим, т.к. тело монотонно стремится к положению равновесия.

2) при (18)

где - амплитуда, а

. (19)

Из (19) следует, что затухающие колебания не являются строго гармоническими, их амплитуда A(t), уменьшается с течением времени и тем быстрее, чем больше коэффициент затухания (рис. 10).

8.1. Логарифмический декремент затухания

Натуральный логарифм отношения отклонения системы в моменты времени t и называется логарифмическим декрементом затухания:

.(20)

Величина, обратная , показывает число колебаний, совершаемых за время, в течение которого амплитуда колебаний уменьшается в е = 2,7182 раз.

Величина (21)

называется добротностью колебательной системы.

Заметим, что рассмотренная колебательная система является диссипативной, т.к. ее механическая энергия постепенно уменьшается с течением времени за счет преобразования в другие (немеханические) формы энергии.

9. Вынужденные колебания

Они возникают при действии на систему внешней периодически изменяющейся силы (вынуждающей силы) , (22)

где - круговая частота вынуждающей силы.

Дифференциальное уравнение вынужденных колебаний с учетом затухания запишется в виде:

m(d²x/dt²) = -kx - r(dx/dt) + F_mcos t.

Перепишем это уравнение в виде:

. (23)

Таким образом, получили линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решением такого уравнения будет , где – общее решение однородного уравнения (23), (т. е. уравнения (23) с правой частью, равной нулю). Согласно (17)

и с течением времени . Поэтому .

Из решения (23) следует, что (24)

где , (25)

. (26)

И з анализа (25) следует, что хотя амплитуда вынуждающей силы F_m, остается постоянной, амплитуда А вынужденных колебаний зависит от частоты вынуждающей силы.

Исследуя (25) на экстремум, можно показать, что только при резонансной частоте

Рис. 11

(27)

амплитуда вынужденных колебаний достигает максимальной величины: . (28)

Это явление называется резонансом.

На рис. 11 приведена зависимость амплитуды А вынужденных колебаний от частоты вынуждающей силы , которая определяется формулой (25); (откуда: при = 0 находим , а при имеем , что объясняется инерционностью колебательной системы).

Явление резонанса, состоящее в резком увеличении амплитуды колебаний при приближении частоты вынуждающей силы к резонансной частоте, широко используется в технике. Его следует учитывать при конструировании машин, кораблей, самолетов и т.д. Необходимо, чтобы их резонансные частоты не совпадали с частотой вынуждающих внешних воздействий.

При написании конспекта лекций использовались известные учебники по физике, изданные в период с 1923 г. (Хвольсон О. Д. «Курс физики») до наших дней (Детлаф А. А., Яворский Б. М., Савельев И. В., Сивухин Д. В., Трофимова Т. И., Суханов А. Д. и др.).

Характеристики

Список файлов лекций