Тонкостенные купола

56. Тонкостенные купола – оболочки из древесины и пластмасс. Основные принципы конструктивного выполнения и расчета

Тонкостенные купола-оболочки

По характеру работы к этой конструктивной схеме ближе всего относятся пластмассовые гладкие купола-оболочки однослойные, двух- и трехслойные. Однослой­ные пластмассовые купола изготовляют из полиметилме-такрилата (органическое стекло), полиэфирного стекло­пластика (чаще всего светопрозрачного) и пенопласта (пенополистирол и др.). Трехслойные купола-оболочки сбщей толщиной от 15 до 50 мм имеют стеклопластико-вые обшивки толщиной до 3 мм и средний слой из пено-полистирола, пенополиуретана, пенополивинилхлорида, пенофенопласта, сотопласта и просто воздушной про­слойки. Двухслойные оболочки состоят из наружного стеклопластикового слоя и внутреннего пенопластового.

Диаметр и толщина однослойных куполов из полиметилметакрилата соответственно достигают 10 м и 20 мм; из стеклопластика—9 м и 6 мм; из пенопласта—24 м и 200 мм. Трехслойные купола возводят диаметром до 25 м с общей толщиной оболочки до 50 мм.

Параметры двухслойных куполов аналогичны одно­слойным стеклопластиковым, так как внутренний пено­пластовый слой в основном выполняет функцию утепли­теля.

Интересным примером трехслойного пластмассового купола является покрытие выставочного павильона в г. Бергамо (Италия) (рис. 1). Диаметр купола 25 м, высота подъема 9 м, общая толщина оболочки 50 мм, обшивка из стеклопластика толщиной 3 мм, средний слой — пенопласт. Купол собран на болтах из 24 одно­типных сегментов с размером понизу около 3,3 м, имею­щих круглые проемы диаметром 1 м, заполненные акри­ловыми фонарями. Сегменты опираются на полое желе­зобетонное кольцо с размещенным на нем техническим оборудованием. С двух сторон по диаметру купола устрое­ны крупногабаритные проемы для въезда грузовых авто­мобилей. При необходимости можно стыковать несколь­ко куполов по выступам входного обрамления проемов, получив тем самым многокупольное помещение. Масса покрытия на 1 м² перекрываемой площади 20 кг.

Деревянные тонкостенные купола-оболочки проекти­руют диаметром 12—35 м; они, как правило, имеют сфе­рическое очертание. Купол состоит (рис. 2) из ме­ридианных ребер (арочек), верхнего и нижнего опорных колец, кольцевого и косого настилов.

Меридианные ребра воспринимают сжимающие уси­лия в оболочке по направлению меридиана и передают их на верхние и нижние опорные кольца. Ребра состоят из нескольких слоев склеенных или сбитых гвоздями до­сок, общей высотой поперечного сечения не менее 1/250 диаметра купола, которую принимают из условия его жесткости. Шаг ребер по нижнему опорному кольцу на­значают 0,8—1,5 м. Верхние концы ребер присоединяют шарнирно к верхнему сжатому кольцу. Ребра передают на кольцо продольную и поперечную силу. Соединения осуществляют металлическими накладками, присоединяемыми к ребрам болтами, глухарями или зубчатыми шпонками. При значительных поперечных усилиях при­меняют сварные металлические башмаки.

Верхнее кольцо изготовляют металлическим или де­ревянным. Деревянные кольца могут быть клееными или кружальными на гвоздях. Диаметр верхнего кольца при­нимают таким, чтобы к нему беспрепятственно примыка­ло требуемое количество меридианных ребер. Отверстие кольца часто используют как световой или аэрационный фонарь.

Рекомендуемые материалы

Нижнее опорное кольцо воспринимает распор мери­дианных ребер и работает на растяжение. Оно может быть железобетонным, деревянным или металлическим в зависимости от уровня опирания купола и вида ниж­них опорных конструкций (железобетонные фундаменты, металлические или деревянные стойки и т. д.). Концы ребер должны быть заанкерены в опорном кольце, а по­следнее надежно соединено с нижележащими конструк­циями.

Кольцевые настилы воспринимают усилия, действую­щие в кольцевом направлении оболочки. В нижней части купола, где могут возникать растягивающие кольцевые усилия, кольцевой настил выполняют из двух слоев до­сок. Нижний укладывают непосредственно на меридиан­ные ребра, верхний — перекрывает стыки нижнего, сдви­гаясь относительно их на половину длины доски. Оба слоя прибивают гвоздями. Доски не выкружаливают и поэтому между ними образуются зазоры. Вместо досок можно применять склеенные по длине плети брусков. В этом случае настил может быть одинарным, стыки пле­тей располагаются вразбежку и соединяются гвоздями через меридианное ребро иди смежные бруски. Толщину досок кольцевого настила принимают 19—25 мм. В верх­ней части купола, где действуют сжимающие кольцевые усилия, настил выполняют из одного слоя досок (брус­ков) толщиной, равной двойному нижнему кольцевому настилу.

Рис.2 Тонкостенный купол-оболочка

а — поперечный разрез и план; б — примыкание к верхнему опорному кольцу; в — детали покрытия; г — примылание к нижнему опорному кольцу; / — до­щатые ребра; 2 — нижний слой кольцевого настила; 3—верхний слой коль­цевого настила; 4 — косой настил; 5 — кровля; 6 — верхнее опорное кольцо; 7 — нижнее железобетонное опорное кольцо; 8 — фонарь; 9 — металлическая деталь крепления ребер

Косой настил воспринимает сдвигающие усилия, ко­торые возникают при несимметричной нагрузке на купол. Он состоит из одного слоя досок толщиной 16—25 мм, укладываемого сверху кольцевого настила от одного ме­ридианного ребра к другому, под углом около 45°, обра­зуя на поверхности купола елочку.

Купола-оболочки могут быть выполнены из крупно­панельных клеефанерных элементов, что значительно снижает трудоемкость возведения покрытия.

Деревянные тонкостенные купола-оболочки собирают с помощью лесов. Особое внимание обращается на приторцовку стыков сжатого кольцевого настила.

Статический расчет куполов-оболочек производят по безмоментной теории, согласно которой для сферической оболочки при действии на нее осесимметричной нагрузки основное уравнение напряженного состояния имеет вид

T₁ + T₂ = qR,

где T₁ — меридиональное усилие на единицу длины кольцевого се­чения; T₂ — кольцевое усилие на единицу длины дуги меридиана; q — равномерно распределенное нормальное к поверхности купола давление, направленное к центру сферы; R — радиус сферического купола (рис. 3,а).

Определение усилий от собственного веса. Постоян­ная нагрузка от собственного веса g считается равно­мерно распределенной по всей поверхности купола (рис. 3, а). Для определения меридионального уси­лия ti рассмотрим равновесие верхней части купола, отсеченной горизонтальной плоскостью, проходящей на расстоянии у от центра сферы (рис. 3, а). На отсе­ченный сферический сегмент действует нагрузка от соб­ственного веса вышележащей части купола

2pRfg = 2pR (R - R Сosj)×g,

которая уравновешивается проекцией на вертикальную ось меридиональных усилий T₁, действующих по перимет­ру кольцевого сечения радиусом r = R Sinj,

Т₁2pr sinj = Т₁2pR sin²j,

отсюда меридиональное усилие на единицу длины коль­ца равно

.

Рис.3 Нагрузки и усилия в куполе-оболочке

а — расчетная схема; б — эпюры меридиональных и кольцевых усилий от соб­ственного веса купола; в — то же, от снеговой нагрузки; г, е — эпюры ветро­вого давления на купол в поперечном сечении и в плане; д, ж — симметрич­ная и кососимметричная эпюры ветрового давления на купол

Для тонкостенного деревянного купола-оболочки при числе меридианных ребер m и расстоянии между ними по длине дуги рассматриваемого горизонтального сече­ния а усилие в одном ребре в данном горизонтальном се­чении определяется:

T_1реб = T₁а.

Кольцевое усилие Т₂ найдем из основного уравнения без­моментной сферической оболочки

откуда кольцевое усилие на единицу длины меридиана

При угле ф = 51°49' кольцевое усилие меняет свой знак, переходя от сжимающего к растягивающему.

Усилия Т₁ и Т₂, справедливы для сплошного замкнутого купола. Если в куполе имеется фонарное отверстие и масса фо­наря более чем в 1,5 раза отличается от массы вырезан­ной части купола, то необходимо учесть нагрузку Р_к (рис. 3, а), линейно распределенную по краю сечения фонарного выреза

T₁ = - P_к(Sinj₁/ Sin²j);

T₁ = P_к(Sinj₁/ Sin²j).

Растягивающие усилия в опорном кольце от собст­венного веса купола можно определить по формуле

N_к = Q_jo/2p×tgj₀.

где Q_jo - масса купола.

Q_jo = 2pR²g(1 - Cosj₀).

Для случая кольцевой нагрузки по фонарному вырезу

N_к = P_кR×Sinj₁×ctgj₀.

Определение усилий от снеговой нагрузки. Интенсив­ность снеговой нагрузки по поверхности купола обычно принимают по закону косинуса Р = Р₀Cоsj, где Р₀ — равномерно распределенная нагрузка по проекции по­верхности на горизонтальную плоскость.

Меридиональное усилие на единицу длины кольца в любом сечении имеет постоянное значение

Усилие на одно меридианное ребро составит

Кольцевое усилие на единицу длины меридиана опре­делится с учетом нормальной составляющей нагрузки в уровне кольцевого сечения q = P₀Cos²j

Кольцевое усилие меняет знак при j = 45°. Усилие растяжения в опорном кольце

N_к = (P₀R²/4)Sin2j₀.

При действии на купол несимметричной нагрузки в оболочке кроме меридиональных и кольцевых усилий возникают сдвигающие усилия S. Расчет сферического купола на одностороннюю снеговую нагрузку, исходя из нормальной к поверхности купола нагрузки

P = 0,4P₀(1 + Sinj×Siny),

где P₀ — нагрузка на единицу площади горизонтальной поверхности; y - угол широты в плане нижнего круга сферического купола, от­считываемый от диаметра, перпендикулярного направлению ветра, при котором получается одностороннее загружение (рис. 3, е).

Определение усилий от ветровой нагрузки произво­дят приближенно заменой действительной эпюры ветро­вого давления (рис. 3, г) суммой двух эпюр — сим­метричной (рис. 3, д) , где  - рас­четная нагрузка от давления ветра на вертикальную плоскость на уровне основания купола, и кососимметричной (рис. 3, ж) .

Усилия от симметричной эпюры:

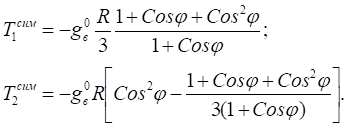
Усилия от кососимметричной эпюры ветрового давле­ния:

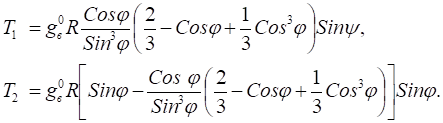
Купольные покрытия обладают хорошей обтекае­мостью. Поэтому при f/l £ 1/4 достаточно учесть только симметричный отсос. Для купола с f/l >1/4 следует принимать во внимание и кососимметричную ветровую на­грузку.

Усилие сжатия в кольце

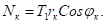
Проверка кольца на устойчивость

Люди также интересуются этой лекцией: 15 Способы обнаружения, фиксации и изъятия огнестрельного оружия, пуль и гильз, обнаруженных на месте происшествия.

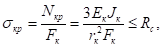
где F_к, E_к, J_к, г_к - площадь поперечного сечения, модуль упругости материала, момент инерции и радиус кривизны кольца относительно вертикальной оси.

Критическое напряжение потери устойчивости сфери­ческой оболочки проверяют по формуле

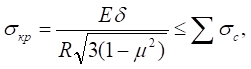
где d - толщина оболочки; E, m - модуль упругости и коэффициент Пуассона материала (древесины, пластмасс, фанеры); Ss_c - сум­марное сжимающее напряжение от всех видов загружения; R - ра­диус кривизны сферической оболочки.

Сдвигающие усилия в сферическом куполе при кососимметричной ветровой нагрузке