Целочисленное программирование
5.Лекция. Целочисленное программирование.
5. 1 Постановка задачи целочисленного программирования.
В ряде экономических задач, относящихся к задачам линейного программирования, элементы решения должны выражаться в целых числах. В этих задачах переменные означают количество единиц неделимой продукции.
Задача целочисленного программирования формулируется следующим образом:
Найти такое решение план Х=(х1, х2,…, хn), при котором линейная функция  принимает максимальное или минимальное значение при ограничениях
принимает максимальное или минимальное значение при ограничениях

задача решается методами линейного программирования. В случае если переменные оптимального решения оказываются нецелочисленными, то, применяя методы отсечения или метод перебора целочисленных решений.
Понятия о методе ветвей и границ.
Метод ветвей и границ заключается в упорядоченном переборе вариантов и рассмотрении лишь тех из них, которые оказываются по определенным признакам перспективными, и отбрасывании бесперспективных вариантов.
Рекомендуемые материалы
Метод ветвей и границ состоит в следующем: множество допустимых решений (планов) некоторым способом разбивается на подмножества, каждое из которых этим же способом снова разбивается на подмножества. Процесс продолжается до тех пор. Пока не получено оптимальное целочисленное решение исходной задачи.
Название метода ветвей и границ исходит из того, что в процессе решения задача последовательно «ветвится», заменяясь более простыми. Процесс решения можно продолжать в виде дерева, цифры в узлах (вершинах) которого обозначают план решения задачи (искомые переменные).
5.2 Графический метод решения задач целочисленного программирования.
При наличии в задаче линейного программирования двух переменных, а в системе ограничения – неравенств, она может быть решена графическим методом без требований целочисленных переменных.
Если оптимальное решение этой задачи является целочисленным, то оно и является оптимальным для исходной задачи.
Если же полученное оптимальное решение не целочисленное, то строится дополнительное линейное ограничение. Оно обладает следующими свойствами:
1.Оно должно быть линейным;
2.Должно отсекать найденный оптимальный не целочисленный план;
3.Не должно отсекать ни одного целочисленного плана.
Алгоритм графического решения задачи целочисленного программирования.
1.Построить систему координат x10х2 и выбрать масштаб.
2.Найти область допустимых решений (ОДР) системы ограничений задачи.
3.Построить целевую функцию, являющуюся линией уровня и на ней указать направление нормали.
4.Переместить линию целевой функции по направлению нормали через ОДР, чтобы она из секущей стала касательной к ОДР и проходила через наиболее удаленную от начала координат точку. Эта точка будет являться точкой экстремума, т.е. решением задачи.
Если окажется, что линия целевой функции параллельна одной из сторон ОДР, то в этом случае экстремум достигается во всех точках соответствующей стороны, а задача линейного программирования будет иметь бесчисленное множество решений.
5.Найти координаты, точки экстремума и значение целевой функции в ней. Если полученные значения не целочисленные, то перейти к следующему шагу.
6.Выделить у этих координат область с целочисленными значениями.
7.Определить новые координаты и построить граф.
8.Найти точки с целыми значениями искомых переменных, подставить в уравнение целевой функции и найти её значение. Максимальное из полученных значений целевой функции и будет решением задачи.
1.3 Пример решения задачи целочисленного программирования.
Условие задачи.
Решить методом ветвей и границ задачу, имеющую следующую математическую модель.

Решение:
1.Находим координаты точек каждого линейного уравнения системы ограничений и строим прямые
1 прямая: 3х1+2х2=1
-если х1=1, то 2х2=12, х2=6
-если х2= 0, то 3х1=12, х1=4
2 прямая: 2х1+5х2=20
-если х1=0, то 5х2=20, х2=4;
-если х2=0, то 2х1=20, х1=10
2.Находим ОДР.
Так как х1, х2 ≥ 0, то область будет ограничен прямыми ОХ1 и ОХ2 и построенными прямыми (см. рис.1).
3.Находим координаты точек целевой функции и строим прямую целевой функции:
7х1+4х2=0
- первая точка х1=0; х2=0
- вторая точка х1=4, х2=(-7).
4.Перемещаем прямую целевой функции по направлению через ОДР до тех пор, пока она не станет касательной к ней, и находим точку А0.
5.Находим координаты точек А0 и значение целевой функции в ней:
Х1=1,8; х2=3,27;
Z=7×1,8+4×3,27=12,6+13,08=25,68
Получен не целочисленный оптимальный план
6.выделим область относительно точки А0 беря целые значения 1 ≤ х1 ≤ 2; 3 ≤ х2 ≤ 4.
Получим координаты точек по границе этой области:
А1 (1;3,6) А2 (2;3); А3 (0;4); А4 (1;3); А5 (0;3); А6 (1;0); А7 (2;0).
7.Строим граф (рис.2)
8.Для точек с целыми значениями их координат (искомые значения х1 и х2)находим значения целевой функции:
Для точки А2 (2;3) Z2= 7×2+4×3=26
Для точки А3 (0;4) Z3= 7×0+4×4=16
Для точки А4 (1;3) Z4= 7×1+4×3=19
Для точки А5 (0;3) Z5= 7×0+4×3=12
Для точки А6 (1;0) Z6= 7×1+4×0=7
Для точки А7 (2;0) Z7= 7×2+4×0=14
Так как максимальное значение целевой функции находится для точки А2 (2;3), то она и будет оптимальным целочисленным решением задачи.
Ответ: Z=26; х1=2; х2=3.


5.4. Задача коммивояжера.
Имеется необходимость посетить n городов в ходе деловой поездки. Спланировать поездку нужно так, чтобы, переезжая из города в город, побывать в каждом не более одного раза и вернуться в исходный город. Определить оптимальный маршрут посещения городов и его минимальное расстояние.
Задана матрица расстояний между городами cij.
Сформулированная задача - задача целочисленная. Пусть хij = 1 , если путешественник переезжает из i -ого города в j-ый и хij = 0, если это не так.
Формально введем (n+1) город, расположенный там же, где и первый город, т.е. расстояния от (n+1) города до любого другого, отличного от первого, равны расстояниям от первого города. При этом, если из первого города можно лишь выйти, то в (n+1) город можно лишь придти.
Введем дополнительные целые переменные, равные номеру посещения этого города на пути. u1 = 0, un+1 = n . Для того, чтобы избежать замкнутых путей, выйти из первого города и вернуться в (n+1) введем дополнительные ограничения, связывающие переменные xij и переменные ui. ( ui целые неотрицательные числа).
2. Математическая модель
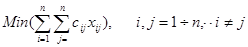
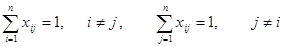
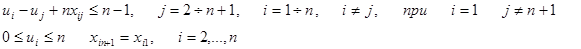
5.5. Пример решения задачи.
Условия задачи:
Необходимо посетить 4 города в ходе деловой поездки Спланировать поездку нужно так, чтобы, переезжая из города в город, побывать в каждом не более одного раза и вернуться в исходный город. Определить оптимальный маршрут посещения городов и его минимальное расстояние.
Матрица расстояний cij между городами задана таблицей:
| Номер города | 1 | 2 | 3 | 4 |
| 1 | 19 | 25 | 11 | |
| 2 | 37 | 26 | 58 | |
| 3 | 10 | 50 | 39 | |
| 4 | 38 | 39 | 24 |
Решение задачи.
Составляем математическую модель задачи.
Zmin=19х12+25х13+11х13+37х21+26х23+58х24+10х31+50х32+39х34+38х41+39х42+24х43
х12+х13+х14=1 х21+х31+х41=1
х21+х23+х24=1 х12+х32+х42=1
х41+х42+х34=1 х13+х23+х43=1
х21+х23+х24=1 х14+х42+х34=1
U1 - U2 + 4х12 < 3
U1 –U3 + 4х13 < 3
U1 – U4+ 4х14 < 3
U2 – U3 + 4х23 < 3
U2 –U4 + 4х24 < 3
U3 – U2+ 4х32 < 3
U3 – U4 + 4х34 < 3
U4 – U2 + 4х42 < 3
U4 –U3 + 4х43 < 3
U4 – U1+ 4х41 < 3
U3 – U1 + 4х31 < 3
U2 –U1 + 4х21 < 3

0,
Хij= - ЦЕЛЫЕ ,
1
где:
Zmin - минимальный маршрут посещения городов;
cij - расстояние между городами ij ;
Ui - номер посещения i – го города.
Строим граф посещения городов с учетом возможных маршрутов движения коммивояжера.
Граф посещения городов:
| 1 |
|
|
| 3 |
|
|
|
3 |
| 4 |
| 2 |
| 4 |
| 3 |
| 2 |
|
|
|
|
| 4 |
| 2 |
| 2 |
| 3 |
| 1 |
| 1 |
| 1 |
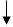




 19
19
25 11
58 50 39 24 39
26
39 24 58 39 50 26




38 10 38 37 37 10
122 111 171 140 122 86
где:
--- расстояние между городами;
--- расстояние, пройденное по маршруту;
"34. Характеристика солончаков, солонцов и солодей." - тут тоже много полезного для Вас.
--- расстояние, пройденное по минимальному маршруту.
| 4 |
Номер города
Ответ:
Минимальный маршрут: 1 --- 4 --- 2 --- 3 --- 1 .
Минимальное расстояние – 86 ед.

 4
4
 4
4 3
3


















