Приближенные методы поиска экстремальных значений функций одной переменной
Тема 7. Приближенные методы поиска экстремальных значений функций одной переменной.
Функция y = f(x) имеет в некоторой окрестности точки x* локальный минимум, если для любой точки x, отстоящей от нее не более чем на некоторую величину e (т.е. | x - x*| < e), справедливо неравенство f(x) < f(x*). Функция y = f(x) имеет в некоторой окрестности точки x** глобальный минимум на некотором интервале [a, b], если для любой точки x из этого интервала (т.е. x Î [a, b]), справедливо неравенство f(x) < f(x**). Точку достижения функцией глобального минимума можно определить посредством выбора из всех точек локальных минимумов или одной из границ интервала той, в которой значение функции будет минимальным. Аналогично можно опредилить локальный и глобальный максимум функции одной независимой переменной. Точки минимума и максимума функции имеют общее название - точки экстремума функции. Ограничимся рассмотрением только дифференцируемых функций.
Необходимым условием наличия в некоторой точке локального экстремума функции является равенство нулю ее производной. Это условие не является достаточным, поэтому такие точки являются только подозрительными на наличие локального экстремума. Достаточным условием наличия в них экстремума является тот факт, что этой точке вторая производная функции будет отличной от нуля (или при переходе через эту точку ее первая производная меняет знак). При этом
· функция имеет минимум, если ее вторая производная в подозрительной на экстремум точке положительна (или в этой точке ее первая производная меняет знак с “+” на “-“)
· функция имеет максимум, если ее вторая производная в подозрительной на экстремум точке отрицательна (или в этой точке ее первая производная меняет знак с “-” на “+“).
Если вторая производная в подозрительной на экстремум точке равна нулю (или в этой точке ее первая производная не меняет знак) - для решения вопроса о наличии в ней экстемума необходимы более сложные исследования.
Поскольку искать корни призводной функции и определять в них знаки вторых ее производных не совсем просто - имеются численные методы приближенного нахождения как глобальных, так и локальных экстремумов функций (с заданной точностью). Для выполнения поиска локальных экстремумов они требуют предварительного выбора интервала такого поиска, т.е. определения границ интервала, внутри которого этот экстремум содержится. А именно,
· для поска локального минимума необходимо выбирать интервал, на котором вторая производная функции знакопостоянная и положительная
Рекомендуемые материалы
· для поска локального максимума необходимо выбирать интервал, на котором вторая производная функции знакопостоянная и отрицательная.
В противных случаях - достаточно проверять конечные точки интервала.
Если вторая производная внутри интервала не является знакопостоянной - применение численных методов затруднено (точне полученный результат может оказаться неверным). Следует также отметить, что задаваемое пользователем значение точности для поиска экстремума тем или иным численным методом должно быть на порядок большим точности вычисления значения функции.
Метод сетки предназначен для поиска глобального экстремума функции на заданном интервале. Суть метода состоит в том, что весь интервал [a, b] покрывается “сеткой” - множеством точек, удаленных друг от друге на более чем на величину заданной точности (e>0), а затем в каждой из этих точек производится расчет значений функции. Далее из них выбирается минимальное (или максимальное), которое (вместе с соответствующей ей абсциссой (т.е. значением переменной x) и будет найденным значением глобального экстремума заданной функции на заданном интервале. Выбор шага разбивки интервала производится так, чтобы выполнялось неравенство  а это возможно при
а это возможно при  .
.
Метод равномерного поиска предназначен для поиска локального экстремума функции на заданном интервале. Суть метода состоит в том, что весь интервал [a, b] аналогичо предыдущему методу покрывается “сеткой” - множеством точек, удаленных друг от друге на более чем на величину заданной точности (e>0), а затем начиная с левого конца заданного интервала (точки x=a) последовательно в каждой из этих точек производится расчет значений функции и сравнение его с расчитанным на предыдущем шаге. Если значения не убывают (при поиске максимума) или не возрастают (при поиске минимума) процесс вычислений повторяют до достижения конца интерваая. Если же тенденция изменения значений нарушается - процесс перебора точек прекращают и предыдущую точку принимают в качестве решения задачи.
Метод последовательного приближения предназначен для поиска локального экстремума функции на заданном интервале. Способ дости-жения цели - в некотором смысле аналогичен ранее описанному методу равномерного поиска. Но имеются два существенных отличия
· шаг поиска (приближения) не является постоянным, а изменяется от некоторого начального значения до значения, меньшего заданной точности (по абсолютной величине) по мере приближения к искомому значению x. Начальное значение шага выбирается равным  , где значение k выбирается таким, чтобы было выполнено двойное неравенство 5 £ k £ 10. В процессе приближения к точке экстремума как знак шага, так и его величина будут изменяться
, где значение k выбирается таким, чтобы было выполнено двойное неравенство 5 £ k £ 10. В процессе приближения к точке экстремума как знак шага, так и его величина будут изменяться
· начиная с левого конца заданного интервала (точки x=a) последовательно в каждой из этих точек производится расчет значений функции и сравнение его с расчитанным на предыдущем шаге. Если значения не убывают (при поиске максимума) или не возрастают (при поиске минимума) процесс вычислений повторяют до достижения конца интервала. Если же тенденция изменения значений нарушается - производят изменение величины и знака шага, полагая
 ,
,
и из последней точки перебор продолжают. Если перед очередной сменой значения шага его абсолютная величина окажеться меньше заданной точности, процесс перебора точек прекращают и предпоследнюю точку принимают в качестве решения задачи.
Процес поиска значения экстремума этим методом удобно проводить с занесением результатов расчетов в таблицу следующего вида
| i | x | f(x) | h |
| 0 | x0=a | h0 | |
| 1 | x1=x0+h | ||
| … | |||
Подробный алгоритм поиска экстремума по этому методу приведен в на рис. 7.1.




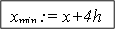





















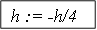
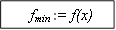






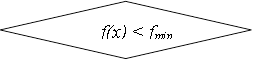


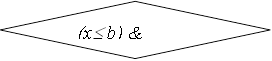

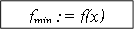

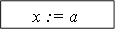



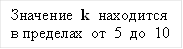














Пример 1. Найти минимум функции  на интервале [0, 5] методом равномерного приближения с точностью 0.025.
на интервале [0, 5] методом равномерного приближения с точностью 0.025.
Имеем  ,
,  . Следовательно, данная функция во всей области ее определения имеет только один локальный (он же и глобальный) минимум. Примем k=5. Тогда h0=1. Дальнейшие вычисления будем проводить в Excel и результаты вычислений представим в виде таблицы.
. Следовательно, данная функция во всей области ее определения имеет только один локальный (он же и глобальный) минимум. Примем k=5. Тогда h0=1. Дальнейшие вычисления будем проводить в Excel и результаты вычислений представим в виде таблицы.
| i | x | f(x) | h |
| 0 | 0,0000 | -5,0000 | 1,0000 |
| 1 | 1,0000 | -10,0000 | 1,0000 |
| 2 | 2,0000 | -13,0000 | 1,0000 |
| 3 | 3,0000 | -14,0000 | 1,0000 |
| 4 | 4,0000 | -13,0000 | -0,2500 |
| 5 | 3,7500 | -13,4375 | -0,2500 |
| 6 | 3,5000 | -13,7500 | -0,2500 |
| 7 | 3,2500 | -13,9375 | -0,2500 |
| 8 | 3,0000 | -14,0000 | -0,2500 |
| 9 | 2,7500 | -13,9375 | 0,0625 |
| 10 | 2,8125 | -13,9648 | 0,0625 |
| 11 | 2,8750 | -13,9844 | 0,0625 |
| 12 | 2,9375 | -13,9961 | 0,0625 |
| 13 | 3,0000 | -14,0000 | 0,0625 |
| 14 | 3,0625 | -13,9961 | -0,0156 |
| 15 | 3,0469 | -13,9978 | -0,0156 |
| 16 | 3,0313 | -13,9990 | -0,0156 |
| 17 | 3,0156 | -13,9998 | -0,0156 |
| 18 | 3,0000 | -14,0000 | -0,0156 |
| 19 | 2,9844 | -13,9998 |
|
Так как на 19-м шаге при очередной смене величины шага его абсолютное значение оказалось меньше заданной точности - процесс приближения прекращен и получены следующие результаты
xmin = 3.000, fmin = -14.000.
Метод дихотомии (другое название - метод половинного деления) предназначен для поиска локального экстремума функции на заданном интервале. Способ достижения цели - в некотором смысле аналогичен ранее описанному методу половинного деления при поиске корней нелинейных уравнений. Исходный отрезок [a, b] делят пополам точкой с с координатой  . После этого находят значения функции в двух пробных точках, находящихся справа и слева от точки с на расстоянии e/2, После этого из двух образовавшихся половинок отрезка одну отбрасывают, а имеено ту, в которой содержится та пробная точка, значение функции в которой меньше (при поиске максимума) или больше (при поиске минимума). Для этого находят значения функции в точках
. После этого находят значения функции в двух пробных точках, находящихся справа и слева от точки с на расстоянии e/2, После этого из двух образовавшихся половинок отрезка одну отбрасывают, а имеено ту, в которой содержится та пробная точка, значение функции в которой меньше (при поиске максимума) или больше (при поиске минимума). Для этого находят значения функции в точках  и
и  , сравнивают их между собой и определяют “отбрасываемую” половину отрезка. Отбрасывание производят посредством переноса в среднюю точку отрезка (точку с) другого конца отбрасываемого отрезка (т.е. точки a или b). Так производят до тех пор, пока длина оставшегося отрезка станет меньшей заданной точности. В таком случае за найденное приближенное значение точки достижения функцией экстремума принимают средину этого (последнего) отрезка.
, сравнивают их между собой и определяют “отбрасываемую” половину отрезка. Отбрасывание производят посредством переноса в среднюю точку отрезка (точку с) другого конца отбрасываемого отрезка (т.е. точки a или b). Так производят до тех пор, пока длина оставшегося отрезка станет меньшей заданной точности. В таком случае за найденное приближенное значение точки достижения функцией экстремума принимают средину этого (последнего) отрезка.
Процес поиска значения экстремума этим методом удобно проводить с занесением результатов расчетов в таблицу следующего вида
| i | a | b | c | ca | f(ca) | cb | f(cb) | b-a |
| 0 |
|
|
|
| ||||
| 1 |
| |||||||
| … |
,
Подробный алгоритм поиска экстремума по этому методу приведен на рис. 7.2.
Пример 2. Найти минимум функции  методом половинного деления с точностью 0.02.
методом половинного деления с точностью 0.02.
Определение интервала поиска обосновано в примере 1, но мы его несколько увеличим для наглядности метода. Решение примера приведем в таблице.
| i | a | b | c | ca | f(ca) | cb | f(cb) | b-a |
| 0 | 0,000 | 7,000 | 3,500 | 3,490 | -13,7599 | 3,510 | -13,7399 | 7,000 |
| 1 | 0,000 | 3,500 | 1,750 | 1,740 | -12,4124 | 1,760 | -12,4624 | 3,500 |
| 2 | 1,750 | 3,500 | 2,625 | 2,615 | -13,8518 | 2,635 | -13,8668 | 1,750 |
| 3 | 2,625 | 3,500 | 3,063 | 3,053 | -13,9972 | 3,073 | -13,9947 | 0,875 |
| 4 | 2,625 | 3,063 | 2,844 | 2,834 | -13,9724 | 2,854 | -13,9786 | 0,438 |
| 5 | 2,844 | 3,063 | 2,953 | 2,943 | -13,9968 | 2,963 | -13,9986 | 0,219 |
| 6 | 2,953 | 3,063 | 3,008 | 2,998 | -14,0000 | 3,018 | -13,9997 | 0,109 |
| 7 | 2,953 | 3,008 | 2,980 | 2,970 | -13,9991 | 2,990 | -13,9999 | 0,055 |
| 8 | 2,980 | 3,008 | 2,994 | 2,984 | -13,9997 | 3,004 | -14,0000 | 0,027 |
| 9 | 2,994 | 3,008 | 3,001 | 2,991 | -13,9999 | 3,011 | -13,9999 | 0,014 |
Ответ - xmin = 3.00, fmin = -14.000.





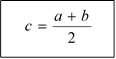























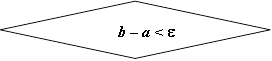








 |
Метод золотого сечения предназначен для поиска локального экстремума функции на заданном интервале. Способ достижения цели - в некотором смысле аналогичен ранее описанному методу дихотомии. Исходный отрезок [a, b] делят на три части точками  и
и  , где l=0.382. Очевидно, что x1 < x2. После этого находят значения функции в крайних точках интервала и в точках x1 и x2. Из четырех полученных значений функции выбирают минимальное (при поиске минимума) или максимальное (при поиске максимума). Дальше производят “отбрасывание” той части интервала (одной из имеющихся трех частей), которая находится наиболее далеко от точки экстремума. Это достигается переносом точки a в точку x1 или точки b в точку x2. В результате проделанных операций длина интервала [a, b] уменьшиться. Теперь к оставшится трем точкам (a, b и x1 или x2) добавим четвертую (недостающий x) по формуле a + b - <имеющийся x > и дальше все повторяем. Так продолжаем до тех пор, пока длина интервала [a, b] не станет меньше заданной точности. В этом случае за точку экстремума примем значение одного из x.
, где l=0.382. Очевидно, что x1 < x2. После этого находят значения функции в крайних точках интервала и в точках x1 и x2. Из четырех полученных значений функции выбирают минимальное (при поиске минимума) или максимальное (при поиске максимума). Дальше производят “отбрасывание” той части интервала (одной из имеющихся трех частей), которая находится наиболее далеко от точки экстремума. Это достигается переносом точки a в точку x1 или точки b в точку x2. В результате проделанных операций длина интервала [a, b] уменьшиться. Теперь к оставшится трем точкам (a, b и x1 или x2) добавим четвертую (недостающий x) по формуле a + b - <имеющийся x > и дальше все повторяем. Так продолжаем до тех пор, пока длина интервала [a, b] не станет меньше заданной точности. В этом случае за точку экстремума примем значение одного из x.
Процес поиска значения экстремума этим методом удобно проводить с занесением результатов расчетов в таблицу следующего вида
| i | a | f(a) | x1 | f(x1) | x2 | f(x2) | b | f(b) | b-a |
| 0 |
|
|
|
|
| ||||
| 1 |
| ||||||||
| … |
Подробный алгоритм поиска экстремума по этому методу приведен на рис. 7.3.
Пример 3. Найти минимум функции  методом половинного деления с точностью 0.05.
методом половинного деления с точностью 0.05.
Определение интервала поиска обосновано в примере 1. Решение примера приведем в таблце.
| i | A | f(a) | x1 | f(x1) | x2 | f(x2) | b | f(b) | b-a |
| 0 | 0,0000 | -5 | 1,9100 | -12,8119 | 3,0900 | -13,9919 | 5 | -10 | 5 |
| 1 | 1,9100 | -12,8119 | 3,0900 | -13,9919 | 3,8200 | -13,3276 | 5 | -10 | 3,09 |
| 2 | 1,9100 | -12,8119 | 2,6400 | -13,8704 | 3,0900 | -13,9919 | 3,8200 | -13,3276 | 1,91 |
| 3 | 2,6400 | -13,8704 | 3,0900 | -13,9919 | 3,3700 | -13,8631 | 3,8200 | -13,3276 | 1,18 |
| 4 | 2,6400 | -13,8704 | 2,9200 | -13,9936 | 3,0900 | -13,9919 | 3,3700 | -13,8631 | 0,73 |
| 5 | 2,6400 | -13,8704 | 2,8100 | -13,9639 | 2,9200 | -13,9936 | 3,0900 | -13,9919 | 0,45 |
| 6 | 2,8100 | -13,9639 | 2,9200 | -13,9936 | 2,9800 | -13,9996 | 3,0900 | -13,9919 | 0,28 |
| 7 | 2,9200 | -13,9936 | 2,9800 | -13,9996 | 3,0300 | -13,9991 | 3,0900 | -13,9919 | 0,17 |
| 8 | 2,9200 | -13,9936 | 2,9700 | -13,9991 | 2,9800 | -13,9996 | 3,0300 | -13,9991 | 0,11 |
| 9 | 2,9700 | -13,9991 | 2,9800 | -13,9996 | 3,0200 | -13,9996 | 3,0300 | -13,9991 | 0,06 |
| 10 | 2,9700 | -13,9991 | 2,9800 | -13,9996 | 3,0100 | -13,9999 | 3,0200 | -13,9996 | 0,05 |
| 11 | 2,9800 | -13,9996 | 2,9900 | -13,9999 | 3,0100 | -13,9999 | 3,0200 | -13,9996 | Приложение 1 - лекция, которая пользуется популярностью у тех, кто читал эту лекцию. 0,04 |
Ответ - xmin = 2.99, fmin = -13.999.
















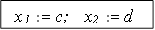









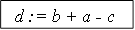








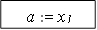



















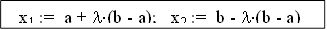







Рис. 7.3. Блок-схема алгоритма поиска экстремума функции методом
золотого сечения.






















