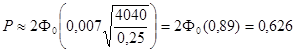Законы больших чисел и центральная предельная теорема

Лекция 7.  

 Законы больших чисел и центральная предельная теорема.

Неравенства Чебышева.

Первое неравенство Чебышева. Пусть случайная величина X³0 и существует ее математическое ожидание M(X). Тогда для любого e>0 выполнено первое неравенство Чебышева

.

Доказательство. В дискретном случае .

В непрерывном случае

.

Второе неравенство Чебышева. Пусть существуют математическое ожидание и дисперсия случайной величины . Тогда для любого  выполнено второе неравенство Чебышева

Рекомендуемые материалы

.

Доказательство проведем для непрерывного случая, для дискретного случая оно доказывается аналогично.

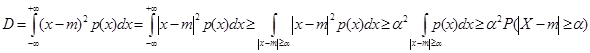
Последовательность случайных величин сходится по вероятности к числу  , если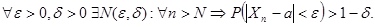

Законы больших чисел.

Законы больших чисел могут быть записаны в разных формах, но суть их состоит в том, что при большом числе случайных явлений их средний результат практически перестает быть случайным.

Теорема Чебышева

(Закон больших чисел в форме Чебышева)

При достаточно большом количестве независимых опытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности к ее математическому ожиданию.

.

Доказательство. Рассмотрим ,   .

Тогда по второму неравенству Чебышева .

Если выбрать , (- целая часть), то при n>N будет , следовательно, при n>N будет выполнено неравенство  , поэтому при тех же значениях n     будет .

Следовательно, . Теорема Чебышева доказана.

Обобщенная теорема Чебышева.

Пусть X₁,   X_n – независимые случайные величины с математическими ожиданиями m₁,…m_n и дисперсиями D₁…, D_n. Пусть дисперсии ограничены в совокупности (D_k < L, k-1,2…n). Тогда среднее арифметическое наблюденных значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий.

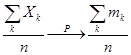
Доказательство.  Рассмотрим, как в предыдущей теореме . ,

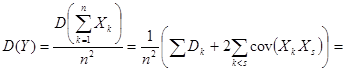
(случайные величины независимы, следовательно, и не коррелированны)

=. Отсюда по второму неравенству Чебышева следует утверждение теоремы (доказательство сходимости по вероятности проводится как в предыдущей теореме).

Теорема Маркова.

 Пусть X₁,   X_n – зависимые случайные величины с математическими ожиданиями m₁,…m_n и дисперсиями D₁…, D_n. Пусть . Тогда среднее арифметическое наблюденных значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий.

Доказательство. Доказательство сходимости по вероятности проводится как в теореме Чебышева.

Теорема Бернулли.

При неограниченном увеличении числа опытов – независимых испытаний частота события сходится по вероятности к вероятности события.

Доказательство проводится аналогично теореме Чебышева.

Предельные теоремы.

Центральная предельная теорема – это любая теорема, ставящая условия, при которых функция распределения суммы индивидуально малых случайных величин с ростом числа слагаемых сходится к нормальной функции распределения.

Центральная предельная теорема подтверждает следующее: если исход случайного эксперимента определяется большим числом случайных факторов, влияние каждого из которых пренебрежимо мало, то  такой эксперимент хорошо аппроксимируется нормальным распределением с параметрами , подобранными соответствующим образом.

Теорема Ляпунова.

Пусть X_k – независимые случайные величины, имеющие математические ожидания M(X_k) = m_k и дисперсии D(X_k) = D_k. Обозначим . Если можно подобрать такое , что , то при   равномерно по x.

Теорема Леви – Линдеберга.

Пусть X_k – независимые одинаково распределенные случайные величины, имеющие математические ожидания M(X_k) = m и дисперсии D(X_k) = . Обозначим . Тогда при   равномерно по x.

Замечание. В теореме Леви – Линдеберга (ее чаще всего и называют центральной предельной теоремой) , условие  выполнено, оно превращается в  (проверьте сами) из-за требования «одинаковости распределений», т.е. равенства вкладов случайных величин в случайную величину . Так как всегда можно выбрать , то условие выполнено.

Если рассматривать схему Бернулли, то из теоремы Леви – Линдеберга следует интегральная теорема Муавра – Лапласа.

Интегральная теорема Муавра – Лапласа.

Пусть производится n независимых испытаний, в каждом из которых с вероятностью p может появиться событие А.  Обозначим - число появлений события в k –ом испытании (). Обозначим  - общее число появлений события в n испытаниях (). Обозначим . Тогда при   равномерно по x.

Отсюда следует практическое правило вычисления

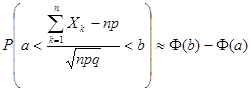
, где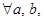

. Так как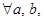то заменим  на , на , Получим формулу для вероятности нахождения числа успехов в заданном интервале:

=-.

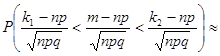
 Заменим  на , на .

Тогда .

Но .

Поэтому справедлива формула для вычисления отклонения частоты от вероятности

,

Если интервал симметричный, т.е. , то по нечетности функции Лапласа получим

Информация в лекции "Необходимое и достаточное условие существования точки перегиба графика функции" поможет Вам.

.

Пример. Вероятность появления события p = 0,8. Сделано n = 100 независимых испытаний. Найти вероятность того, что событие произойдет не менее 75 и не более 90 раз.

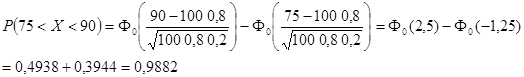
Пример. Бюффон бросил монету 4040 раз и получил герб 2048 раз. Найти вероятность отклонения частоты появления герба от вероятности.