Синтез адаптивной САУ

Лекция № 9. Синтез адаптивной САУ с эталонной моделью на основе нечеткой логики

Известно, что качество процессов управления при использовании ПИД - регуляторов существенно зависит от выбора его коэффициентов усиления 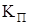,  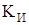и  для пропорциональной, интегральной и дифференциальной составляющей соответственно. Большинство инженеров на практике настраивают эти коэффициенты вручную, методом проб и ошибок. Эта процедура является достаточно сложной и требует опыта проектирования систем управления. С другой стороны, наличие такого опыта позволяет построить процедуру автоматической настройки коэффициентов усиления ПИД-регулятора на основе алгоритмов нечеткой логики. Ниже рассматривается один из возможных способов решения данной задачи.

Cтруктурная схема адаптивной системы управления с эталонной моделью имеет вид (рис. 3.9).

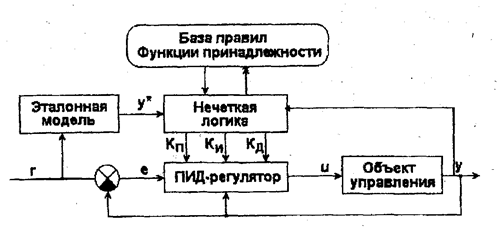
Рис. 3.9. Структурная схема нечеткой адаптивной САУ с ПИД-регулятором

Уравнение основного (ПИД-) регулятора определяется соотношением

                     (3.5)

Наличие интегральной составляющей обеспечивает нулевую статическую ошибку САУ; выбором коэффициентов 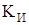, , 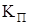и  обеспечиваются желаемые показатели качества переходных процессов. Будем учитывать 3 показателя динамики САУ:

- время  достижения 10 % от установившегося значения;

Рекомендуемые материалы

- время  нарастания, т.е. достижения 90 % от установившегося значения;

- перерегулирование .

Два из этих показателей  отмечены на рис. 3.10, где показан график переходной функции  - реакции эталонной модели на ступенчатое изменение уставки . Третий показатель  для переходного процесса, представленного на рис. 3.10, равен нулю, поскольку в качестве  выбран монотонный переходной процесс.

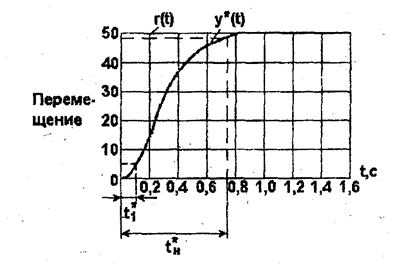
Рис. 3.10. Переходная функция эталонной модели

Будем полагать, что цель, поставленная перед нечетким регулятором, - обеспечить желаемые показатели качества системы , ,  за счет подстройки параметров основного регулятора 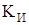, , 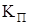и . Для этого необходимо использовать правила, основанные на опыте и интуиции. При этом учитывается следующий опыт:

1) если коэффициент усиления 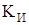 увеличивается, то время нарастания уменьшается, а перерегулирование возрастает;

2) если коэффициент усиления 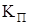 увеличивается, то время нарастания сильно уменьшается, а перерегулирование возрастает;

3) если коэффициент усиления  увеличивается, то время нарастания сохраняется, а перерегулирование слегка возрастает;

4) чтобы уменьшить время достижения 10 % от установившегося значения, необходимо уменьшить коэффициент усиления 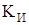 одновременно увеличить коэффициент усиления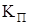

Будем рассматривать в качестве входов HP отклонения , , , а под выходами HP будем понимать настраиваемые значения коэффициентов усиления 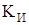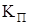, и  основного регулятора.

Базу правил HP, построенную на основе мнений экспертов, представим в виде таблицы 3.2.

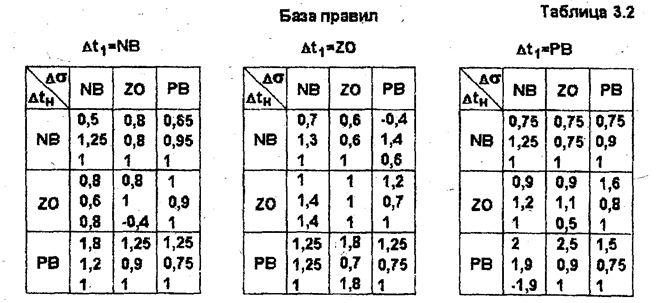
Здесь используются обозначения термов:

NB -"отрицательное большое" (negative big), ZO - "около нуля, оптимальное" (zero, optimal), PB - "большое отрицательное" (positive big).

Соответствующие этим термам функции принадлежности входных переменных HP (после нормирования диапазонов изменения указанных величин , , ) показаны на рис. 3.11.

Поясним механизм составления таблицы 3.2. В каждой из клеток этой таблицы, составленной для различных значении переменной  записаны значения поправочных коэффициентов , , , определяющих требуемый закон изменения параметров ПИД-регулятора в зависимости от значений входных лингвистических переменных HP:

; ; .     (3.6)

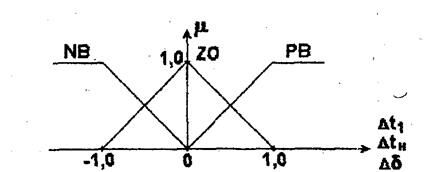
Рис. 3.11. Функции принадлежности

Примеры правил:

1°,,

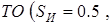
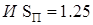
т.е. в случае затянутого, слабо демпфированного переходного процесса  необходимо на 50 % увеличить коэффициент усиления  на 25 % снизить коэффициент усиления , сохраняя неизменным значение .

2°,,

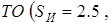
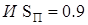
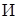
т.е. при наличии слишком форсированного переходного процесса  необходимо резко уменьшить значение , изменив даже его знак; несколько увеличить значение  сохранив на том же уровне значение , и т. д.

Таким образом, измеренные значения отклонений , ,  (входы нечеткого регулятора) после их фаззификации с помощью приведенных на рис. 3.11 функций принадлежности подвергаются обработке с использованием записанных в табл. 3.2 правил вывода.

Если на данном этапе применить метод Произведения, а для дефаззификации воспользоваться методом Центра тяжести, то получаем следующие результирующие значения поправочных коэффициентов , , :

             (3.7)

Тройная сумма в каждом из выражений (3.7) учитывает тот факт, что любое из измеренных значений , ,  принадлежит двум соседним нечетким подмножествам. Число отличных от нуля слагаемых в тройной сумме, записанной в знаменателе (3.7), равно числу активизируемых правил вывода, а величина этой суммы равна сумме уровней активности данных правил (сравните с приведенными ранее предложениями (2.22), (3.4)).

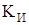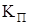После вычисления "четких" значений коэффициентов , ,  необходимо подставить их в формулы (3.6), определяющие приращения искомых параметров (, , ) ПИД-регулятора.

Пример. Объект управления описывается дискретной передаточной функцией

                                          ,                                         

11. Служебная переписка - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

где ; ; ; ; период дискретизации .

На рис. 3.12 приведены результаты моделирования системы, осуществляющей управление перемещением данного объекта.

Пунктирными линиями здесь показаны выходы управляемого объекта до выполнения процессов самонастройки указанных выше коэффициентов усиления. Сплошные линии обозначают выходы эталонной модели и совпадающие с ними выходы объекта после выполнения 5 итераций процесса самонастройки. Приведенные на рис. 3.12 результаты моделирования соответствуют случаям самонастройки для предварительно выбранной медленной (а) и быстрой (б) переходной функции САУ.

Таким образом, использование нечеткого алгоритма адаптации обеспечивает хорошее совпадение переходных процессов на выходе САУ и ее эталонной модели, сохраняя такие традиционные преимущества ПИД-регуляторов, как их низкая чувствительность к параметрическим и сигнальным возмущениям

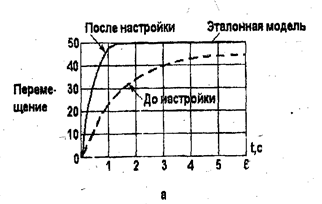
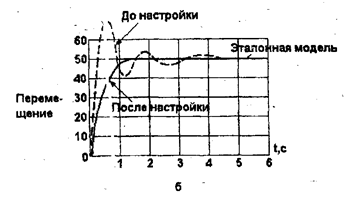
Рис. 3.12. Результаты моделирования адаптивной САУ