Интеграл Лебега. Математическое ожидание
§ 5. Интеграл Лебега. Математическое ожидание.
5.1. Пусть ( ,F,P) - конечное вероятностное пространство, т.е. существует набор множеств
,F,P) - конечное вероятностное пространство, т.е. существует набор множеств  таких, что
таких, что  при
при  и
и  , а
, а  - простая случайная величина.
- простая случайная величина.
Определение. Математическим ожиданием простой случайной величины  , обозначаемым через М
, обозначаемым через М , называется величина M
, называется величина M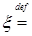
 P(Ak). Это определение корректно, так как оно не зависит от способа представления случайной величины
P(Ak). Это определение корректно, так как оно не зависит от способа представления случайной величины  . Для математического ожидания будем использовать следующее обозначение:
. Для математического ожидания будем использовать следующее обозначение:  P
P P.
P.
5.2. Дадим определение математического ожидания для случайной величины  . В силу теоремы 9 существует монотонная последовательность простых неотрицательных случайных величин
. В силу теоремы 9 существует монотонная последовательность простых неотрицательных случайных величин  таких, что
таких, что  при
при  для каждого
для каждого  . Очевидно, что M
. Очевидно, что M M
M , поэтому существует
, поэтому существует  M
M (причем он может принять значение
(причем он может принять значение  ).
).
Определение. Интеграл Лебега относительно вероятностной меры Р случайной величины  , обозначаемый М
, обозначаемый М , определяемый равенством M
, определяемый равенством M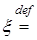
 M
M называется математическим ожиданием случайной величины
называется математическим ожиданием случайной величины  .
.
Это определение будет корректным, если значение предела не зависит от способа выбора аппроксимирующей последовательности  (иначе говоря, если
(иначе говоря, если  и
и  , то
, то  M
M =
= M
M ).
).
Лемма 13. Пусть  - простые неотрицательные случайные величины
- простые неотрицательные случайные величины  , причем
, причем  . Тогда
. Тогда  M
M ≥ M
≥ M .
.
Доказательство. Пусть  и
и  . Ясно, что
. Ясно, что  и
и  ,
,
Рекомендуемые материалы
где 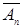
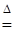
 , 1B
, 1B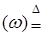
 ,
, B
B F.
F.
Поэтому
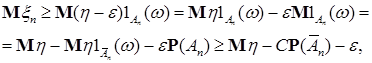
где  .
.
Следовательно  . Доказательство закончено.
. Доказательство закончено.
Замечание. Из утверждения леммы 13 следует, что 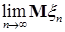
 . В силу симметрии имеем
. В силу симметрии имеем 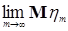
 . Отсюда вытекает корректность определения.
. Отсюда вытекает корректность определения.
5.3. Пусть теперь  - произвольная случайная величина. Обозначим
- произвольная случайная величина. Обозначим 
 .
.
Определение. Говорят, что математическое ожидание 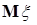 случайной величины
случайной величины  существует, если хотя бы одна из величин
существует, если хотя бы одна из величин  или
или  конечна, т.е.
конечна, т.е.  . В этом случае по определению полагается
. В этом случае по определению полагается  , а
, а 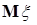 - называется интеграл Лебега от
- называется интеграл Лебега от  по мере Р.
по мере Р.
Определение. Говорят, что математическое ожидание случайной величины  конечно, если
конечно, если  и
и  . Отсюда следует, что
. Отсюда следует, что  - конечно тогда и только тогда, когда
- конечно тогда и только тогда, когда  .
.
Наряду с 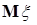 можно рассматривать и
можно рассматривать и  , если они определены, то их называют моментами
, если они определены, то их называют моментами  - порядка, где r = 1,2,…,k.
- порядка, где r = 1,2,…,k.
5.4. Свойства математического ожидания.
А) Пусть  и у случайной величины
и у случайной величины  существует
существует  , тогда существует
, тогда существует  и
и  .
.
Доказательство. Для простых функций это утверждение очевидно. Пусть  , где
, где  - простые случайные величины и
- простые случайные величины и  , следовательно
, следовательно  . Значит
. Значит 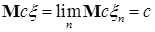
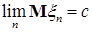
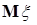 .
.
В) Пусть  , тогда
, тогда  .
.
С) Если существует  , то
, то  .
.
Доказательство. Так как  , то из А) и В) следует, что
, то из А) и В) следует, что  , то есть
, то есть  .
.
D) Если существует  , то для каждого A
, то для каждого A F существует
F существует 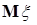
 . Если
. Если 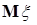 конечно, то
конечно, то 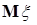
 - конечно.
- конечно.
Доказательство следует из пункта В), так как 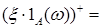
 ,
, 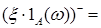
 .
.
Е) Если  и
и  - случайные величины, причем
- случайные величины, причем 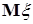
 и
и  , то
, то  .
.
Доказательство. Пусть  и
и  - последовательность простых функций таких, что
- последовательность простых функций таких, что  и
и  . Тогда
. Тогда  и
и  . Кроме того
. Кроме того  и
и  . Значит
. Значит  .
.
F) Если  , то
, то  .
.
G) Если  , Р-п.н. и
, Р-п.н. и  , то
, то  и
и  .
.
Доказательство. Пусть  , тогда
, тогда 
 , где
, где  . В силу Е)
. В силу Е)  .
.
Вместе с этой лекцией читают "4. Заключение".
Н) Пусть  и
и  , тогда
, тогда  Р - п.н.
Р - п.н.
Доказательство. Обозначим  . Очевидно, что
. Очевидно, что  .
.  поэтому в силу свойства В)
поэтому в силу свойства В)  , следовательно
, следовательно  , значит
, значит  для всех
для всех  , но
, но  .
.
I) Пусть  и
и  - случайные величины такие, что
- случайные величины такие, что  и
и  и для всех
и для всех 
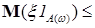
 . Тогда
. Тогда  Р - п.н..
Р - п.н..
Доказательство. Пусть  . Тогда
. Тогда 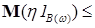
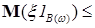
 . Поэтому
. Поэтому 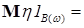
 , тогда по свойству Е)
, тогда по свойству Е)  , а в силу Н)
, а в силу Н)  P - п.н., значит Р(В)=0.
P - п.н., значит Р(В)=0.
J) Пусть  - расширенная случайная величина и
- расширенная случайная величина и  , тогда
, тогда  P - п.н..
P - п.н..
Доказательство. Действительно, пусть  и Р(А) > 0. Тогда
и Р(А) > 0. Тогда  , что противоречит предположению
, что противоречит предположению  .
.





















