Ортогональное дополнение

Ортогональное дополнение

Определение 1.16  Пусть  - подпространство евклидова пространства .

Ортогональным дополнением подпространства  называется такое множество векторов  , что .

Утверждение 1.11  Ортогональное дополнение  есть подпространство  (каково бы ни было подпространство ).

Доказательство. Из свойств скалярного умножения ясно, что для любых 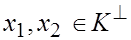 (каков бы ни был вектор ). Тем самым вместе с любыми двумя векторами ортогональное дополнение содержит их сумму. Аналогично - для умножения на число.

Утверждение 1.12  Для любых ненулевых векторов и  .

Доказательство очевидно.

Утверждение 1.13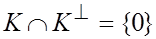 

Доказательство. Предположим, что существует ненулевой вектор . Тогда должно быть , что невозможно.

Рекомендуемые материалы

Утверждение 1.14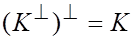 

Утверждение 1.15  .

Доказательство 1.14 и 1.15 очевидно.

Пусть теперь в подпространстве  задан ортонормированный базис . Введем также ортонормированный базис во всем пространстве : , и пусть  - обычное разложение системы по базису . Тогда, если вектор , то тогда и только тогда, когда столбец есть решение однородной системы

                                                                            (1)

(действительно, каждый столбец матрицы  есть столбец координат соответствующего вектора базиса в базисе , а при скалярном перемножении векторов , заданных разложениями в ортонормированном базисе .

Размерность пространства решений системы (1) равна . Значит,

                                      (2)

Тем самым мы доказали, что имеет место разложение произвольного конечномерного евклидова пространства  в виде объединения некоторого его подпространства и его ортогонального дополнения:

, причем

подпространства и  не имеют общих точек, кроме нулевого вектора, и выполняется соотношение размерностей (2).

Такое разложение евклидова пространства называется разложением в прямую сумму двух подпространств, каждое из которых служит ортогональным дополнением другого. Это записывают в виде:

Рекомендация для Вас - 8 Методы проектирования баз знания.

Например,

,

т.е., пространство геометрических векторов раскладывается в прямую сумму подпространства всех векторов, параллельных плоскости , и всех векторов, параллельных оси аппликат.

Более общо, если в пространстве фиксировать некоторую плоскость , то пространство геометрических векторов  раскладывается в прямую сумму:

,

где - подпространство всех векторов, параллельных плоскости , а  - подпространство всех векторов, параллельных прямой .