Дайте определение ковариационной матрицы случайного вектора. Сформулируйте и докажите основные свойства ковариационной матрицы
Дайте определение ковариационной матрицы случайного вектора. Сформулируйте и докажите основные свойства ковариационной матрицы.
Матрицей ковариаций (ковариационной матрицей) случайного вектора 
называют матрицу 
, состоящую из ковариаций случайных величин Xi и Xj.
Свойства матрицы ковариаций.
1. Матрица ковариаций является симметрической.
2. Пусть m-мерный случайный вектор 
получен из n-мерного случайного вектора 
с помощью линейного преобразования B, т. е. 
. Тогда матрица ковариаций 
случайного вектора связана с матрицей ковариаций 
случайного вектора соотношением 
.
3. Матрица ковариаций 
является неотрицательно определенной, т. е. 
для всех векторов 
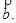
Доказательство. Утверждение 1 следует из определения матрицы ковариаций. Пусть матрица В линейного преобразования имеет вид B = (bij). Вычислим ковариацию случайных величин Yi и Yj: 
. Записывая последнее равенство в матричной форме, получаем утверждение 2. Для доказательства утверждения 3 рассмотрим скалярную случайную величину 
. В случае скалярной случайной величины Y ее дисперсия 
, и поэтому в соответствии с утверждением 2 имеем: 
, откуда в силу неотрицательности дисперсии получаем утверждение 3.
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
