Сетевое планирование в условиях неопределенности

Лекция 15

Сетевое планирование в условиях неопределенности

При определении временных параметров сетевого графика предполагалось, что время выполнения каждой работы точно известно.

Однако чаще всего продолжительность работы по сетевому графику заранее не известна и может принимать лишь одно из возможных значений. Т.е. продолжительность работы  является случайной величиной, характеризующейся своим законом распределения, а значит и своими числовыми характеристиками – средним значением или математическим ожиданием,  и дисперсией .

Практически во всех системах СПУ априори принимается, что распределение продолжительности работы обладает тремя свойствами:

- непрерывность,

- унимодальность, т.е. наличием единственного максимума у кривой распределения

- две точки пересечения кривой распределения с осью Ох.

Рекомендуемые материалы

Простейшим распределением с подобными свойствами является - распределение, которое можно использовать в качестве априорного для всех работ.

Для определения числовых характеристик и этого распределения для работы на основании опроса ответственных исполнителей проекта и экспертов определяют три временные оценки:

1) оптимистическую оценку , т.е. продолжительность работы при самых благоприятных условиях,

2) пессимистическую оценку , т.е. продолжительность работы при самых неблагоприятных условиях,

3) наиболее вероятную оценку , т.е. продолжительность работы .

Предположение о -  распределении работы  позволяет получить следующие оценки ее числовых характеристик:

                (1)

                            (2)

Следует отметить, что обычно специалистам сложно оценить наиболее вероятное время выполнения работы . Поэтому в реальных проектах используется упрощенная оценка средней продолжительности работы на основании лишь двух задаваемых временных оценок и :

                                   (3)

Зная  и , можно определить временные параметры сетевого графика  и оценивать их надежность.

При достаточно большом количестве работ, принадлежащих пути L, можно применить центральную теорему Ляпунова, на основании которой можно утверждать, что общая продолжительность пути L имеет нормальный закон распределения со средним значением , равным сумме средних значений продолжительностей составляющих его работ и дисперсией :

                                 (4)

                          (5)

Предположим, что сетевой график представляет сеть со случайными продолжительностями работ и цифры над стрелками (работами) указывают средние значения продолжительности соответствующих операций , найденные по формуле (1), и известны все дисперсии , найденные по формуле (2).

Например =61 будет означать, что длина критического пути в среднем составляет 61 сутки.

Предварительный анализ сетей со случайными продолжительностями работ, как правило , не ограничивается расчетами временных параметров сети. Важным моментом анализа становится оценка вероятности того, что срок выполнения проекта  не превзойдет заданного директивного срока T.

Полагая случайной величиной, имеющей нормальный закон распределения, получим                                        (6)

где - значение интеграла вероятностей Лапласа,

 - аргумент функции Лапласа,

- средне- квадратическое  отклонение длины критического пути.

Если  мала (например, меньше 0,3), то опасность срыва заданного срока выполнения комплекса работ велика, и необходимо принять дополнительные меры по перераспределению ресурсов по сети. Если значительна ( например более 0,8), то с достаточной степенью надежности можно прогнозировать выполнение проекта в установленный срок.

В некоторых случаях представляет интерес решение обратной задачи: определение максимального срока выполнения проекта T, который возможен с заданной надежностью ( вероятностью) . В этом случае , где - нормированное отклонение случайной величины, определяемое с помощью функции Лапласа .

Пример.

Пусть для сети известны дисперсии продолжительности работ критического пути:

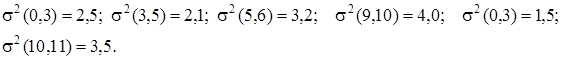
Оценить вероятность выполнения проекта в срок Т=63 сутки.

Решение

Найдем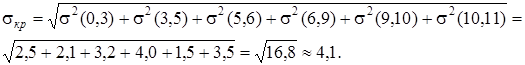

Теперь искомая вероятность

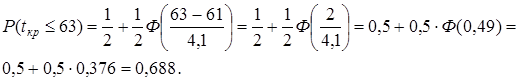
Таким образом, с известным риском, можно предполагать, что указанный проект будет выполнен в срок.

Коэффициент напряженности работы

После нахождения критического пути и резервов времени работ, оценки вероятности выполнения проекта в заданный срок, должен быть проведен всесторонний анализ сетевого графика и приняты меры по его оптимизации.

Анализ сетевого графика  начинается с анализа топологии сети, включающего контроль построения сетевого графика, установление целесообразности выбора работ.

Затем проводится классификация и группировка работ по величинам резерва времени. Следует отметить, что величина полного резерва времени не всегда может достаточно точно характеризовать, насколько напряженным является выполнение той или иной работы некритического пути. Все зависит от того, на какую последовательность работ распространяется вычисленный резерв, какова продолжительность этой последовательности.

Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициента напряженности работ.

Коэффициентом напряженности  работы называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь:

                           (7)

где - продолжительность максимального пути, проходящего через работу ;

- продолжительность (длина) критического пути;

- продолжительность отрезка рассматриваемого пути, совпадающего с критическим путем.

Данную формулу можно привести к виду:

,

где - полный резерв времени работы .

Коэффициент напряженности  может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути).

Пример

Найти коэффициент напряженности работы (1,4)  для сетевого графика.

Решение

Длина критического пути =61 сутки. Максимальный путь, проходящий через работу (1,4), это путь   - имеет продолжительность суток. Максимальный путь  совпадает с критическим путем на отрезкепродолжительностью =13+6+13=32 сутки. Используя формулу для коэффициента напряженности, найдем

.

Зная полный резерв времени работы (1,4) , по другой формуле также можно найти коэффициент напряженности работы (1,4)

В лекции "2.1 Установление диктатуры пролетариата в Югославии" также много полезной информации.

.

Чем ближе к 1 коэффициент напряженности, тем сложнее выполнить данную работу в установленные сроки. Чем ближе к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу.

Вычисленные коэффициенты напряженности работ позволяют квалифицировать работы по зонам:

- критическая зона  > 0,8,

- подкритическая зона ,

- резервная зона <0,6.