Алгоритм нахождения кратчайшего пути
Алгоритм нахождения кратчайшего пути
Неформально можно сказать, что кратчайшим путем из vi в vj, не проходящим через узлы, индексы которых больше k, будет более короткий из следующих двух путей:
· кратчайший путь, не проходящий через узлы, индексы которых больше k-1;
· кратчайший путь из vi в vk и затем в vj, не проходящий через другие узлы, индексы которых больше k-1, то есть
 |
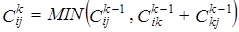Чтобы превратить алгоритм вычисления стоимости в алгоритм нахождения кратчайшего пути, зададим l(vi, vj) как стоимость ребра (vi, vj), если оно есть, и +¥ - иначе.
Теперь заменим строку 5 алгоритма последней формулой. Значение c(vi, vj), полученное с помощью алгоритма, будет наименьшей стоимостью, (то есть суммой стоимостей ребер) пути из всех путей между vi и vj.
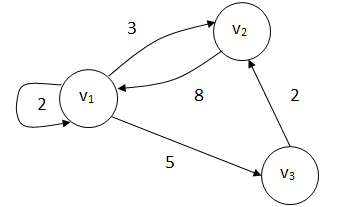
Например, рассмотрим граф G = (V, E) (рис.15).
Рекомендуемые материалы
Рис.15. Ориентированный граф
Результат работы алгоритма принято оформлять в виде совокупности таблиц, каждая из которых содержит сумму меток путей, идущих из vi в vj, но проходящих через вершины, индексы которых не больше чем k.
| l(vi, vj) | |||
| v1 | v2 | v3 | |
| v1 | 2 | 8 | 5 |
| v2 | 3 | ¥ | ¥ |
| v3 | ¥ | 2 | ¥ |
| Cij, k=0 | |||
| v1 | v2 | v3 | |
| v1 | 0 | 8 | 5 |
| v2 | 3 | 0 | ¥ |
| v3 | ¥ | 2 | 0 |
| Cij, k=1 | |||
| v1 | v2 | v3 | |
| v1 | 0 | 8 | 5 |
| v2 | 3 | 0 | 8 |
| v3 | ¥ | 2 | 0 |
| Cij, k=2 | |||
| v1 | v2 | v3 | |
| v1 | 0 | 8 | 5 |
| v2 | 3 | 0 | 8 |
| v3 | 5 | 2 | 0 |
| Cij, k=3 | |||
| v1 | v2 | v3 | |
| v1 | 0 | 7 | 5 |
| v2 | 3 | 0 | Рекомендуем посмотреть лекцию "ТУРГЕНЕВ Иван Сергеевич". 8 |
| v3 | 5 | 2 | 0 |
 |
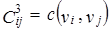![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
