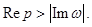Свойства изображения
§2. Свойства изображения.
1. Линейность. Пусть 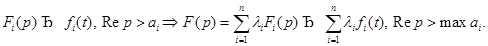
{Доказательство следует из линейных свойств интеграла}
Пример. 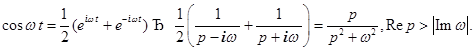
2. Пусть  тогда
тогда 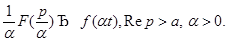
{ }
}
3. Теорема запаздывания.
Пусть  и
и  {б/д}
{б/д}
Эта теорема часто используется в случае периодических функций.
Рекомендуемые материалы
4. Изображение производной. Пусть  удовлетворяет условиям существования изображения. В этом случае
удовлетворяет условиям существования изображения. В этом случае 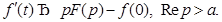
{ }
}
Пример. 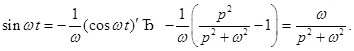
В общем случае: {доказательство аналогично}
{доказательство аналогично}
В основном, эти формулы применяют при решении дифференциальных уравнений.
5. Изображение интеграла.
Пусть  тогда
тогда  {б/д}
{б/д}
6. Изображение свертки.
Определение.  называется функция φ(t), определенная равенством:
называется функция φ(t), определенная равенством:  { замена переменных:
{ замена переменных:  }
}
Пусть  В этом случае
В этом случае  {б/д}
{б/д}
7. Дифференцирование изображения.
Пусть  тогда
тогда  {доказательство сводится к дифференцированию несобственного интеграла по параметру}
{доказательство сводится к дифференцированию несобственного интеграла по параметру}
В общем случае имеет место формула 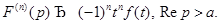
Полученные формулы часто используются для вывода изображений функций вида tn f(t).
Пример. f(t) = t sinωt. 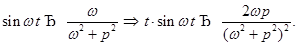
8. Интегрирование изображения. Пусть  и функция
и функция  удовлетворяет
удовлетворяет
условиям существования изображения, тогда  {б/д}
{б/д}
Пример. 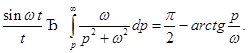
9. Теорема смещения.
Пусть 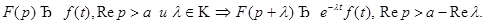
{ }
}
Пример.  (см. пример 3, §1)
(см. пример 3, §1)
СВОЙСТВА ИЗОБРАЖЕНИЙ
1)  2)
2) 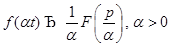
3) 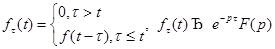
4) 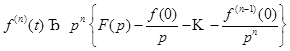
5)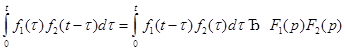
6)  7)
7) 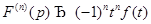
8)  9)
9) 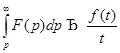
ИЗОБРАЖЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1)  2)
2) 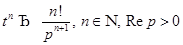
3)  4)
4) 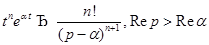
5)  6)
6)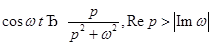
Если Вам понравилась эта лекция, то понравится и эта - 13 Функции конфликта.
7)  8)
8) 
9) 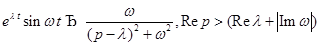
10) 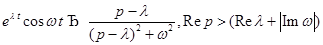
11)  , 12)
, 12)  ,
,