Приложение Ж Обобщённое обращение матрицы
П.8. Обобщённое обращение матрицы
Рассмотрим теперь обобщённые обращения тех матриц, которые не имеют обратных в обычном смысле [см. (П.5.1)]. Решение совместной системы уравнений Ax=с можно получить использованием обобщённого обращения матрицы А.
Определение и свойства
Обобщённым обращением матрицы A=Аnp является любая матрица A–, удовлетворяющая условию
AA–A=A. (П.8.1)
Обобщённое обращение не является единственным, за исключением случая, когда матрица А невырожденная. В этом случае A–=A–1. Обобщённое обращение называют также квазиобращением.
Каждая квадратная или прямоугольная матрица имеет обобщённую обратную матрицу. Это справедливо и для векторов. Например, пусть дан вектор
х= .
.
Тогда, удовлетворяющим условию (П.8.1) обобщённым обратным вектора х является x1–= [1, 0, 0, 0]. Другими обобщёнными обратными вектора х являются x2–= [0, 1/2, 0, 0], x3–= [0, 0, 1/3, 0] и x4–= [0, 0, 0, 1/4]. Для каждого вектора xi–, имеем
Рекомендуемые материалы
xxi–х=х1=х, при i =1, 2, 3, 4.
В этом пояснении; х - вектор-столбец и xi– - вектор-строка. Эта закономерность обобщена в следующей теореме.
Теорема П.8.1. Если матрица А размеров nxp, то любая её обобщённая обратная А– размеров pxn.
Доказательство: По определению АА–А=А. Если А=Аnp, то для выполнения умножения А– должна быть размеров рxn.
□
В следующем примере даются два пояснения обобщенных обращений некоторой вырожденной матрицы.
Пример П.8.1. Пусть дана матрица
А= . (П.8.2)
. (П.8.2)
Третья строка матрицы А представляет собой сумму первых двух строк и вторая строка не является кратной первой, следовательно, А имеет ранг 2. Даны две обобщенные обратные матрицы
А1–= и А2–=
и А2–= . (П.8.3)
. (П.8.3)
Легко проверить умножением, что AА1–A=A и AА2–A=A.
□
Методы получения обобщенных обратных матриц А1– и А2– в (П.8.3) представлены в теореме П.8.2 и в следующим за ней пятиступенчатом алгоритме.
Теорема П.8.2. Пусть матрица А=Аnp ранга r и она разделена на подматрицы в виде
А= ,
,
где A11 размеров rxr и ранга r. Тогда обобщённая обратная матрицы А даётся выражением
А–= ,
,
где три нулевые матрицы О таких размеров, что А– размеров pxn.
Доказательство: Умножением разделённых матриц, как дано в (П.3.1), получаем
AА–A= A=
A= .
.
Чтобы показать, что A21A11–1A12=A22, умножим А слева на матрицу
В= ,
,
где О и I соответствующих размеров, чтобы получить
ВA= .
.
Матрица В невырожденная и поэтому [по пункту 2 теоремы П.4] ранг матрицы BA получен r=ранг(A). В произведении BA подматрица  имеет ранг r и, следовательно, столбцы, начинающиеся в A12, являются линейными комбинациями столбцов, начинающихся в A11. Эта линейная зависимость столбцов подматрицы
имеет ранг r и, следовательно, столбцы, начинающиеся в A12, являются линейными комбинациями столбцов, начинающихся в A11. Эта линейная зависимость столбцов подматрицы  от столбцов подматрицы
от столбцов подматрицы  с использованием некоторой матрицы Q может быть выражена в виде
с использованием некоторой матрицы Q может быть выражена в виде
 =
= Q. (П.8.4)
Q. (П.8.4)
Выполняя умножение, как в (П.2.19), правая часть выражения (П.8.4) становится
 =
= Q=
Q= =
=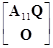
Таким образом, А22–A21A11–1A12=О откуда и получаем
А22=A21A11–1A12.
□
Следствие 1. Положим матрица А=Аnp ранга r и разделена на подматрицы, как в теореме П.8.2, где A22 размеров rxr и ранга r. Тогда обобщенная обратная матрицы А задаётся выражением
А–= , (П.8.5)
, (П.8.5)
где три нулевые матрицы О таких размеров, что А– размеров pxn.
□
Невырожденная подматрица матрицы А необязательно должна быть в положении A11 или A22, как в теореме П.8.2 или её следствии. Теорема П.8.2 может быть расширена до следующего алгоритма отыскания обобщенной обратной матрицы А– для любой матрицы А=Аnp ранга r [Searle (1982) стр.218]:
- Найти любую невырожденную подматрицу С размеров rxr. При этом необязательно чтобы элементы С занимали соседние строки и столбцы в А.
- Найти С–1 и затем (С–1)Т.
- Заменить элементы С элементами (С–1)Т.
- Заменить все другие элементы в А нулями.
- Транспонировать полученную матрицу.
- В результате получается А–.
Некоторые свойства обобщённых обращений приведены в следующей теореме.
Теорема П.8.3. Пусть матрица А=Аnp ранга r, А– - любая обобщённая обратная матрицы A и (AТA)– - любая обобщённая обратная матрицы AТA. Тогда:
- ранг(A–A)=ранг(AA–)=ранг(A)=r,
- матрица (A–)Т является обобщённой обратной матрицы AТ, то есть (AТ)–=(A–)Т,
- A=A(AТA)–AТA и AТ=AТA(AТA)–AТ,
- матрица (AТA)–AТ является обобщённой обратной для А, то есть, A–=(AТA)–AТ,
- матрица A(AТA)–AТ симметричная, имеет ранг r и является инвариантной к выбору (AТA)–, то есть, A(AТA)–AТ остается той же независимо от того какая используется обобщенная обратная (AТA)–.
Доказательство:
1. По пункту 1 теоремы П.4 ранг(A–A) ≤ ранг(A) и ранг(A) =ранг(AA–A) ≤ранг(A–A). Следовательно, ранг(A–A)=ранг(A).
2. AТ=(AA–A)Т=AТ(A–)ТAТ.
3. Пусть W=A[I–(AТA)–AТA] и найдём произведение
WТW=[I–(AТA)–AТA][AТA–AТA(AТA)–AТA]
=[I–(AТA)–AТA]О=О.
Тогда по пункту 4 теоремы П.2.3 имеем W=О и A=A(AТA)–AТA.
4. По пункту 3 получаем A[(AТA)–AТ]A=A(AТA)–AТA=A.
5. [Searle (1982) cтр.222] Покажем, что A(AТA)–AТ инвариантна к выбору (AТA)–. Пусть В обобщённая обратная матрицы AТA возможно отличная от другой её обобщённой обратной С. По пункту 3 тогда А=АВAТA и А=АСAТA, так что АВAТA=АСAТA. Это означает АВAТ=АСAТ и чтобы доказать надо показать, что (АВAТA–АСAТA)(ВТAТ–СТAТ)≡(АВAТ–АСAТ)(АВAТ–АСAТ). Левая сторона равна О, так как АВAТA=АСAТA. Тогда и правая сторона равна О и по пункту 2 теоремы П2.3 АВAТ–АСAТ=О. Чтобы показать симметрию, пусть S будет симметричной обобщённой обратной матрицы AТA. Тогда АSAТ симметричная и АВAТ=АSAТ, так как АВAТ инвариантна к (AТA)–. Отсюда АВAТ также симметричная. Чтобы показать, что ранг[A(AТA)–AТ]=r, используем пункты 1 и 4.
□
Обобщённая обратная симметричной матрицы необязательно будет симметричная. Однако верно и то, что для симметричной матрицы всегда можно найти симметричную обобщённую обратную. Здесь будем считать, что обобщённые обратные симметричных матриц симметричные.
Обобщённые обращения и системы уравнений
Обобщённые обращения могут использоваться для нахождения решения системы уравнений.
Теорема П.8.4. Если система уравнений Ах=с совместная и A– - любая обобщённая обратная матрицы А, то решением этой системы является х=A–с.
Доказательство: Так как AA–A=А, то, умножая справа на х, имеем
AA–Aх=Ах.
Заменяя в этом уравнении Ах на с, получаем
AA–с=с.
Записывая последнее в виде A(A–с)=с, видим, что A–с является решением уравнения Ах=с.
□
Различные варианты матрицы A– приводят к различным решениям системы Ах=с.
Теорема П.8.5. Если система уравнений Ах=с совместная, то все возможные её решения могут быть получены следующими двумя методами:
- По формуле х=A–с+(A–A–I)h с использованием определенной A–, при всех возможных значениях произвольного вектора h.
- Использованием всех возможных вариантов A– в х=A–с, при условии с≠0.
Доказательство: [Searle (1982) стр.238]
1. Положим вектор х является решением системы Ах=с. Выберем h=–х. Тогда х=A–с +(A–A–I)h=A–с–(A–A–I)х=A–с обращается в решение. Следовательно, соответствующим выбором h любое решение х может быть представлено в форме х. То есть все решения могут быть получены по формуле х=A–с+(A–A–I)h.
Доказательство пункта 2 теоремы основывается на следующей лемме.
Лемма. Для произвольного вектора h=hq и известного ненулевого вектора с=сp существует такая произвольная матрица Х=Хqp, что h=Хс.
Доказательство леммы: Так как с≠0, то хотябы один его элемент сk ненулевой. Запишем h=(hi) и Х=(хij) при i=1, 2, …, q и j=1, 2, …, p. Пусть хij=hi/сk для j=k и хij=0 для остальных j. Тогда Хс=h и матрица Х произвольная.
□
2. Для обобщённой обратной A– матрицы А решением системы Ах=с является A–с +(A–A–I)h с произвольным вектором h. Допуская h=–Хс для произвольной матрицы Х, как в лемме, это решение становится
A–с+(A–A–I)h=[A–AA–+(I–A–A)X+(–A–)(AA––I)]с=A*с
с матрицей А* данной в [Searle (1982) cтр.220], то есть любое решение может быть представлено в форме A*с.
□
Необходимое и достаточное условие чтобы система Ах=с была совместной, может быть сформулировано в терминах обобщенной обратной матрицы A [Graybill (1976) стр.36].
Теорема П.8.6. Система уравнений Ах=с имеет решение, если и только если для любой обобщенной обратной A– матрицы А соблюдается равенство
AA–c=c. (П.8.6)
Доказательство: Положим, что система уравнений Ах=с совместная. Тогда по теореме П.8.4 выражение х=A–с является её решением. Умножая с=Ах слева на AA–получаем
Рекомендуем посмотреть лекцию "12.3 Диагностика неисправностей манипуляторов".
AA–с=AA–Ах=Ах=с.
Обратно, пусть AA–с=с. Умножим х=A–с слева на А чтобы получать
Ах=AA–с=с.
Следовательно, решение существует в виде х=A–с.
□
Теорема П.8.6, как и теорема П.7.1, служит для выяснения, является ли система уравнений совместной.





















