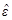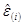Ортогональное разложение функции модели
8.3. Ортогональное разложение функции модели
Пусть в модели (8.1) с р факторами, значения которых представлены столбцами матрицы Х, вектор b параметров разделён на два подвектора b1 и b2 параметров для р1 и р2 факторов со значениями в столбцах соответственно матриц Х1 и Х2, так что функция модели Xb представляется в виде
Xb=Х1b1+Х2b2. (8.3.1)
В ней более простая часть Х1b1 может быть использована для моделирования изменений переменных отклика в эксперименте, а часть Х2b2 представляет новые члены модели, которые должны быть добавлены, если модель с функцией Х1b1 окажется неадекватной. Далее положим, что матрицы Х1 и Х2 между собой ортогональны, так что Х1ТХ2=О. Тогда формулу  =(ХТХ)–1ХТy, дающую вектор
=(ХТХ)–1ХТy, дающую вектор  оценки вектора b методом наименьших квадратов, тоже можно разделить на две части
оценки вектора b методом наименьших квадратов, тоже можно разделить на две части
 1=(Х1ТХ1)–1Х1Тy и
1=(Х1ТХ1)–1Х1Тy и  2=(Х2ТХ2)–1Х2Тy.
2=(Х2ТХ2)–1Х2Тy.
Более того, получаемая в результате регрессии сумма квадратов ( –b)ТХТХ(
–b)ТХТХ( –b) для данной выражением (8.3.1) функции модели может быть записана тоже в разделённом виде. Это получается, если вектор (b–
–b) для данной выражением (8.3.1) функции модели может быть записана тоже в разделённом виде. Это получается, если вектор (b– ) и матрицу Х представить так
) и матрицу Х представить так
(b– )Т=[(b1–
)Т=[(b1– 1), (b2–
1), (b2– 2)] и Х=[Х1, Х2].
2)] и Х=[Х1, Х2].
Тогда, так как ХТХ= [Х1, Х2]=
[Х1, Х2]= =
=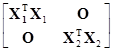 , то
, то
(b– )ТХТХ(b–
)ТХТХ(b– )=[(b1–
)=[(b1– 1), (b2–
1), (b2– 2)]
2)]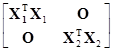
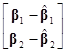
Рекомендуемые материалы
=(b1– 1)ТХ1ТХ1(b1–
1)ТХ1ТХ1(b1– 1)+(b2–
1)+(b2– 2)ТХ2ТХ2(b2–
2)ТХ2ТХ2(b2– 2)
2)
и соответствующий дисперсионный анализ модели с разделённой функцией показан в таблице 8.3.1.
Таблица 8.3.1. Дисперсионный анализ модели с разделенной на взаимно ортогональные части функцией, то есть, при Х1ТХ2=О
| Источники дисперсии | Степени свободы | Суммы квадратов |
| Регрессия только с Х1 | р1 | (b1– |
| Регрессия только с Х2 | р2 | (b2– |
| Остатки | n–р1–р2 | S( |
| Итого | n | S(b) |
В предыдущем разделе обсуждалась оценка вектора b1* параметров модели у=X1b1*+e*, когда правильной моделью является у=X1b1+X2b2+e. По теореме 8.2.1 имеем Е( )=b1+(X1ТX1)–1X1ТX2b2, так что оценка вектора b1* зависит от наличия X2 до тех пор, пока не будет соблюдаться условие X1ТX2=O. В случае, когда X1ТX2=O, получаем Е(
)=b1+(X1ТX1)–1X1ТX2b2, так что оценка вектора b1* зависит от наличия X2 до тех пор, пока не будет соблюдаться условие X1ТX2=O. В случае, когда X1ТX2=O, получаем Е( )=b1. В следующей теореме доказывается, что при X1ТX2=O результаты оценки векторов b1* и b1 не только имеют то же ожидаемое значение, но и в точности одинаковы.
)=b1. В следующей теореме доказывается, что при X1ТX2=O результаты оценки векторов b1* и b1 не только имеют то же ожидаемое значение, но и в точности одинаковы.
Теорема 8.3. Если X1ТX2=O, то результат оценки вектора b1 параметров адекватной модели у=X1b1+X2b2+e является таким же, как и результат оценки вектора b1* параметров неадекватной модели у=X1b1*+e*.
Доказательство: Вектор  =(X1ТX1)–1X1Тy является вектором оценки вектора b1* параметров методом наименьших квадратов. Для оценки вектора b1 адекватной модели разделим вектор
=(X1ТX1)–1X1Тy является вектором оценки вектора b1* параметров методом наименьших квадратов. Для оценки вектора b1 адекватной модели разделим вектор  =(XТX)–1XТy его оценки чтобы получить
=(XТX)–1XТy его оценки чтобы получить
 =
=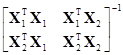
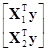 .
.
Используя обозначения в доказательстве теоремы 8.2.3, это выражение преобразуется к виду
 =
=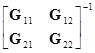
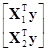
=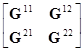
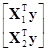 .
.
В силу (П.5.6), получаем
 =G11X1Ту+G12X2Ту
=G11X1Ту+G12X2Ту
=(G11–1+G11–1G12B–1G21G11–1)X1Ту–G11–1G12B–1X2Ту,
где B=G22–G21G11–1G12. Если G12=X1ТX2=O, то  сводится к
сводится к
 =G11–1X1Ту
=G11–1X1Ту
=(X1ТX1)–1X1Тy,
что является таким же, как для  .
.
□
Ортогонализация двух частей матрицы модели
В случае, когда подматрицы Х1 и Х2 разделённой на части матрицы Х=[Х1, Х2] модели взаимно не ортогональны, что получается, если значения факторов при планировании эксперимента выбираются произвольно, то для того чтобы матрицы Х1 и Х2 были между собой ортогональны необходимо осуществить их взаимную ортогонализацию.
Рассмотрим модель у=X1b1+e. Оценка параметров этой модели выполняется по формуле  1=(Х1ТХ1)–1Х1Тy и вектор оценки ожидаемых значений переменных отклика находится в виде
1=(Х1ТХ1)–1Х1Тy и вектор оценки ожидаемых значений переменных отклика находится в виде  =Х1
=Х1 1. Следующим из нормальных уравнений метода наименьших квадратов важным следствием оценки является то, что вектор остатков
1. Следующим из нормальных уравнений метода наименьших квадратов важным следствием оценки является то, что вектор остатков
y– =y–Х1
=y–Х1 1
1
ортогонален каждому столбцу матрицы Х1. Это даёт общий метод нахождения такого составляющего вектора уо для вектора y, который ортогонален имеющему р1 измерений векторному пространству Ст(Х1) чьими базисными векторами являются столбцы матрицы Х1. Ортогональный пространству Ст(Х1) вектор yо находится так
yо=y– =y–Х1
=y–Х1 1=(I–Р1)y,
1=(I–Р1)y,
где матрица Р1=Х1(Х1ТХ1)–1Х1Т.
Теперь, вместо вектора y рассмотрим матрицу Х2 в той же роли. В этом случае модель принимает матричный вид Х2=Х1A+E, где A - матрица параметров и E - матрица ошибок. Считая Е(E)=О, методом наименьших квадратов результат оценки матрицы A параметров модели получается по формуле А=(Х1ТХ1)–1Х1ТХ2, а результат оценки ожидаемых значений матрицы Х2 находится в виде  =Х1А. Тогда, искомая ХО составляющая матрицы Х2 ортогональная матрице Х1 находится в виде
=Х1А. Тогда, искомая ХО составляющая матрицы Х2 ортогональная матрице Х1 находится в виде
ХО=Х2– .
.
Матрица ХО содержит р2 столбцов, каждый из которых ортогонален каждому из р1 столбцов матрицы Х1 и может быть получена также по формуле
ХО=Х2–Х1А,
где А - матрица оценки параметров размеров р1хр2, полученная посредством регрессии каждого столбца матрицы Х2 во все столбцы матрицы Х1. Как было отмечено ранее, матрицу А называют также матрицей совмещения или смещения.
В случае, когда матрицы Х1 и Х2 между собой не ортогональны, модель с функцией (8.3.1) можно преобразовать следующим образом
y=Х1b1+Х1Аb2–Х1Аb2+Х2b2+ε
=Х1(b1+Аb2)+(Х2–Х1А)b2+ε
=Х1b+ХОb2+ε,
где b=b1+Аb2. Здесь матрицы Х1 и ХО между собой ортогональны. Соответствующий дисперсионный анализ модели с ортогональными между собой частями её матрицы показан в таблице 8.3.2.
Таблица 8.3.2. Дисперсионный анализ модели с ортогональными между собой частями её матрицы
| Источники дисперсии | Степени свободы | Суммы квадратов |
| Регрессия только с Х1 | р1 | (b– |
| Дополнительно для Х2 | р2 | (b2– |
| Остатки | n–р1–р2 | S( |
| Итого | n | S(b) |
В результате ортогонализации между собой частей матрицы модели должны быть отмечены следующие пункты:
1. Полученный для модели y=Х1b+ХОb2+ε вектор  оценки такой же, как и для модели y=Х1b+ε1, которая содержит только матрицу Х1.
оценки такой же, как и для модели y=Х1b+ε1, которая содержит только матрицу Х1.
2. Если модель y=Х1b+ε1 неадекватна и необходимо включить в неё дополнительные факторы, то вектор  2 оценки дополнительных параметров будет тем же, что получается методом наименьших квадратов для модели с функцией Xb=Х1b1+Х2b2 и ортогональными между собой матрицами Х1 и Х2, или для модели y=ХОb2+ε2.
2 оценки дополнительных параметров будет тем же, что получается методом наименьших квадратов для модели с функцией Xb=Х1b1+Х2b2 и ортогональными между собой матрицами Х1 и Х2, или для модели y=ХОb2+ε2.
(Выполнение пунктов 1 и 2 обеспечивается тем, что матрицы Х1 и ХО ортогональны между собой, то есть Х1ТХО=О, но сами по себе они могут быть не ортогональными.)
3. Если необходимы дополнительные факторы для превращения неадекватной модели y=Х1b1+ε в адекватную, где b2≠0, то вектор  будет результатом смещённой оценки вектора b1, а вернее результатом оценки совмещения b1+Аb2.
будет результатом смещённой оценки вектора b1, а вернее результатом оценки совмещения b1+Аb2.
4. Необходимость присутствия части Х2b2 в функции модели будет показана величиной суммы квадратов “Дополнительной для Х2” с р2 степенями свободы, когда в этой сумме квадратов вектор b2=0.
5. “Дополнительная для Х2” сумма квадратов может быть получена посредством использования сначала более простой модели y=Х1b1+ε, а затем более разработанной модели y=Х1b1+Х2b2+ε и вычислением разности сумм квадратов остатков для этих моделей.
Ортогонализация столбцов матрицы модели
Кроме взаимной ортогонализации двух частей матрицы модели, состоящих из нескольких столбцов, можно сделать ортогональными между собой все столбцы этой матрицы. Есть процедура последовательного преобразования столбцов матрицы модели, так что каждый новый преобразованный столбец ортогонален ранее преобразованным столбцам [Draper, Smith (1998) стр.383]. Преобразование столбцов осуществляется по формуле
xjо=(I–X(XTX)–1XT)xj (8.3.2)
где X - матрица уже преобразованных столбцов, xj - следующий подлежащий преобразованию вектор-столбец матрицы и хjо - преобразованный вектор-столбец ортогональный всем столбцам матрицы Х. В этой процедуре вектор хjо в действительности является вектором остатков для вектора xj после того как он был спроецирован в пространство вектор-столбцов матрицы Х.
Исходной матрицей этого преобразования может быть матрица, состоящая из столбца 1 значений фактора х0 и столбца нормированных значений фактора х1, так как само нормирование делает его ортогональным столбцу 1. Если существует линейная зависимость между столбцами формируемой матрицы Х и вновь присоединяемым столбцом, то этот столбец получается состоящим из очень малых чисел или возможно нулей. Такой столбец присоединять нет смысла, так как фактор с нулевыми или почти нулевыми значениями оказывает приблизительно нулевое воздействие на переменную отклика. Добавление такого столбца приводит к линейной или почти линейной зависимости столбцов матрицы Х. Это, в свою очередь, приводит к вырожденной или плохо обусловленной матрице ХТХ и её обратную (ХТХ)–1 нельзя получить.
Пример 8.3. Выполним нормирование рассматриваемых в примере 7.1 факторов по формуле x=(ξ– )/S, где
)/S, где  =
= и S=
и S= . Тогда данные таблицы 7.1 с нормированными значениями факторов получаются, как показано в таблице 8.3.3.
. Тогда данные таблицы 7.1 с нормированными значениями факторов получаются, как показано в таблице 8.3.3.
В результате такого нормирования факторов x1 и x2 получены нормированные их значения. Векторы нормированных значений этих факторов можно считать ортогональными вектору 1 матрицы модели, так как 1Тx1=1,477х10–14 и 1Тx2=3,889х10–14. Однако эти векторы не ортогональны между собой, так как x1Тx2=1,22. Чтобы сделать их ортогональными воспользуемся формулой (8.3.2). В этой формуле матрица Х=[1, x1], а преобразуемым вектором является x2. Полученные в результате преобразования значения элементов преобразованного вектора х2о показаны в таблице 8.3.3. Этот вектор ортогонален векторам 1 и x1, так как 1Тx2о=0 и x1Тx2о=0. Заметим, что если необходима строгая ортогональность столбцов матрицы модели, то начинать надо с ортогонализации векторов 1 и x1. При этом исходной матрицей будет Х=1.
Таблица 8.3.3. Значения нормированных факторов, коэффициента (у) усиления и оценок их ожидаемых значений, остатков и других данных анализа
| Опыт | x1 | x2 | х2о | у |
|
| ri | hii |
| di |
| 1 | –1,849 | –1,325 | –1,163 | 1004 | 1003 | 1,3 | 0,013 | 0,413 | 2,369 | 3,7x10-5 |
| 2 | 0,597 | –1,325 | –1,377 | 1636 | 1425 | 211 | 1,669 | 0,233 | 275,762 | 0,282 |
| 3 | –1,849 | 1,033 | 1,194 | 852 | 874,6 | –22,6 | –0,205 | 0,418 | –38,806 | 0,010 |
| 4 | 0,597 | 1,033 | 0,981 | 1506 | 1297 | 209 | 1,585 | 0,166 | 251,195 | 0,167 |
| 5 | 0,597 | –0,539 | –0,591 | 1272 | 1382 | –110 | –0,81 | 0,122 | –125,153 | 0,030 |
| 6 | 0,597 | –0,932 | –0,984 | 1270 | 1403 | –133 | –1,008 | 0,167 | –159,84 | 0,068 |
| 7 | 0,597 | 1,033 | 0,981 | 1269 | 1297 | –27,5 | –0,208 | 0,166 | –33,012 | 0,003 |
| 8 | –1,849 | –0,146 | 0,015 | 903 | 938,6 | –35,6 | –0,297 | 0,316 | –52,012 | 0,014 |
| 9 | 0,597 | –0,146 | –0,198 | 1555 | 1361 | 194 | 1,416 | 0,100 | 215,99 | 0,074 |
| 10 | 0,597 | –1,325 | –1,377 | 1260 | 1425 | –165 | –1,299 | 0,233 | –214,625 | 0,171 |
| 11 | 0,597 | 1,426 | 1,374 | 1146 | 1275 | –129 | –1,019 | 0,233 | –168,362 | 0,105 |
| 12 | 0,597 | –0,146 | –0,198 | 1276 | 1361 | –84,5 | –0,616 | 0,100 | –93,908 | 0,014 |
| 13 | 0,597 | 1,504 | 1,452 | 1225 | 1271 | –45,9 | –0,366 | 0,249 | –61,119 | 0,015 |
| 14 | –0,422 | –0,146 | –0,109 | 1321 | 1185 | 136 | 0,984 | 0,085 | 148,931 | 0,030 |
Для модели с не ортогональными между собой векторами нормированных факторов результаты оценки ожидаемых значений коэффициента усиления находятся по формуле
 =1250+172,5х1–54,3х2,
=1250+172,5х1–54,3х2,
а для модели с ортогональными между собой векторами нормированных факторов - по формуле
 =1250+167,8х1–54,3х2,
=1250+167,8х1–54,3х2,
что подтверждает результаты, полученные в разделе 6.2 в процессе ортогонализации столбцов матрицы модели и в разделе 8.3 в процессе ортогонализации двух частей матрицы модели.
□
Оценка переменных отклика при ортогонализации матрицы модели
В разделе 7.5 показано, что при нормировании факторов модели вектор оценки ожидаемых значений переменных отклика остаётся тем же, что и для модели с ненормированными факторами. Покажем, что это справедливо и при ортогонализации столбцов матрицы модели у=Хb+e.
Начиная со столбца x1 ортогональное преобразование столбцов матрицы Х=[1, x1, x2, …, xp–1] выполняется по формулам
u1= [I–1(1T1)–11T]x1
u2= [I–X1(X1TX1)–1X1T]x2, где X1= [1, u1]
u3= [I–X2(X2TX2)–1X2T]x3, где X2= [1, u1, u2]
…
up–1= [I–Xp–2(Xp–2TXp–2)–1Xp–2T]xp–1, где Xp–2=[1, u1, u2,..., up–2]
Следовательно, матрица U модели с взаимно ортогональными столбцами имеет вид
U=[1, u1, u2, …, up–1]
={1, [I–1(1T1)–11T]x1, [I–X1(X1TX1)–1X1T]x2, …, [I–Xp–2(Xp–2TXp–2)–1Xp–2T]xp–1}
Она получается в результате произведения разделённой по столбцам матрицы Х=[1, x1, x2, …, xp–1] на диагональную матрицу
D=диаг{I, [I–1(1T1)–11T], [I–X1(X1TX1)–1X1T],..., [I–Xp–2(Xp–2TXp–2)–1Xp–2T]}.
Вектор оценки параметров модели, имеющей матрицу U, находится по формуле  =(UТU)–1UТy. Подставляя в эту формулу ХD вместо U получаем
=(UТU)–1UТy. Подставляя в эту формулу ХD вместо U получаем
 =[(ХD)Т(ХD)]–1(ХD)Тy
=[(ХD)Т(ХD)]–1(ХD)Тy
=(ХD)–1[(ХD)Т]–1(ХD)Тy
=D–1Х–1(DТХТ)–1(ХD)Тy
=D–1Х–1(ХТ)–1(DТ)–1DТХТy [в силу (П.5.5)]
=D–1(ХТХ)–1ХТy
В лекции "16 Теоремы запаздывания и свертки" также много полезной информации.
=D–1 ,
,
где  - вектор оценки параметров, вычисляемый по формуле (8.1.4).
- вектор оценки параметров, вычисляемый по формуле (8.1.4).
Преобразование i-й строки матрицы X в i-ю строку матрицы U выполняется по формуле uiс=xiсD, а преобразование uiс в xiс в виде uiсD–1=xiс. Следовательно, результат  оценки ожидаемого значения i-й переменной отклика находится так
оценки ожидаемого значения i-й переменной отклика находится так
 =uiс
=uiс =uiсD–1
=uiсD–1
=xiс .
.
Таким образом, преобразование матрицы модели путём ортогонализации её столбцов является полного ранга линейным преобразованием и по следствию теоремы 7.5 оставляет без изменения результаты оценки ожидаемых значений переменных отклика.