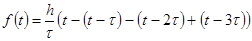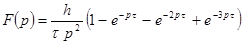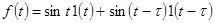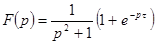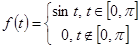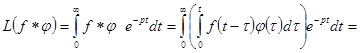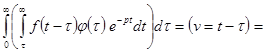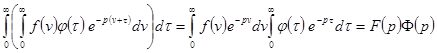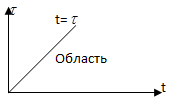Теоремы запаздывания и свертки
Лекция 2.
Теоремы запаздывания и свертки.
Теорема запаздывания. 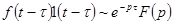
| Здесь |
|
Доказательство . Заметим, что  =0 при
=0 при  ,
,  .
.
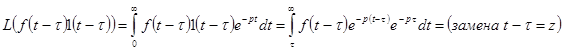
Рекомендуемые материалы
 .
.
Изображение периодической функции.
Пусть функция  - периодическая с периодом Т. Обозначим
- периодическая с периодом Т. Обозначим  .
.
Вычислим  =
= . Представим функцию
. Представим функцию  в виде
в виде
 и применим теорему запаздывания
и применим теорему запаздывания  .
.
Примеры.
1) Найти оригинал по изображению  .
.
 . По теореме запаздывания
. По теореме запаздывания  .
.
2) Найти изображение периодической функции с периодом Т. 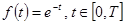
 ,
, 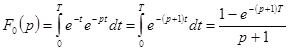
Изображения элементарных импульсов.
| Прямоугольный импульс.
|
|
|
|
|
|
|
|
| Синусоидальный импульс
|
|
Свертка.
Сверткой  двух функций называется интеграл
двух функций называется интеграл  =
= .
.
Свойства свертки.
1. Коммутативность. 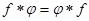
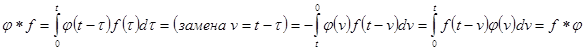
2. Ассоциативность.
 (доказательство громоздко, см. его в учебнике т.Х1).
(доказательство громоздко, см. его в учебнике т.Х1).
3.  - оригинал, если
- оригинал, если  - оригиналы.
- оригиналы.
Самостоятельно проверьте первые два требования к оригиналу. Проверим третье требование.
Пусть  . Обозначим
. Обозначим  .
.
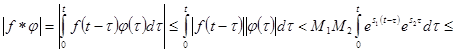
а) 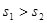
 <
< 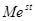
б)  .
.
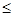
 .
.
Теорема о свертке (теорема о произведении изображений).  .
.
Доказательство.
|
= = |
|
Пример. Найти оригинал, соответствующий изображению 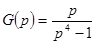
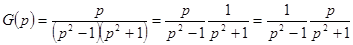

 .
.
Интеграл Дюамеля.
 ,
, 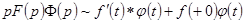
 ,
, 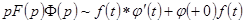
Эти соотношения называются интегралом Дюамеля.
Обратите внимание на лекцию "4. Производственное освещение".
Доказательство. Выражения, стоящие в одной строке равны по коммутативности свертки. Докажем первые соотношения в строках.
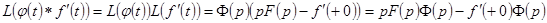
Но  . Отсюда следует справедливость первого соотношения в первой строке.
. Отсюда следует справедливость первого соотношения в первой строке.
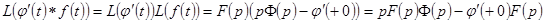
Но  . Отсюда следует справедливость второго соотношения во второй строке.
. Отсюда следует справедливость второго соотношения во второй строке.



 - «запаздывающая функция».
- «запаздывающая функция».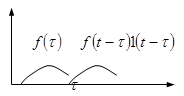
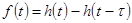
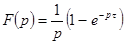
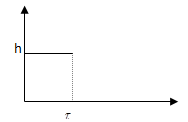
 Треугольный импульс.
Треугольный импульс.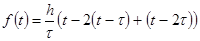
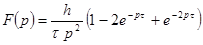
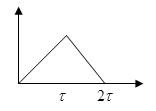
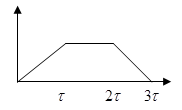
 Трапецеидальный импульс
Трапецеидальный импульс