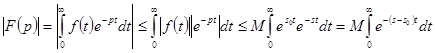Преобразование Лапласа, таблица изображений
Часть 3. Операционное исчисление
Лекция 1
Преобразование Лапласа, таблица изображений.
Преобразование Лапласа – это интегральное преобразование, при котором функция  действительной переменной
действительной переменной  преобразуется в функцию
преобразуется в функцию комплексной переменной
комплексной переменной  по формуле
по формуле  =
= .
.
Функция  называется прообразом или оригиналом, функция
называется прообразом или оригиналом, функция называется образом или изображением (по Лапласу). Принято обозначать соответствие оригинала и изображения
называется образом или изображением (по Лапласу). Принято обозначать соответствие оригинала и изображения  .
.
Не всякая функция  может быть оригиналом, она должна удовлетворять определенным требованиям.
может быть оригиналом, она должна удовлетворять определенным требованиям.
Рекомендуемые материалы
Требования, предъявляемые к оригиналу.
1. Условия Дирихле.
q На любом конечном интервале изменения аргумента функция  может иметь не более конечного числа точек разрыва и не более конечного числа точек экстремума.
может иметь не более конечного числа точек разрыва и не более конечного числа точек экстремума.
q Допустимы только разрывы первого рода, разрывы второго рода не допускаются.
2. Условие физической реализуемости.  .
.
3. Функция  не может расти быстрее экспоненты.
не может расти быстрее экспоненты.  .
.
В операционном исчислении для обеспечения физической реализуемости любая функция умножается на функцию Хевисайда  - «единичный скачок» или единичную функцию. Это подразумевается, то есть всегда
- «единичный скачок» или единичную функцию. Это подразумевается, то есть всегда  .
.
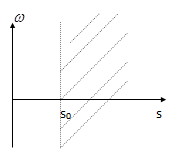
Теорема. Изображение определено в полуплоскости  и является в этой полуплоскости аналитической функцией.
и является в этой полуплоскости аналитической функцией.
| Доказательство. (Аналитичность – без доказательства) Вычислим = Из 3 требования к оригиналу Оценим |
|
=  .
.
Следствие. Если  - изображение, то
- изображение, то 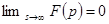
Доказательство.  .
.
Найдем изображения по Лапласу единичной функции и экспоненты.
 .
.  .
.
 .
. 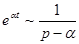
Свойства преобразования Лапласа  (простейшие теоремы).
(простейшие теоремы).
Линейность  (здесь
(здесь  ,
,  ). Докажите самостоятельно, опираясь на свойство линейности интеграла.
). Докажите самостоятельно, опираясь на свойство линейности интеграла.
Следствие.  .
.
Пример. Найдем изображения по Лапласу тригонометрических и гиперболических синуса и косинуса.
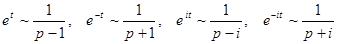
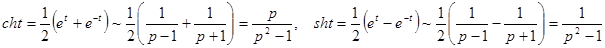
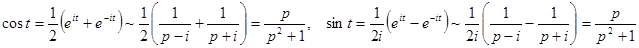
Теорема подобия.  .
.
Доказательство.  .
.
Примеры.  ,
,
 .
.
Теорема смещения.  .
.
Доказательство. 
Здесь  по теореме об области определения изображения.
по теореме об области определения изображения.
Примеры. 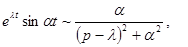
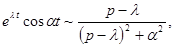
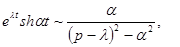
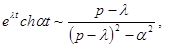
Заданы изображения найти оригиналы  .
.
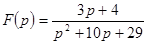

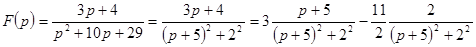
 .
.
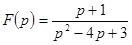
 .
.
Теоремы о дифференцировании и интегрировании.
Теорема о дифференцировании оригинала.
Пусть 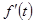 - оригинал. Тогда
- оригинал. Тогда 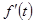
 .
.
Доказательство. 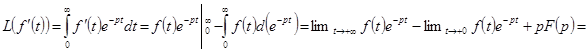
 , так как
, так как  .
.
Следствие. Если 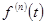 - оригинал, то
- оригинал, то 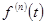
 .
.
Доказательство. 
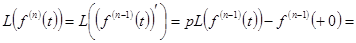
 …
… .
.
Например, 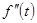
 .
.
Теоремы о начальном и конечном значениях.
Теорема о конечном значении.  .
.
Доказательство.  (теорема о дифференцировании оригинала). Перейдем к пределу при
(теорема о дифференцировании оригинала). Перейдем к пределу при  .
.
Предел левой части  ,
,
Предел правой части  . Приравнивая эти выражения, получим
. Приравнивая эти выражения, получим  .
.
Теорема о начальном значении.  .
.
Доказательство.  (теорема о дифференцировании оригинала).
(теорема о дифференцировании оригинала). 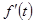 - оригинал, поэтому
- оригинал, поэтому  . Поэтому
. Поэтому  .
.
Теорема об интегрировании оригинала.  .
.
Доказательство. Обозначим  . Это – оригинал (проверьте требования к оригиналу).
. Это – оригинал (проверьте требования к оригиналу).  . Обозначим
. Обозначим 
 . По теореме о дифференцировании оригинала
. По теореме о дифференцировании оригинала  . Так как
. Так как  , то
, то  .
.
Следовательно,  .
.
Пример.  .
.
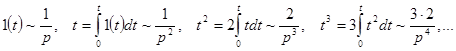
 .
.
Теорема о дифференцировании изображения.  .
.
Доказательство.  . Дифференцируем обе части по
. Дифференцируем обе части по  .
.
 . Тогда
. Тогда  .
.
Пример. Найти оригинал для изображения  .
.
 . Поэтому
. Поэтому 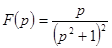
 .
.
Пример. Найти изображение функции 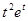 двумя способами.
двумя способами.
Вместе с этой лекцией читают "Новая глава Русь между Востоком и Западом".
1)  . По теореме смещения
. По теореме смещения 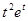
 .
.
2)  . Дважды применим теорему о дифференцировании изображения:
. Дважды применим теорему о дифференцировании изображения:  ,
,  .
.
Теорема об интегрировании изображения. Если  - оригинал, то
- оригинал, то  .
.
Доказательство. Обозначим  . Тогда
. Тогда  .
.
По теореме о дифференцировании изображения  . Но
. Но  . Поэтому
. Поэтому  =
=  , так как
, так как  .
.
Пример.  .
.



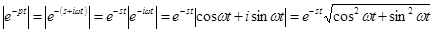
 .
. .
.