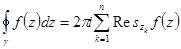Вычеты и их применение

Лекция 9.

Вычеты и их применение.

Вычетом функции f(z) в точке z₀  называется коэффициент  при z^-1 в разложении функции в ряд Лорана в окрестности этой точки.

Эквивалентное определение: вычетом функции f(z) в точке z₀  называется . В самом деле, коэффициент ряда Лорана равен . Поэтому .

Вычисление вычетов в точке  конечной плоскости.

Для различных типов особых точек (правильная, полюс, существенно особая) различны алгоритмы вычисления вычетов функции в этих точках.

Если z₀ – правильная особая точка, то ряд Лорана превращается в ряд Тейлора, в котором нет отрицательных степеней , поэтому  =0.

Если z₀ – полюс первого порядка, то разложение в ряд Лорана в окрестности этой точки  не содержит степеней , ниже, чем –1 и содержит степень -1. Разложение выглядит так.

Рекомендуемые материалы

 . Умножим обе части на .

 Перейдем к пределу при , чтобы обратились в нуль все слагаемые в правой части, содержащие целые степени .

- формула для вычета функции в полюсе первого порядка.

В том случае, когда z₀ – полюс первого порядка функции вида

, можно получить удобную в вычислениях формулу для вычета.

= - формула для вычета функции в полюсе первого порядка. Здесь использованы условия      .

Пример. Найти вычеты функции  во всех особых точках конечной плоскости.

У функции два полюса первого порядка  .

По первой формуле

                                              

  .   

Применим вторую формулу

 . , .

В том случае, когда z₀ – полюс n-го порядка, то разложение в ряд Лорана в окрестности этой точки  не содержит степеней , ниже, чем –n и содержит степень –n . Разложение выглядит так.

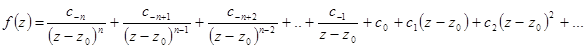
Умножим обе части на .

.

Уничтожим степень при коэффициенте дифференцированием, его надо провести  раз. Получим

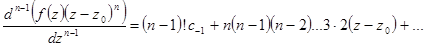
Перейдем к пределу при . Все слагаемые в правой части, содержащие целые степени  (второе, третье, четвертое и т.д.) обратятся в нуль. Отсюда имеем формулу для вычета функции в полюсе n – ого порядка:

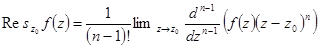
Пример. .  - полюс 1 порядка, z = 1 – полюс 2 порядка.

.

В том случае, когда точка - существенно особая точка, вычет в ней вычисляется единственным способом – непосредственным разложением функции в ряд Лорана и вычислением коэффициента при –1 степени.

Пример.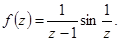  

Здесь  - существенно особая точка. Разложение в ряд Лорана в окрестности :

.

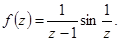
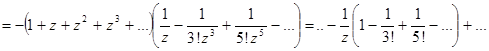
Вычетом функции в бесконечно удаленной точке  называется коэффициент , (взятый со знаком минус коэффициент при –1 ой степени в разложении в ряд Лорана в окрестности бесконечно удаленной точки).

Общая теорема о вычетах.

Доказательство. По интегральной теореме Коши для многосвязной области . Вычислим интеграл . Разложим функцию  в ряд Лорана в окрестности точки и подставим в интеграл. По равномерной сходимости степенного ряда внутри круга сходимости, проведем почленное интегрирование и используем полученный ранее результат =.

=.

Тогда =.

Теорема. Сумма вычетов функции по всей расширенной плоскости равна нулю.

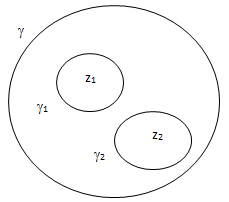
Доказательство. Выберем контур так, чтобы все особые точки функции лежали внутри контура. Тогда при обходе контура в положительном направлении надо учитывать

особые точки, попавшие внутрь контура, т.е. все особые точки конечной плоскости. По общей теореме о вычетах 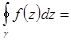. С другой стороны, при обходе контура в отрицательном направлении мы должны учитывать только бесконечно удаленную точку и интеграл получится тем же, но со знаком «минус» (свойство интеграла). Поэтому -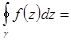. Складывая эти интегралы, получим

.

Следствие. Сумма вычетов функции по всей конечной плоскости равна вычету функции в бесконечно удаленной точке, взятому со знаком «минус».

Доказательство. По предыдущей теореме . Отсюда .

Пример. Вычислить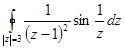

Подынтегральная функция имеет полюс второго порядка  и существенно особую точку . Вычислим вычеты в этих особых точках.

.

Разложим подынтегральную функцию в ряд Лорана в окрестности .

  

    

 =     =

 

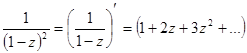
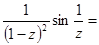
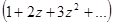
Следовательно . .

=.

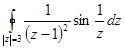Применение вычетов для вычисления несобственных интегралов.

Теорема. Пусть функция  - аналитическая в верхней полуплоскости () за исключением конечного числа особых точек , лежащих в верхней полуплоскости непрерывна  на действительной оси, удовлетворяет (при больших |z|) неравенству . Тогда  

Доказательство. Выберем контур полуокружностью радиуса , лежащей в верхней полуплоскости, с основанием – отрезком  действительной оси,  - достаточно велико, чтобы все особые точки лежали внутри контура. По общей теореме Коши о вычетах =

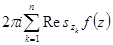
. Оценим . Поэтому . Устремляя , имеем .

Пример. Вычислить .  Подынтегральная функция, рассматриваемая как функция комплексной переменной, имеет в верхней полуплоскости имеет полюс второго порядка .

=

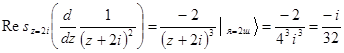
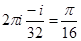
Лемма Жордана. Пусть функция  - аналитическая в полуплоскости () за исключением конечного числа особых точек. Пусть  где . Тогда  выполнено

.

Замечание. Применяя лемму Жордана к функции , можно сформулировать лемму Жордана для полуплоскости .

В лекции "5.2 Функции культурных норм" также много полезной информации.

Пусть функция  - аналитическая в полуплоскости () за исключением конечного числа особых точек. Пусть  где . Тогда  выполнено

.

Пример (стр. 214 задачника А.В. Ефимова, Б.П. Демидовича, ч.2 1986).

Вычислить интегралы , . Эти интегралы являются мнимой и действительной частями интеграла , к которому применима лемма Жордана. Подынтегральная функция, как функция комплексной переменной, имеет в в верхней полуплоскости один полюс . Вычисляя вычет и применяя общую теорему о вычетах, получим

==  +i .

Поэтому =, = .