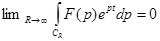Теоремы разложения
Лекция 3.
Теоремы разложения.
Сформулируем достаточные условия изображения – требования, предъявляемые к функции комплексной переменной, чтобы она была изображением некоторого оригинала.
1. Функция  - аналитическая при
- аналитическая при  (константа
(константа  определяет третье требование к оригиналу).
определяет третье требование к оригиналу).
2.  сходится (
сходится ( ).
).
3.  .
.
При выполнении этих требований функция  является изображением некоторого оригинала.
является изображением некоторого оригинала.
Теорема обращения. Пусть функция  удовлетворяет достаточным условиям изображения. Тогда справедлива формула обращения
удовлетворяет достаточным условиям изображения. Тогда справедлива формула обращения
Рекомендуемые материалы
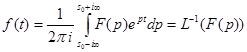
Интеграл, стоящий в правой части этой формулы, называется интегралом Римана – Меллина, он осуществляет обратное преобразование Лапласа (переход от изображения к оригиналу).
Доказательство см.т.Х1 учебника, стр.160 – 166.
Приведем без доказательства лемму Жордана (здесь она используется в доказательстве теоремы обращения и в доказательстве общей теоремы разложения, несколько иная ее форма применена в лекции 9 по ТФКП для вычисления несобственных интегралов).
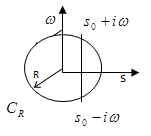
| Построим контур Лемма Жордана. Пусть Тогда
|
|
Общая (третья) теорема разложения.
Пусть  - аналитическая за исключением конечного числа особых точек
- аналитическая за исключением конечного числа особых точек 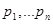
 . Пусть
. Пусть  при
при  ,
,  равномерно по аргументу
равномерно по аргументу  . Тогда
. Тогда  .
.
Доказательство. Пусть в область, ограниченную  и отрезком, соединяющим точки
и отрезком, соединяющим точки  , попало m из n особых точек. По общей теореме о вычетах
, попало m из n особых точек. По общей теореме о вычетах
 . Устремим
. Устремим  . Внутрь рассматриваемой области войдут тогда все n особых точек. К первому слагаемому может быть применена лемма Жордана, его предел при
. Внутрь рассматриваемой области войдут тогда все n особых точек. К первому слагаемому может быть применена лемма Жордана, его предел при  .будет равен нулю. Ко второму слагаемому может быть применена теорема обращения. Его предел при
.будет равен нулю. Ко второму слагаемому может быть применена теорема обращения. Его предел при  .будет равен
.будет равен  . Следовательно, в результате предельного перехода получим, сокращая обе части на
. Следовательно, в результате предельного перехода получим, сокращая обе части на  ,
,  .
.
Следствие. Первая теорема разложения.
Пусть  . Тогда
. Тогда  .
.
Доказательство. Отыщем оригинал  от изображения
от изображения  . По общей теореме разложения
. По общей теореме разложения  =
= .
.
Информация в лекции "ШАЛЯПИН Федор Иванович" поможет Вам.
По равномерной сходимости ряда Лорана допустимо его почленное интегрирование ( при вычислении вычета) и почленный переход к пределу. По общей теореме разложения
 .
.
Следствие. Вторая теорема разложения.
Пусть  имеет в качестве особых точек только полюсы
имеет в качестве особых точек только полюсы  кратности
кратности  . Тогда
. Тогда 
Доказательство теоремы сводится к применению общей теоремы разложения и формулы вычисления вычета в полюсе  порядка.
порядка.



 , отметим на ней точки с абсциссой
, отметим на ней точки с абсциссой  )
)