Решение дифференциальных уравнений и систем методом операционного исчисления
Лекция 4.
Решение дифференциальных уравнений и систем
Методом операционного исчисления.
При решении дифференциальных уравнений и систем используется теорема о дифференцировании оригинала и ее следствие – теорема об изображении n-ой производной.
Метод решения основан на том, что преобразование Лапласа сводит дифференцирование в пространстве оригиналов к умножению на p в пространстве изображений. Поэтому дифференциальное уравнение с постоянными коэффициентами с пространстве оригиналов переходит в алгебраическое уравнение в пространстве изображений. При этом учитываются и начальные условия, что удобно при решении задачи Коши.
Получив решение алгебраического уравнения в пространстве изображений, мы получаем решение в виде некоторого изображения – функции от p. Остается найти соответствующий ему оригинал по свойствам преобразования Лапласа (теоремам подобия, смещения, запаздывания, дифференцирования и интегрирования) или теоремам разложения.
Пусть задано дифференциальное уравнение с постоянными коэффициентами  относительно неизвестной функции
относительно неизвестной функции  и ее производных с правой частью – функцией
и ее производных с правой частью – функцией  , являющейся оригиналом
, являющейся оригиналом
 .
.
Рекомендуемые материалы
Требуется решить задачу Коши для этого уравнения при начальных условиях  .
.
Применим преобразование Лапласа к обеим частям равенства.

 .
.
Приведем коэффициенты при  в левой части и перенесем члены, зависящие от начальных условий, в правую часть.
в левой части и перенесем члены, зависящие от начальных условий, в правую часть.
 ,
,
где  - характеристический многочлен,
- характеристический многочлен,
 Найдем изображение решения
Найдем изображение решения
 .
.
Здесь первое слагаемое дает вклад правой части в решение, второе слагаемое – вклад начальных условий. Если начальные условия нулевые, то  и второе слагаемое пропадает.
и второе слагаемое пропадает.
Примеры.
1. 
 ,
, 
Первые два слагаемых соответствуют  , оригинал для третьего слагаемого находим по теореме об интегрировании оригинала:
, оригинал для третьего слагаемого находим по теореме об интегрировании оригинала:  .
.

 .
.
2. 
 по теореме о дифференцировании изображения.
по теореме о дифференцировании изображения.
3. 
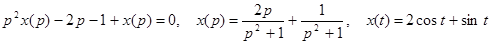
4. 
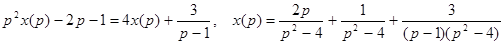
 .
.
Если свертку вычислить трудно, то можно найти оригинал  для последнего слагаемого по теореме разложения.
для последнего слагаемого по теореме разложения.
 =
= .
.
Решение дифференциальных уравнений с помощью интеграла Дюамеля.
Задано дифференциальное уравнение
 с нулевыми начальными условиями.
с нулевыми начальными условиями.
Известно решение уравнения  при
при  . Надо, используя это решение, найти решение для произвольной правой части.
. Надо, используя это решение, найти решение для произвольной правой части.
 ,
,
Следовательно,  . Отсюда по формуле интеграла Дюамеля
. Отсюда по формуле интеграла Дюамеля
 . Для вычисления выбирается одна из этих формул.
. Для вычисления выбирается одна из этих формул.
Решение систем дифференциальных уравнений методом операционного исчисления.
Задана система дифференциальных уравнений. Надо решить задачу Коши.
 .
.
Матричный способ решения.
Применим к обеим частям преобразование Лапласа
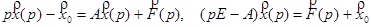

Теперь надо найти оригинал  для вектора
для вектора  .
.
Координатный способ решения.
Если обратную матрицу считать сложно, то можно применить преобразование Лапласа к каждому из уравнений системы, получить систему линейных алгебраических уравнений относительно изображений координат вектора  , решить ее. Затем надо найти оригиналы координат вектора.
, решить ее. Затем надо найти оригиналы координат вектора.
Примеры.
1.  Матричный способ
Матричный способ 
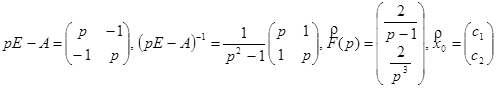
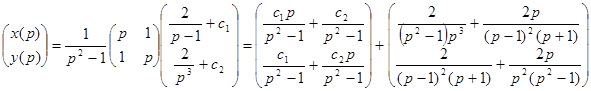
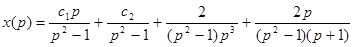
 - три раза применена теорема об интегрировании оригинала,
- три раза применена теорема об интегрировании оригинала,

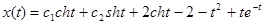
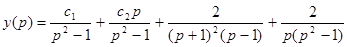
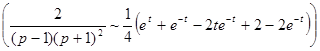
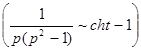
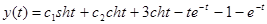
2. 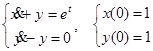
Координатный способ.
 ,
, 
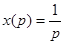
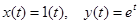
Примеры решения типовых домашних задач.
1. Найти изображение для оригинала  .
.
По теореме об интегрировании изображения  .
.
2. Найти оригинал по изображению 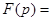
 .
.
По теореме об интегрировании оригинала  .
.
3. Найти оригинал по изображению  .
.
Особые точки функции  - полюсы первого порядка
- полюсы первого порядка  . По общей третьей теореме разложения (или второй теореме разложения)
. По общей третьей теореме разложения (или второй теореме разложения)
 .
.
4. Найти изображение периодического импульса с периодом 2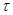

 .
. 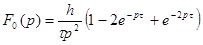

5. 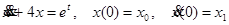
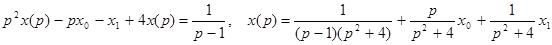
По третьей (или второй) теореме разложения
 ~
~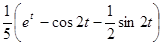 .
.
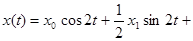
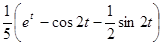
6. 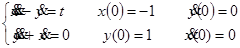
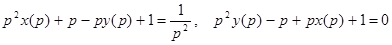
 ,
, 

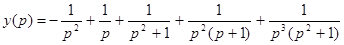
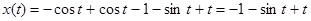
 .
.
7. 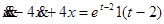
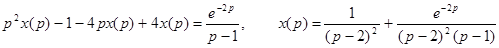
 ,
, 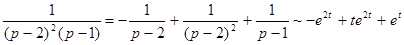
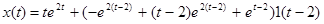
Дополнение
 -функция, преобразование Лапласа
-функция, преобразование Лапласа  -функции и ее разложение в ряд Фурье.
-функции и ее разложение в ряд Фурье.
| Определим |
|
 -функция не является обычной функцией, это – обобщенная функция,
-функция не является обычной функцией, это – обобщенная функция,  .
.
Если функцию Хевисайда 1(t)= можно интерпретировать как единичный скачок,
можно интерпретировать как единичный скачок,
то  -функцию можно считать единичным импульсом (единичным в смысле площади под графиком функции). Эти понятия используются в теории автоматического управления, в кибернетике. Можно считать, что
-функцию можно считать единичным импульсом (единичным в смысле площади под графиком функции). Эти понятия используются в теории автоматического управления, в кибернетике. Можно считать, что  .
.
Справедливо «фильтрующее свойство  - функции»
- функции»  .
.
Интеграл представляет собой «фильтр», который пропускает то значение функции, при котором аргумент  - функции обращается в нуль. На этом свойстве, которое доказывается в теории обобщенных функций, базируются, фактически, все применения
- функции обращается в нуль. На этом свойстве, которое доказывается в теории обобщенных функций, базируются, фактически, все применения  -функции.
-функции.
Преобразование Лапласа  -функции.
-функции.
 .
.
Как видно, обычными изображениями эти выражения не являются, так как не выполнено необходимое условие изображения.
В лекции "4.3 Моголы" также много полезной информации.
Разложение  -функции в ряд Фурье.
-функции в ряд Фурье.
Разложим  -функцию в ряд Фурье как функцию, заданную на отрезке
-функцию в ряд Фурье как функцию, заданную на отрезке  .
.
 .
.
 .
.



 . Заметим, что
. Заметим, что  .
.  .
.