Обобщенный метод наименьших квадратов

7.4. Обобщенный метод наименьших квадратов

Рассмотрим теперь модели, в которых переменные отклика коррелированные или они имеют разные дисперсии, так что С(y)≠s²I. В статистическом линейном моделировании большие значения фактора x_i могут приводить к большим значениям дисперсии D(y_i) переменной отклика. В любой простой или множественной регрессии, если значения переменных y₁, y₂, ..., y_п отклика получаются в следующие один за другим моменты времени, то они, как правило, коррелированы. Для случаев, где допущение С(y)=s²I не соблюдается, используется следующая линейная модель

у=Xw+e                                                        (7.4.1)

с соответствующими допущениями Е(у)=Xw, Е(e)=0 и С(y)=С(e)=S=s_к²V, где X - матрица модели полного ранга, w - вектор параметров модели и V - известная положительно определённая матрица. Матрица V размеров nxn имеет п² элементов и, если она неизвестна, то её элементы не могут быть оценены по выборке из п значений переменных отклика. В некоторых случаях (см. пример 7.4.1) предполагается простая структура матрицы V, что позволяет её оценить.

Оценка параметров модели и дисперсии при наличии ковариаций

В следующей теореме приводится оценка вектора w параметров модели (7.4.1) и дисперсии s_к².

Теорема 7.4.1. Пусть для модели у=Xw+e справедливы допущения Е(у)=Xw, Е(e)=0 и С(y)=С(e)=s_к²V, где X - матрица полного ранга и V - известная положительно определённая матрица. Тогда для этой модели:

1. Наилучшая линейная несмещённая оценка вектора w выполняется по формуле

=(X^ТV^–1X)^–1X^ТV^–1y.                                              (7.4.2)

1. Математическое ожидание вектора этой оценки Е()=w.
2. Матрица ковариаций вектора  имеет вид

С()=s_к²(X^ТV^–1X)^–1.                                                           (7.4.3)

1. Несмещённая оценка дисперсии s_к² делается с использованием выражения

Рекомендуемые материалы

s_к²= (у–X)^ТV^–1(у–X)/(n–р)                                             (7.4.4)

=у^Т[V^–1–V^–1X(X^ТV^–1X)^–1X^ТV^–1]у/(n–р),                   (7.4.5)

где вектор  находится по формуле (7.4.2).

Доказательство:

1. Так как матрица V положительно определённая, то при разложении Холецкого существует невырожденная матрица Р размеров nxn, так что V=PP^Т [Rao, Rao (1998) cтр.173]. Умножая модель у=Xw+e слева на Р^–1, получаем Р^–1у=Р^–1Xw+Р^–1e. При этом математическое ожидание E(Р^–1e)=Р^–1E(e)=Р^–10=0 и ковариационная матрица

С(Р^–1e) =Р^–1С(e)(Р^–1)^Т          [в силу (3.6.10)]

=Р^–1s_к²V(Р^–1)^Т

=s_к²Р^–1PP^Т(Р^–1)^Т

=s_к²I.

Таким образом, для модели Р^–1у=Р^–1Xw+Р^–1e соблюдаются допущения теоремы 7.2.4 Гаусса-Маркова и получаемый методом наименьших квадратов вектор

=[(Р^–1X)^Т(Р^–1X)]^–1(Р^–1X)^ТР^–1y

даёт наилучшую линейную несмещённую оценку параметров модели. По теоремам П.2.2 и П.5.2 его можно записать в виде

=[X^Т(Р^–1)^ТР^–1X]^–1X^Т(Р^–1)^ТР^–1y

=[X^Т(Р^Т)^–1Р^–1X]^–1X^Т(Р^Т)^–1Р^–1y          [в силу (П.5.4)]

=[X^Т(PР^Т)^–1X]^–1X^Т(PР^Т)^–1y               [в силу (П.5.5)]

=(X^ТV^–1X)^–1X^ТV^–1y.

1. Математическое ожидание вектора оценки

Е()=(X^ТV^–1X)^–1X^ТV^–1Е(y)

=(X^ТV^–1X)^–1X^ТV^–1Xw

=w.

1. Как и по теореме 7.2.3, вектора  оценки имеет ковариационную матрицу

С()=С[(X^ТV^–1X)^–1X^ТV^–1y]

=(X^ТV^–1X)^–1X^ТV^–1С(у)[(X^ТV^–1X)^–1X^ТV^–1]^Т  [в силу (3.6.10)]

=(X^ТV^–1X)^–1X^ТV^–1(s_к²V)V^–1X(X^ТV^–1X)^–1

=s_к²(X^ТV^–1X)^–1X^ТV^–1X(X^ТV^–1X)^–1

=s_к²(X^ТV^–1X)^–1.

1. Сумма квадратов остатков для модели Р^–1у=Р^–1Xw+Р^–1e находится в виде

S_Eк=(Р^–1у–Р^–1X)^Т(Р^–1у–Р^–1X)

=(у–X)^Т(Р^–1)^ТР^–1(у–X)

=(у–X)^Т(РР^Т)^–1(у–X)

=(у–X)^ТV^–1(у–X).

Следовательно по формуле (7.3.7) несмещённая оценка дисперсии находится так s_к²= (у–X)^ТV^–1(у–X)/(n–р). В выражении (у–X)^ТV^–1(у–X) раскроем скобки

(у–X)^ТV^–1(у–X)=у^ТV^–1(у–X)–^ТX^ТV^–1(у–X)

=у^ТV^–1у–у^ТV^–1X–^ТX^ТV^–1у+^ТX^ТV^–1X

и подставим =(X^ТV^–1X)^–1X^ТV^–1y и ^Т=у^ТV^–1X(X^ТV^–1X)^–1 чтобы получить

у^ТV^–1у–у^ТV^–1X(X^ТV^–1X)^–1X^ТV^–1y–у^ТV^–1X(X^ТV^–1X)^–1X^ТV^–1у+у^ТV^–1X(X^ТV^–1X)^–1X^ТV^–1y

=у^ТV^–1у–у^ТV^–1X(X^ТV^–1X)^–1X^ТV^–1y

=у^Т(V^–1–V^–1X(X^ТV^–1X)^–1X^ТV^–1)y.

Подставляя в (7.4.4) вместо (у–X)^ТV^–1(у–X) полученное выражение в правой части, получаем формулу (7.4.5).

□

Обычно говорят, что вектор =(X^ТV^–1X)^–1X^ТV^–1y оценки найден обобщённым методом наименьших квадратов. При этом заметим, поскольку матрица X полного ранга, то по теореме П.6.2 матрица X^ТV^–1X положительно определённая.

Математическое ожидание результата s_к² оценки находится по теореме 5.2.1. При этом используется допущение Е(y)=Xw и матрица А=V^–1–V^–1X(X^ТV^–1X)^–1X^ТV^–1, так что

Е(у^Т[V^–1–V^–1X(X^ТV^–1X)^–1X^ТV^–1]у)

=s_к²след[V^–1V–V^–1X(X^ТV^–1X)^–1X^ТV^–1V]+w^ТX^Т[V^–1–V^–1X(X^ТV^–1X)^–1X^ТV^–1]Xw

=s_к²след[I_n–V^–1X(X^ТV^–1X)^–1X^Т]+w^ТX^ТV^–1Xw–w^ТX^ТV^–1Xw

=s_к²[след(I_n–след(X^ТV^–1X(X^ТV^–1X)^–1)]

=s_к²[след(I_n)–след(I_р)]=s²(n–р).

Отсюда математическое ожидание Е(s_к²)= s_к²(n–р)/(n–р)=s_к².

Вектор оценки параметров модели по формуле (7.4.2) получается также и при допущении распределения переменных отклика по нормальному закону. Это доказывается в следующей теореме.

Теорема 7.4.2. Если вектор у имеет нормальное распределение N_n(Xw, s_к²V), где матрица X размеров пхр и ранга р, а V - известная положительно определённая матрица, то оценка максимального правдоподобия вектора w параметров и дисперсии s_к² делается соответственно по формулам

=(X^ТV^–1X)^–1X^ТV^–1y

и

_к²=(у–X)^ТV^–1(у–X)/п.

Доказательство: В данном случае функция правдоподобия имеет вид

L(w, s_к²)=ехр[–(у–Xw)^T(s_к²V)^–1(у–Xw)/2].

В силу (П.9.4), определитель det(s_к²V)=(s_к²)ⁿdet(V). Отсюда

L(w, s_к²)=ехр[–(у–Xw)^TV^–1(у–Xw)/(2s_к²)].

Формулы оценки для  и  могут быть получены взятием производных от ln[L(w, s_к²)] по q и s_к². Так, натуральный логарифм функции L(w, s_к²)

ln[L(w, s_к²)] =–n/2ln(2p)–n/2ln(s_к²)–1/2ln(detV)–(у–Xw)^TV^–1(у–Xw)/(2s_к²).

Раскроем скобки в последнем члене правой части последнего выражения, чтобы получить

(у^ТV^–1у–у^ТV^–1Xw–w^ТX^ТV^–1у+w^ТX^ТV^–1Xw)/(2s_к²).

Частные производные от ln[L(w,s_к²)] по w и s_к² получаются в виде

=–0–0–0–(0–2X^ТV^–1у+2X^ТV^–1Xw)/(2s_к²)

и

=–0–n/(2s_к²)–0+(у–Xw)^TV^–1(у–Xw)/[2(s_к²)²].

Приравнивая эти производные соответственно вектору 0 и числу 0, получаем выражения

X^ТV^–1Xw=X^ТV^–1у

и

s_к²=(у–Xw)^TV^–1(у–Xw)/n.                                        (7.4.6)

Первое из них является выражением нормальных уравнений и, так как матрица X^ТV^–1X положительно определённая, а, следовательно, невырожденная, то их решение даёт

=(X^ТV^–1X)^–1X^ТV^–1у.

Подставляя найденный вектор  оценки в выражение (7.4.6), находим оценку дисперсии

=(у–X)^TV^–1(у–X)/n.

Чтобы убедиться, что вектор  даёт максимальное значение функции L(w, s_к²) или её логарифма, возьмём вторую производную от ln[L(w, s_к²)] по w

=–X^ТV^–1X/s_к².

Матрица X^ТV^–1X положительно определённая, а матрица –X^ТV^–1X по определению в разделе П6 отрицательно определённая, следовательно, ln[L(w, s_к²)] при w= имеет максимальное значение. Также и для , если взять вторую производную от ln[L(w, s_к²)] по s_к², то имеем

=п/(2s_к⁴)–(у–Xq)^ТV^–1(у–Xq)/(s_к⁶)

=–п/(2s_к⁴). [в силу (7.4.6)]

Эта производная отрицательная, следовательно ln[L(w, s_к²)] при s_к²= тоже имеет максимальное значение.

□

Результат неверного допущения о виде ковариационной матрицы

Положим, что для модели (7.4.1) правильным допущением о ковариационной матрице является С(y)=s_к²V, но по ошибке (или намеренно) используется допущение С(y)=s²I. При этом вектор оценки находится обычным методом наименьших квадратов по формуле =(X^ТX)^–1X^Тy. В ней вектор оценки обозначен , чтобы отличать от наилучшей линейной несмещённой оценки по формуле =(X^ТV^–1X)^–1X^ТV^–1y обобщённого метода наименьших квадратов, которая должна использоваться в данном случае. Тогда математическое ожидание и матрица ковариаций вектора  получаются соответственно следующими:

E()= (X^ТX)^–1X^ТXw=w,                                           (7.4.7)

С()=s_к²(X^ТX)^–1X^ТVX(X^ТX)^–1.                                (7.4.8)

Отсюда видно, что при неправильном допущении о виде ковариационной матрицы оценка параметров обычным методом наименьших квадратов являются несмещённой, но матрица ковариаций отличается от данной выражением (7.4.3). По пункту 2 теоремы 7.4.1 дисперсии элементов вектора  в матрице ковариаций (7.4.8) не могут быть меньше дисперсий элементов вектора  в матрице ковариаций С()=s²(X^ТV^–1X)^–1. Это можно показать на следующем примере.

Пример 7.4.1. Положим, что имеется линейная модель у_i=w₀+w₁x_i+e_i, для которой D(у_i)=s_к²x_i и С(у_i, у_j) =0 при i≠j (i, j=1, 2, …, n). Таким образом, ковариационная матрица вектора у имеет вид

С(у)=s_к²V=s_к².

Это пример взвешенных наименьших квадратов, который относится обычно к случаю, когда матрица V диагональная с расположенными по диагонали значениями влияющей на отклик переменной. В этом случае матрица модели имеет вид

X=

и, в силу (7.4.2), имеем

==(X^ТV^–1X)^–1X^ТV^–1y

=.                      (7.4.9)

Матрица ковариаций вектора  дается выражением:

С()=s_к²(X^ТV^–1X)^–1

=.                      (7.4.10)

Если для оценки используется обычный метод наименьших квадратов, то вектор оценки =(X^ТX)^–1X^Тy, как дано в (7.2.2), а ковариационная матрица С() дается формулой (7.4.8), то есть,

С()=s_к²(X^ТX)^–1X^ТVX(X^ТX)^–1

=s_к²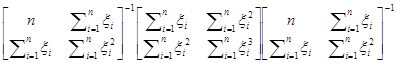

Обратите внимание на лекцию "12.4 Социально-экономическое развитие страны в пореформенный период".

=s_к²с, (7.4.11)

где с =1/. Дисперсия оценки  представлена правым нижним диагональным элементом матрицы в (7.4.11):

D() =s_к²,        (7.4.12)

а дисперсия оценки  дается соответствующим элементом выражения (7.4.10):

D() =.                              (7.4.13)

Рассмотрим следующие семь значений переменной x: 1, 2, 3, 4, 5, 6, 7. Используя формулу (7.4.12), получаем D()=0,1429s² и по формуле (7.4.13) имеем D() =0,1099s². Таким образом, как и ожидалось, для рассматриваемых значений переменной x использование обычного метода наименьших квадратов даёт оценку наклона с большей дисперсией.