Линейные преобразования функции модели
7.5. Линейные преобразования функции модели
Найденный обычным методом наименьших квадратов вектор  оценки параметров модели обладает тем свойством, что оцениваемые с его использованием ожидаемые значения переменных отклика
оценки параметров модели обладает тем свойством, что оцениваемые с его использованием ожидаемые значения переменных отклика  =
= +
+ xi1+
xi1+ xi2+…+
xi2+…+ xi(р–1) =xiс
xi(р–1) =xiс остаются тем же при простых линейных преобразованиях факторов. Значения этих факторов являются элементами строк xiс= [1, xi1, xi2,..., xi(р–1)] матрицы X модели. Пусть их преобразование делается по формуле uj=cjxj, то есть умножением на соответствующие определённые числа cj (j=1, 2, ..., р–1). Так строка xiс преобразуется в строку uiс=[1, c1xi1, c2xi2, ..., cр–1xi(р–1)]. В следующей теореме доказывается, что результат
остаются тем же при простых линейных преобразованиях факторов. Значения этих факторов являются элементами строк xiс= [1, xi1, xi2,..., xi(р–1)] матрицы X модели. Пусть их преобразование делается по формуле uj=cjxj, то есть умножением на соответствующие определённые числа cj (j=1, 2, ..., р–1). Так строка xiс преобразуется в строку uiс=[1, c1xi1, c2xi2, ..., cр–1xi(р–1)]. В следующей теореме доказывается, что результат  оценки ожидаемого значения переменной отклика на основе строки uiс является таким же, как и на основе строки xiс.
оценки ожидаемого значения переменной отклика на основе строки uiс является таким же, как и на основе строки xiс.
Теорема 7.5. Если xiс=[1, xi1, xi2,..., xi(р–1)] - строки матрицы X и uiс=[1, c1xi1, c2xi2,..., cр–1xi(р–1)] - строки матрицы U, то  =xiс
=xiс =uiс
=uiс , где
, где  =(UТU)–1UТy – вектор оценки методом наименьших квадратов вектора параметров модели с преобразованными факторами.
=(UТU)–1UТy – вектор оценки методом наименьших квадратов вектора параметров модели с преобразованными факторами.
Доказательство: Преобразование строки xiс в строку uiс можно записать в виде uiс=xiсD, где диагональная матрица D=диаг[1, c1, c2,..., cр–1]. В силу (П.2.22), вся матрица X преобразуется в матрицу U по формуле U=XD. Подставим U=XD в формулу оценки параметров  =(UТU)–1UТy чтобы получить
=(UТU)–1UТy чтобы получить
 =[(XD)Т(XD)]–1(XD)Тy
=[(XD)Т(XD)]–1(XD)Тy
=(XD)–1[(XD)Т]–1(XD)Тy
=D–1X–1(DТXТ)–1(XD)Тy
=D–1X–1(XТ)–1(DТ)–1DТXТy [в силу (П.5.5)]
=D–1(XТX)–1XТy
Рекомендуемые материалы
=D–1 , (7.5.1)
, (7.5.1)
где  - вектор оценки, вычисляемый по формуле (7.2.2). В результате имеем
- вектор оценки, вычисляемый по формуле (7.2.2). В результате имеем
 =uiс
=uiс =xiсDD–1
=xiсDD–1 =xiс
=xiс .
.
□
Следующим следствием теоремы 7.5 доказывается, что оценка ожидаемых значений переменных отклика остаётся неизменной и при любом линейном преобразовании полного ранга значений факторов в матрице модели.
Следствие 1. Результаты  оценки ожидаемых значений переменных отклика инвариантны к линейному преобразованию полного ранга значений факторов в матрице модели.
оценки ожидаемых значений переменных отклика инвариантны к линейному преобразованию полного ранга значений факторов в матрице модели.
Доказательство: Линейное преобразование матрицы X модели посредством матрицы полного ранга можно представить в виде
F=XK=[1, X1]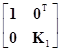
=[1+X10, 10Т+X1K1]
=[1, X1K1],
где X1 - матрица плана эксперимента
X1= (7.5.2)
(7.5.2)
и K1 – соответствующая невырожденная матрица. Здесь матрицы X и K разделены таким образом, чтобы преобразовать только элементы матрицы X1, оставляя первый столбец матрицы X неизменным. Как и при получении результата в выражении (7.5.1), вектор 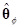 оценки параметров находится преобразованием вектора
оценки параметров находится преобразованием вектора  в виде
в виде
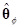 =(FТF)–1FТy
=(FТF)–1FТy
=K–1 . (7.5.3)
. (7.5.3)
Преобразование i-й строки матрицы X в i-ю строку матрицы F выполняется по формуле fiс=xiсK, а преобразование fiс в xiс в виде fiсK–1=xiс. Следовательно, результат  оценки ожидаемого значения i-й переменной отклика находится так
оценки ожидаемого значения i-й переменной отклика находится так
 =fiс
=fiс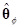
=fiсK–1
=xiс . (7.5.4)
. (7.5.4)
Поэтому произведения fiс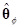 и xiс
и xiс дают один и то же результат
дают один и то же результат  , что и указывает на его инвариантность к линейному преобразованию полного ранга значений факторов в матрице модели.
, что и указывает на его инвариантность к линейному преобразованию полного ранга значений факторов в матрице модели.
□
В дополнение к результатам  оценки ожидаемых значений переменных отклика результат s2 оценки дисперсии также инвариантен к линейным преобразованиям факторов. В силу (7.5.4), результаты
оценки ожидаемых значений переменных отклика результат s2 оценки дисперсии также инвариантен к линейным преобразованиям факторов. В силу (7.5.4), результаты  оценки ожидаемых значений переменных отклика инвариантны к линейным преобразованиям факторов. Поэтому их вектор
оценки ожидаемых значений переменных отклика инвариантны к линейным преобразованиям факторов. Поэтому их вектор  =X
=X тоже инвариантен к линейным преобразованиям значений факторов. Оценка дисперсии делается по формуле s2= (у–X
тоже инвариантен к линейным преобразованиям значений факторов. Оценка дисперсии делается по формуле s2= (у–X )Т(у–X
)Т(у–X )/(n–р), поэтому и её результат инвариантен к линейным преобразованиям значений факторов.
)/(n–р), поэтому и её результат инвариантен к линейным преобразованиям значений факторов.
Статистики, имеющие распределения t и F, а также статистика R2 тоже инвариантны к линейным преобразованиям значений переменных отклика или факторов, но не к совместному линейному преобразованию переменных отклика и факторов.
Модель с центрированной функцией
Для каждого из n опытов эксперимента модель (7.1.2) можно записать с центрированной функцией путём центрирования значений факторов их усреднёнными значениями в виде
yi=q0+q1xi1+q2xi2+…+qр–1xi(р–1)+ei,
=qc+q1(xi1– )+q2(xi2–
)+q2(xi2– )+…+qр–1(xi(р–1)–
)+…+qр–1(xi(р–1)– )+ei, (7.5.5)
)+ei, (7.5.5)
где  =
= /n (j=1, 2, ..., р–1) и
/n (j=1, 2, ..., р–1) и
qc=q0+q1 +q2
+q2 +...+qр–1
+...+qр–1 . (7.5.6)
. (7.5.6)
Для вектора уТ=[у1, у2, ..., уп] переменных отклика модель (7.5.5) с центрированной функцией в матричном виде записывается так
у=[1, Xc] +e, (7.5.7)
+e, (7.5.7)
где q1T= [q1, q2,..., qр–1],
Xc=(I–Е/n)X1
= , (7.5.8)
, (7.5.8)
и матрица X1 дана в (7.5.2). Матрицу I–Е/n иногда называют матрицей центрирования.
Как и в (7.2.5), нормальные уравнения для модели (7.5.7) записываются в виде
[1, Xc]Т[1, Xc] =[1, Xc]Тy. (7.5.9)
=[1, Xc]Тy. (7.5.9)
В силу (П.3.1) и (П.3.5), произведение [1, Xc]Т[1, Xc] в левой части преобразуется к виду
[1, Xc]Т[1, Xc]= [1, Xc]=
[1, Xc]=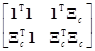
=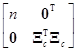 , (7.5.10)
, (7.5.10)
где 1ТXc=0Т, так как суммы элементов столбцов матрицы Xc равны нулю. Это легко проверить, сделав следующие преобразования
1ТXc=1Т(I–Е/n)X1=1Т(I–11Т/n)X1=(1Т–1Т11Т/n)X1=(1Т–1Т)X1=0Т.
Правую часть выражения (7.5.9) можно записать в виде
[1, Xc]Тy= y=
y=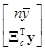 .
.
На основе сделанных преобразований оценка параметров модели (7.5.7) методом наименьших квадратов делается с использованием выражения в матричной форме
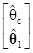 ={[1, Xc]Т[1, Xc]}–1[1, Xc]Тy=
={[1, Xc]Т[1, Xc]}–1[1, Xc]Тy=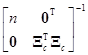
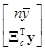
=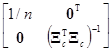
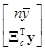 =
=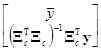
или отдельными формулами
 =
= (7.5.11)
(7.5.11)
и
 =(XcТXc)–1XcТy. (7.5.12)
=(XcТXc)–1XcТy. (7.5.12)
Эти формулы оценки являются такими же, как и формула  =(XТX)–1XТy оценки методом наименьших квадратов без центрирования факторов, но с корректировкой
=(XТX)–1XТy оценки методом наименьших квадратов без центрирования факторов, но с корректировкой
 =
= –
–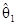
 –
–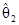
 –...–
–...–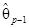
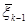
= –
– Т
Т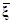 , (7.5.13)
, (7.5.13)
получаемой на основе выражения (7.5.6) для qc. Это можно продемонстрировать следующим образом. Если матрица X и вектор q разделены в виде X=[1, X1] и q= , то нормальные уравнения XТXq=XТy принимают вид
, то нормальные уравнения XТXq=XТy принимают вид
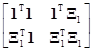
 =
=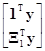 .
.
Из них получаем два выражения
пq0+1ТX1q1=п (7.5.14)
(7.5.14)
и
X1Т1q0+X1ТX1q1=X1Тy. (7.5.15)
Уравнение (7.5.14) после преобразования становится
q0+ q1=
q1= ,
,
где 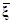 =X1Т1/п – вектор усреднённых значений факторов в опытах эксперимента. В силу (7.5.6), это уравнение принимает вид
=X1Т1/п – вектор усреднённых значений факторов в опытах эксперимента. В силу (7.5.6), это уравнение принимает вид  =
= . Выражение (7.5.15) можно записать так
. Выражение (7.5.15) можно записать так
п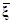 q0+X1ТX1q1=X1Тy. (7.5.16)
q0+X1ТX1q1=X1Тy. (7.5.16)
Представленные выражением (7.5.9) нормальные уравнения для модели с центрированной функцией могут быть записаны в форме
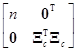
 =
=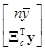 ,
,
что представляется также и в разделённом виде отдельными выражениями
nqс=n (7.5.17)
(7.5.17)
и
XcТXcq1=XcТy. (7.5.18)
Следовательно, уравнение (7.5.17) является тем же, что и уравнение (7.5.14).
В силу (7.3.8), имеем Xc=(I–Е/n)X1 и произведение XcТXc принимает вид
XcТXc=X1Т(I–Е/n)X1=X1ТX1–X1Т11ТX1/n=X1ТX1–n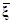
 .
.
Также можно получить, что
XcТy=X1Т(I–Е/n)y=X1Тy–X1Т11Тy/n=X1Тy–n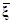
 .
.
Подставляя в (7.5.18) вместо XcТXc и XcТy полученные их выражения, имеем
X1ТX1q1–n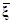
 q1=X1Тy–n
q1=X1Тy–n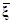

или
X1ТX1q1+n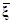 (
( –
– q1)=X1Тy.
q1)=X1Тy.
В силу (7.5.13),  –q1Т
–q1Т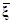 =q0, следовательно, выражение (7.5.18) является тем же самым, что и (7.5.16).
=q0, следовательно, выражение (7.5.18) является тем же самым, что и (7.5.16).
На примере применения обобщенного метода наименьших квадратов покажем, что для определённого вида ковариационной матрицы S результат оценки параметров получается тем же, что и для центрированной модели с применением обычного метода наименьших квадратов.
Пример 7.5.1. Рассмотрим модель с разделёнными матрицей X модели и вектором w её параметров вида
у=[1, X1] +e.
+e.
В матрице ковариаций
S=s2[(1–r)I+rЕ]=s2V (7.5.19)
= s2 ,
,
случайных переменных модели они все имеют одну и ту же дисперсию s2 и все пары переменных имеют одинаковую корреляцию r. Такое представление матрицы ковариаций предполагается для некоторых повторных измерений и случаев внутригрупповой корреляции. Определение коэффициента корреляции r дано выражением (3.2.14).
В силу (7.4.2), имеем
 =
= =(XТV–1X)–1XТV–1y.
=(XТV–1X)–1XТV–1y.
Для разделённой матрицы X=[1, X1] матрица XТV–1X в разделённом виде записывается так
XТV–1X= V–1[1, X1]
V–1[1, X1]
= .
.
Обратная матрицы V=(1–r)I+rЕ размеров пхп задается выражением [Rencher, Schaalje (2008) cтр.176]
V–1=а(I–brЕ), (7.5.20)
где а=1/(1–r) и b=1/[1+(п–1)r]. Используя выражение (7.5.20) для V–1, матрица XТV–1X принимает вид
XТV–1X= (7.5.21)
(7.5.21)
и также
XТV–1у= . (7.5.22)
. (7.5.22)
Отсюда получаем
 =(XТV–1X)–1XТV–1y
=(XТV–1X)–1XТV–1y
= ,
,
являющееся тем же, что и в выражениях (7.5.11) и (7.5.12) для модели в центрированном виде. Таким образом, оценка обычным методом наименьших квадратов является наилучшей линейной несмещённой оценкой при ковариационной матрице с равными дисперсиями и равными коэффициентами корреляции.
□
Когда вектор  оценки ожидаемых значений переменных отклика выражается через факторы, представленные в центрированной форме, то имеем
оценки ожидаемых значений переменных отклика выражается через факторы, представленные в центрированной форме, то имеем
 =[1, Xc]
=[1, Xc]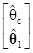
=1 +Xc(XcТXc)–1XcТy. (7.5.23)
+Xc(XcТXc)–1XcТy. (7.5.23)
Выражение суммы квадратов остатков для модели с центрированной функцией имеет вид
SE= –
– ТXcТy, (7.5.24)
ТXcТy, (7.5.24)
оказываясь тем же, что и SE=yТy– ТXТy для обычной модели. Это можно показать, сделав следующие преобразования:
ТXТy для обычной модели. Это можно показать, сделав следующие преобразования:
yТy– ТXТy=yТy–[
ТXТy=yТy–[ ,
,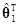 ][1, X1]Тy
][1, X1]Тy
=yТy–[ ,
,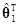 ]
]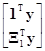
=yТy– n
n –
–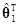 X1Тy
X1Тy
=yТy–( –
–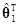
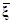 )n
)n –
–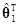 X1Тy [в силу (7.3.13)]
X1Тy [в силу (7.3.13)]
=yТy–n –
–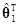 (X1Тy–n
(X1Тy–n
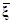 )
)
= –
–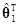 XcТy.
XcТy.
Таким образом, оценка дисперсии для модели с центрированной функцией остаётся такой же, как и для обычной модели.
Модель с нормированной функцией
Для каждого опыта эксперимента модель (7.5.5) можно записать с использованием центрированных и линейно преобразованных или нормированных факторов в виде
yi=b0+b1(xi1– )/S1+b2(xi2–
)/S1+b2(xi2– )/S2+…+bр–1(xi(р–1)–
)/S2+…+bр–1(xi(р–1)– )/Sр–1+ei, (7.5.25)
)/Sр–1+ei, (7.5.25)
где Sj2= (j=1, 2, …, р–1) - значения вторых моментов факторов в опытах эксперимента относительно их усреднённых
(j=1, 2, …, р–1) - значения вторых моментов факторов в опытах эксперимента относительно их усреднённых  [Box, Wilson (1951) стр.9; Box (1952)]. Модель в таком виде имеет нормированную функцию и широко используется для анализа результатов планируемых экспериментов. Состоящую из нормированных факторов матрицу плана эксперимента легче анализировать, и она более удобна для расчётов, чем матрица плана в исходных значениях факторов.
[Box, Wilson (1951) стр.9; Box (1952)]. Модель в таком виде имеет нормированную функцию и широко используется для анализа результатов планируемых экспериментов. Состоящую из нормированных факторов матрицу плана эксперимента легче анализировать, и она более удобна для расчётов, чем матрица плана в исходных значениях факторов.
Вышеуказанное нормирование применяется в случаях, когда в опытах эксперимента факторы устанавливаются при многих значениях. Однако если они устанавливаются только при двух значениях, то их нормирование возможно по формуле (2.6.4). При двух, то есть большем x+ и меньшем x– значениях фактора, эта формула принимает вид
x=[x–(x++x–)/2]/(x+–x–)/2.
Формула нормирования фактора, принимающего в опытах многие значения, имеет вид
x=(ξ– )/S,
)/S,
где  =
= , S=
, S= и m – число значений фактора x. Две эти формулы нормирования одинаковы, когда
и m – число значений фактора x. Две эти формулы нормирования одинаковы, когда  =(x++x–)/2 и
=(x++x–)/2 и  =(x+–x–)/2. Отсюда имеем
=(x+–x–)/2. Отсюда имеем  =(x+–x–)/2 и, возводя в квадрат обе части этого равенства, получаем
=(x+–x–)/2 и, возводя в квадрат обе части этого равенства, получаем  =m[(x+–x–)/2]2. Это равенство соблюдается только тогда, когда переменная ξ принимает два значения x+ и x–.
=m[(x+–x–)/2]2. Это равенство соблюдается только тогда, когда переменная ξ принимает два значения x+ и x–.
В силу (5.1.2), числитель выражения для Sj2 можно записать в виде квадратичной формы
 =xjТ(I–Е/n)xj,
=xjТ(I–Е/n)xj,
откуда Sj=[xjТ(I–Е/n)xj/n]1/2. Для всех столбцов x1, x2, ..., xр–1 матрицы X1 плана эксперимента в исходных значениях факторов можно получить диагональную матрицу
Ds=диаг{[x1Т(I–Е/n) x1/n]1/2, [x2Т(I–Е/n)x2/n]1/2, …, [xр–1Т(I–Е/n)xр–1/n]1/2},
которая имеет вид Ds= и ей обратную Ds–1=
и ей обратную Ds–1= . Следовательно, для переменных у1, у2, ..., уп отклика модель (7.5.25) в матричной форме принимает вид
. Следовательно, для переменных у1, у2, ..., уп отклика модель (7.5.25) в матричной форме принимает вид
у=[1, X1] +e, (7.5.26)
+e, (7.5.26)
где b1T= [b1, b2,..., bр–1],
X1=(I–Е/n)X1Ds–1 (7.5.27)
= ,
,
и исходная матрица X1 дана в (7.5.2). Матрицы I–Е/n и Ds–1 невырожденные и выполняют элементарные преобразования столбцов матрицы X1. Следовательно, матрица X1 эквивалентна матрице X1 [Seber (2008) стр. 330].
Как и в (7.2.5), нормальные уравнения для модели (7.5.26) записываются в виде
[1, X1]Т[1, X1] =[1, X1]Тy. (7.5.28)
=[1, X1]Тy. (7.5.28)
В силу (П.3.1) и (П.3.5), произведение [1, X1]Т[1, X1] в левой части преобразуется так
[1, X1]Т[1, X1]= [1, X1]=
[1, X1]=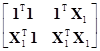
= , (7.5.29)
, (7.5.29)
так как 1Т1=n и 1ТX1=1Т(I–Е/n)X1Ds–1=(1Т–1Т11Т/n)X1Ds–1=0ТX1Ds–1=0Т. Правую часть выражения (7.5.28) можно записать в виде
[1, X1]Тy= y=
y=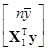 .
.
На основании этих преобразований оценка параметров модели методом наименьших квадратов даётся матричным выражением
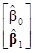 ={[1, X1]Т[1, X1]}–1[1, X1]Тy=
={[1, X1]Т[1, X1]}–1[1, X1]Тy=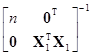
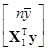
=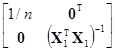
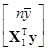 =
=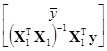
или отдельными формулами
 =
= (7.5.30)
(7.5.30)
и
 =(X1ТX1)–1X1Тy. (7.5.31)
=(X1ТX1)–1X1Тy. (7.5.31)
Вектор оценки ожидаемых значений переменных отклика находится по формуле
 =[1, X1]
=[1, X1]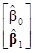
=1 +X1(X1ТX1)–1X1Тy. (7.5.32)
+X1(X1ТX1)–1X1Тy. (7.5.32)
В силу (7.5.8) и (7.5.27), имеем X1=XcDs–1 и, подставляя это в (7.5.32), получаем
 =1
=1 +XcDs–1(Ds–1XcТXcDs–1)–1Ds–1XcТy
+XcDs–1(Ds–1XcТXcDs–1)–1Ds–1XcТy
=1 +XcDs–1Ds(XcТXc)–1DsDs–1XcТy
+XcDs–1Ds(XcТXc)–1DsDs–1XcТy
=1 +Xc(XcТXc)–1XcТy. (7.5.33)
+Xc(XcТXc)–1XcТy. (7.5.33)
Таким образом, вектор оценки ожидаемых значений переменных отклика получается тем же самым, что и в (7.5.23) для модели с центрированной функцией. Следовательно, все результаты, полученные для модели с центрированными факторами справедливы и для модели с нормированными факторами.
В теории планирования экспериментов и методологии функций отклика принято пользоваться линейной моделью с нормированными факторами [Box, Draper (2007); Myers с соавт. (2016)]. Эта модель имеет вид
у=Хb+e, (7.5.34)
где Х=[1, X1] и b= . Сумма квадратов остатков для этой модели находится по формуле
. Сумма квадратов остатков для этой модели находится по формуле
SE=(у–X )Т(у–X
)Т(у–X )
)
=yТy– ТXТy.
ТXТy.
Скорректированная усреднённым значением переменных отклика эта сумма принимает вид
SE=yТy–[ ,
, Т][1, X1]Тy
Т][1, X1]Тy
=yТy–[ ,
, Т]
Т]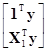
=yТy– n
n –
– ТX1Тy
ТX1Тy
=yТy–n –
– ТX1Тy
ТX1Тy
= –
– ТX1Тy. [в силу (5.1.1)] (7.5.35)
ТX1Тy. [в силу (5.1.1)] (7.5.35)
В ней член  ТX1Тy преобразуется так
ТX1Тy преобразуется так
 ТX1Тy=yТX1(X1ТX1)–1X1Тy
ТX1Тy=yТX1(X1ТX1)–1X1Тy
=yТXc(XcТXc)–1XcТy
=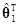 XcТy.
XcТy.
Следовательно, сумма квадратов остатков для модели с нормированной функцией такая же, как для модели с центрированной функцией в (7.5.24) и исходной модели в (7.3.10).
Упражнения
7.1. Покажите, что в (7.2.3) сумма  =(у–Xq)Т(у–Xq).
=(у–Xq)Т(у–Xq).
7.2. Покажите, что (7.2.7) получается из (7.2.6). Почему матрица XТX положительно определённая?
7.3. Получите ковариационную матрицу С( ) в (7.2.12) из (7.2.11).
) в (7.2.12) из (7.2.11).
7.4. Покажите, что в примере 7.2.2 дисперсия D( )=s2(
)=s2( )/
)/ такая же, как дисперсия D(
такая же, как дисперсия D( ) в (6.2.13).
) в (6.2.13).
7.5. Покажите, что произведение AAТ в доказательстве теоремы 7.2.4 может быть представлено в виде AAТ=[А–(XТX)–1XТ][А–(XТX)–1XТ]Т+(XТX)–1.
7.6. Докажите следствие 1 теоремы 7.2.4, используя описанный в конце раздела П.14 метод множителей Лагранжа.
7.7. Проверьте (7.5.3) в доказательстве следствия 1 теоремы 7.5.
7.8. Покажите, что (у–X )Т(у–X
)Т(у–X )=yТy–
)=yТy– ТXТy, как в (7.3.8).
ТXТy, как в (7.3.8).
7.9. Покажите, что E(SE) =s2(n–р), как и в теореме 7.3.2, используя следующий подход. Покажите, что SE=yТy– ТXТX
ТXТX . Покажите, что Е(yТy) =ns2+qТXТXq и Е(
. Покажите, что Е(yТy) =ns2+qТXТXq и Е( ТXТX
ТXТX )=рs2+qТXТXq.
)=рs2+qТXТXq.
7.10. Покажите, что нецентрированную модель можно записать в центрированном виде (7.5.5) с qc определенным выражением (7.5.6).
7.11. Покажите, что Xс=(I–Е/n)X1 как в (7.5.8), где X1, как показано в (7.5.2).
7.12. Покажите, что оценки  =
= в (7.5.11) и
в (7.5.11) и  =(XcТXc)–1XcТy в (7.5.12) такие же, как
=(XcТXc)–1XcТy в (7.5.12) такие же, как  =(XТX)–1XТy в (7.2.2), используя обратную матрицы XТX в разделённом виде:
=(XТX)–1XТy в (7.2.2), используя обратную матрицы XТX в разделённом виде:
(XТX)–1=[(1, X1)Т(1, X1)]–1.
7.13. Покажите, что в доказательстве теоремы 7.3.5 имеем
(у–Xq)Т(у–Xq)= (у–X )Т(у–X
)Т(у–X )+(
)+( –q)ТXТX(
–q)ТXТX( –q).
–q).
7.14. Объясните, почему после теоремы 7.3.5 отмечено, что функция f(y; q, s2) не разлагается на сомножители в виде g1( ,q)g2(
,q)g2( 2, s2)h(у).
2, s2)h(у).
7.15. Покажите, что для матрицы V=(1–r)I+rЕ выражения (7.5.19) матрица V–1=а(I–brЕ), где а =1/(1–r) и b=1/[1+(п–1)r], является обратной.
7.16. (а) Покажите, что XТV–1X= , как дано в (7.5.21).
, как дано в (7.5.21).
(б) Покажите, что XТV–1у= , как дано в (7.5.22).
, как дано в (7.5.22).
7.17. Покажите, что С( )=sк2(XТX)–1XТVX(XТX)–1 как и в (7.4.8), где
)=sк2(XТX)–1XТVX(XТX)–1 как и в (7.4.8), где  =(XТX)–1XТy и С(y)= sк2V.
=(XТX)–1XТy и С(y)= sк2V.
7.18. (а) Покажите, что по взвешенному мотоду наименьших квадратов при D(уi)=s2xi оценки параметров модели уi=w0+w1xi+ei находятся по формуле (7.4.9).
21 Аргентина 1980-1990-е гг. - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
(б) Проверьте выражение ковариационной матрицы С( ) в (7.4.10).
) в (7.4.10).
7.19. Получите выражение ковариационной матрицы С( ) в (7.4.11).
) в (7.4.11).
7.20. В качестве альтернативного вывода D( ) в (7.4.12) используйте следующие два шага, чтобы найти D(
) в (7.4.12) используйте следующие два шага, чтобы найти D( ) с помощью
) с помощью  =
= /
/ :
:
(а) Используя D(уi) =s2xi, покажите, что D( ) =s2
) =s2 xi/[
xi/[ ]2.
]2.
(б) Покажите, что это выражение для D( ) равно тому, что в (7.4.12).
) равно тому, что в (7.4.12).
7.21. Используя x =2, 3, 5, 7, 8, 10, сравните D( ) в (7.4.12) с D(
) в (7.4.12) с D( ) в (7.4.13).
) в (7.4.13).























