Доверительные интервалы и области
6.5. Доверительные интервалы и области
Доверительные интервалы параметров модели
В разделе 1.5 показано, что нормированная случайная переменная имеет распределение N(0, 1), то есть, распределена по стандартному нормальному закону со средним равным 0 и дисперсией s2=1. Следовательно, если провести нормирование случайных переменных  и
и  , то получаются нормированные случайные переменные
, то получаются нормированные случайные переменные  и
и  , имеющие стандартное нормальное распределение N(0, 1). А если в выражения (6.2.11) и (6.2.10) дисперсий D(
, имеющие стандартное нормальное распределение N(0, 1). А если в выражения (6.2.11) и (6.2.10) дисперсий D( ) и D(
) и D( ) оценок параметров вместо s2 подставить её оценку s2 из выражения (6.2.11), то случайные переменные
) оценок параметров вместо s2 подставить её оценку s2 из выражения (6.2.11), то случайные переменные  и
и  , как и в разделе 1.10, приобретают распределение t с п–2 степенями свободы.
, как и в разделе 1.10, приобретают распределение t с п–2 степенями свободы.
Определим tα,L(п–2) и tα,U(п–2), соответственно, нижним и верхним предельными значениями распределения t(п–2) [Searle (1971) стр. 107]. Сумма вероятностей, что статистика t* меньше или равна нижнему пределу и больше или равна верхнему пределу
Pr[t*≤ta,L(п–2)]+Pr[t*≥ta,U(п–2)]=α.
Отсюда для имеющей распределение t(п–2) статистики t* получаем вероятность
Pr[ta,L(п–2)≤t*≤ta,U(п–2)]=1–α. (6.5.1)
Случайные переменные  и
и  тоже имеют распределение t(п–2), поэтому можно записать
тоже имеют распределение t(п–2), поэтому можно записать
Pr[tα,L(п–2)≤ ≤tα,U(п–2)]=1–α
≤tα,U(п–2)]=1–α
Рекомендуемые материалы
и
Pr[tα,L(п–2)≤ ≤tα,U(п–2)]=1–α.
≤tα,U(п–2)]=1–α.
Преобразование этих вероятностных выражений приводит к следующим неравенствам:
Pr[ –stα,U(п–2)
–stα,U(п–2) ≤ q0≤
≤ q0≤ –stα,L(п–2)
–stα,L(п–2) ]=1–α
]=1–α
и
Pr[ –stα,U(п–2)
–stα,U(п–2) ≤q1≤
≤q1≤ –stα,L(п–2)
–stα,L(п–2) ]=1–α.
]=1–α.
Эти неравенства дают 100(1–α)% доверительные интервалы для q0 и q1 соответственно между меньшими и большими значениями
 –stα,U(п–2)
–stα,U(п–2) ,
,  –stα,L(п–2)
–stα,L(п–2) , (6.5.2)
, (6.5.2)
и
 –stα,U(п–2)
–stα,U(п–2) ,
,  –stα,L(п–2)
–stα,L(п–2) . (6.5.3)
. (6.5.3)
Для этих доверительных интервалов часто требуется, чтобы они были симметричны по отношению к  и
и  , а для этого необходимо
, а для этого необходимо
–tα,L(п–2)=+tα,U(п–2)=tα/2(п–2), где вероятность Pr[t*≥tα/2(п–2)]=α/2. (6.5.4)
Поэтому меньшие и большие предельные значения интервалов (6.5.2) и (6.5.3) находятся по формулам
 ±stα/2(п–2)
±stα/2(п–2) (6.5.5)
(6.5.5)
и
 ±stα/2(п–2)
±stα/2(п–2) . (6.5.6)
. (6.5.6)
Они имеют длины 2stα/2(п–2) и 2stα/2(п–2)
и 2stα/2(п–2) .
.
Доверительные области параметров
Доверительные интервалы полученного типа легко вычисляются и полезны, но они не принимают во внимание корреляцию между оценками параметров. Эта корреляция или зависимость между оценками большая, если столбцы матрицы модели в значительной степени не ортогональны.
Чтобы пояснить влияние корреляции рассмотрим совместную оценку параметров модели, имеющей две влияющие на отклик переменные. В ней переменную отклика и влияющие на неё переменные x1 и x2 подвергнем нормированию. При этом уравнение модели принимает вид
ун=1b0+b1х1+b2х2+eн. (6.5.7)
Для оценки параметров этой модели используем часть данных таблицы 7.1 главы 7 из опытов 1, 2, 3 и 4. В этих опытах переменные x1 и x2 устанавливались только при двух значениях, следовательно, как показано в разделе 6.2, этим достигается минимальная дисперсия оценки параметров модели. Нормирование значений переменных отклика выполним по формуле унi=(уi– )/S, где S=
)/S, где S= - натуральное стандартное отклонение, как определено в разделе 1.4, а нормирование значений переменных x1 и x2 выполнялось по формуле (2.6.4). Рассматриваемые данные для модели (6.5.7) представлены в левой части таблицы 6.5.1.
- натуральное стандартное отклонение, как определено в разделе 1.4, а нормирование значений переменных x1 и x2 выполнялось по формуле (2.6.4). Рассматриваемые данные для модели (6.5.7) представлены в левой части таблицы 6.5.1.
Дисперсия нормированных переменных отклика ун равна 1. Матрица модели в этом случае Х= . Все её столбцы ортогональны друг другу. Оценка параметров модели (6.5.7) выполняется по формуле
. Все её столбцы ортогональны друг другу. Оценка параметров модели (6.5.7) выполняется по формуле  =(ХТХ)–1ХТун. А, если для модели с нормированными переменными дисперсия sн2=1, то дисперсионная матрица вектора
=(ХТХ)–1ХТун. А, если для модели с нормированными переменными дисперсия sн2=1, то дисперсионная матрица вектора  оценки параметров имеет вид (ХТХ)–1=
оценки параметров имеет вид (ХТХ)–1= .
.
Таблица 6.5.1. Данные коэффициента (у) усиления транзистора и переменных x1 и x2
| Столбцы х1 и х2 ортогональны | Столбцы х1* и х2* не ортогональны | ||||||||||||
| Опыт | x1 | x2 | у | х1 | х2 | ун | Опыт | x1 | x2 | у | х1* | х2* | уп* |
| 1 | 195 | 4,00 | 1004 | –1 | +1 | +1,364 | 1 | 195 | 4,00 | 1004 | –1.576 | –1,026 | –1,480 |
| 2 | 255 | 4,00 | 1636 | +1 | +1 | +0,551 | 6 | 255 | 4,10 | 1270 | +0.864 | –0,653 | +0,692 |
| 3 | 195 | 4,60 | 852 | +1 | –1 | –0,930 | 11 | 255 | 4,70 | 1146 | +0.864 | +1,585 | –0,320 |
| 4 | 255 | 4,60 | 1506 | –1 | –1 | –0,986 | 14 | 230 | 4,30 | 1321 | –0.152 | +0.093 | +1,108 |
В данном случае доверительные интервалы параметров β1 и β2 могут быть найдены по статистике, имеющей распределение хи-квадрат. Разности β1– и β2–
и β2– имеют нулевые математические ожидания Е(β1–
имеют нулевые математические ожидания Е(β1– )=β1–Е(
)=β1–Е( )=β1–β1=0 и Е(β2–
)=β1–β1=0 и Е(β2– )
)
=β2–Е( )=β2–β2=0. Из дисперсионной матрицы вектора
)=β2–β2=0. Из дисперсионной матрицы вектора  видно, что дисперсии всех оценок равны 1/4. Поэтому, умножая разности β1–
видно, что дисперсии всех оценок равны 1/4. Поэтому, умножая разности β1– и β2–
и β2– на 4, получаем их дисперсии равные 1. Отсюда, по данному в разделе 5.3 определению, переменные 4(β1–
на 4, получаем их дисперсии равные 1. Отсюда, по данному в разделе 5.3 определению, переменные 4(β1– )2 и 4(β2–
)2 и 4(β2– )2 имеют распределения хи-квадрат с одной степенью свободы. Соответствующее вероятности 0,95 критическое значение для этого распределения с одной степенью свободы равно 3,841. Следовательно, зная значения
)2 имеют распределения хи-квадрат с одной степенью свободы. Соответствующее вероятности 0,95 критическое значение для этого распределения с одной степенью свободы равно 3,841. Следовательно, зная значения  =0,977 и
=0,977 и  =0,214 и решая уравнения
=0,214 и решая уравнения
4(β1– )2=3,841 и 4(β2–
)2=3,841 и 4(β2– )2=3,841 (6.5.8)
)2=3,841 (6.5.8)
относительно β1 и β2, можно найти индивидуальные доверительные интервалы для этих параметров. Для данных таблицы 6.5.1 с ортогональными столбцами х1 и х2 они получаются следующие: для β1 доверительный интервал 0,977±0,980 длиной 1,960 и для β2 доверительный интервал 0,214±0,980 тоже длиной 1,960.
Совместная доверительная область параметров b1 и b2 может быть найдена также по имеющей распределение хи-квадрат статистике. Из дисперсионной матрицы вектора  оценки параметров видно, что все оценки распределены независимо. Следовательно, и разности β1–
оценки параметров видно, что все оценки распределены независимо. Следовательно, и разности β1– и β2–
и β2– тоже распределены независимо, а при умножении на 4 их дисперсии становятся равными 1. Отсюда по определению распределения хи-квадрат сумма
тоже распределены независимо, а при умножении на 4 их дисперсии становятся равными 1. Отсюда по определению распределения хи-квадрат сумма
4(β1– )2+4(β2–
)2+4(β2– )2~χ2(2) (6.5.9)
)2~χ2(2) (6.5.9)
имеет распределение хи-квадрат с 2 степенями свободы. Критическое значение для этого распределения, соответствующее вероятности 0,95 и 2 степеням свободы, равно 5,991. Следовательно, круговая совместная 95% доверительная область параметров b1 и b2 с центром в точке ( ,
,  ) состоит из всех точек с координатами (b1,b2) определяемыми значениями параметров b1 и b2, так что
) состоит из всех точек с координатами (b1,b2) определяемыми значениями параметров b1 и b2, так что
4(β1–0,977)2+4(β2–0,214)2≤5,991. (6.5.10)
Совместная область и индивидуальные интервалы параметров b1 и b2 показаны на Рис.6.5.1.
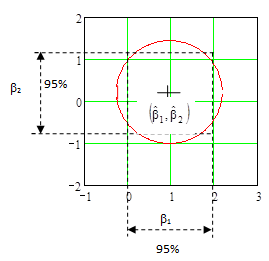
Рис.6.5.1. 95% совместная доверительная область и доверительные интервалы при ортогональном плане эксперимента
Теперь используем представленные в правой части таблицы 6.5.1 данные опытов 1, 6, 11 и 14 таблицы 7.1. В этих опытах переменные x1 и x2 устанавливались при более чем двух значениях, следовательно, в этом случае невозможно получить минимальную дисперсию оценки параметров модели. Нормирование значений переменной отклика и переменных x1 и x2 в данном случае необходимо выполнять так же, как это делалось со значениями переменной отклика в левой части таблицы. При этом уравнение модели в нормированных переменных принимает вид
ун*=1b0+b1*х1*+b2*х2*+eн*. (6.5.11)
Дисперсия нормированной переменной отклика ун* в этом случае тоже равна 1, но матрица модели Х*= . При таком нормировании, как и для данных в левой части таблицы, столбцы значений нормированных переменными х1* и х2* ортогональны столбцу из единиц матрицы модели, но не ортогональны между собой х1*Тх2*=2,408≠0. Оценка параметров модели (6.5.11) выполняется также методом наименьших квадратов по формуле
. При таком нормировании, как и для данных в левой части таблицы, столбцы значений нормированных переменными х1* и х2* ортогональны столбцу из единиц матрицы модели, но не ортогональны между собой х1*Тх2*=2,408≠0. Оценка параметров модели (6.5.11) выполняется также методом наименьших квадратов по формуле  =(Х*ТХ*)–1Х*Туп* и оценки следующие:
=(Х*ТХ*)–1Х*Туп* и оценки следующие:  =0,818 и
=0,818 и 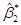 =–0,327. Для модели (6.5.11) также дисперсия sn2=1, поэтому матрица дисперсий и ковариаций вектора
=–0,327. Для модели (6.5.11) также дисперсия sn2=1, поэтому матрица дисперсий и ковариаций вектора  оценки параметров имеет вид (Х*ТХ*)–1=
оценки параметров имеет вид (Х*ТХ*)–1= .
.
Из полученной матрицы видно, что оценки параметров b1 и b2 коррелированы и, в действительности, нельзя рассматривать разности β1*– и β2*–
и β2*–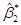 в качестве случайных переменных, имеющих распределение хи-квадрат. Однако с целью сравнения результатов эксперимента, выполненного по плану, где все столбцы матрицы модели ортогональны, и по плану, где это условие не соблюдается, допустим, что они имеют распределение хи-квадрат. Тогда, зная значения
в качестве случайных переменных, имеющих распределение хи-квадрат. Однако с целью сравнения результатов эксперимента, выполненного по плану, где все столбцы матрицы модели ортогональны, и по плану, где это условие не соблюдается, допустим, что они имеют распределение хи-квадрат. Тогда, зная значения  =0,818 и
=0,818 и 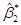 =–0,327 и решая уравнения
=–0,327 и решая уравнения
(β1*– )2/0,392=3,841 и (β2*–
)2/0,392=3,841 и (β2*–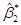 )2/0,392=3,841 (6.5.12)
)2/0,392=3,841 (6.5.12)
относительно β1* и β2*, можно найти индивидуальные доверительные интервалы для этих параметров. Для данных таблицы 6.5.1 с не ортогональными столбцами х1* и х2* они получаются следующие: для β1* доверительный интервал 0,818±1,227 длиной 2,454 и для β2* доверительный интервал –0,327±1,227 тоже длиной 2,454.
Совместную доверительную область параметров b1* и b2* будем искать тоже по аналогии с выражениями (6.5.9) и (6.5.10). При этом, как предложено в [Box, Draper (2007) стр.67], используя матрицу Х*ТХ*= , добавим в левой части выражения (6.5.10) удвоенную ковариацию переменных β1*–
, добавим в левой части выражения (6.5.10) удвоенную ковариацию переменных β1*– и β2*–
и β2*–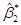
4(β1*– )2+4(β2*–
)2+4(β2*–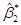 )2+4,816(β1*–
)2+4,816(β1*– )(β2*–
)(β2*–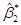 )≤5.991 (6.5.13)
)≤5.991 (6.5.13)
Следовательно, круговая совместная 95% доверительная область параметров b1* и b2* с центром в точке с координатами ( ,
,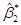 ) определяется неравенством
) определяется неравенством
4(β1*–0,818)2+4(β2*+0,327)2+4,816(β1*–0,818)(β2*+0,327)≤5.991 (6.5.14)
Эта совместная область и индивидуальные интервалы показаны на Рис.6.5.2.
На основании полученного результата, отметим, что ортогональный план на много более желателен, чем не ортогональный, в том смысле, что
Ø Площадь совместной доверительной области меньше,
Ø Длины индивидуальных доверительных интервалов меньше.
Вывод, следующий из сравнения дисперсионных матриц оценок, состоит в том, что более высокая точность оценок параметров получается при ортогональном плане. Однако чтобы делать такое сравнение должным образом для сравниваемых планов необходимо определять их масштаб в одинаковых единицах. При данном сравнении это соблюдалось посредством равенства числу 4 сумм квадратов нормированных элементов каждого столбца для обоих планов.
Теперь рассмотрим Рис.6.5.1 и Рис. 6.5.2 вместе. Во-первых, сравним доверительные интервалы и совместную доверительную область на Рис. 6.5.2 для не ортогонального плана. Рассмотрим пару значений (β10, β20) параметров, соответствующих координатам точки «Р». Видно, что хотя β10 имеет место в пределах доверительного интервала для β1 и β20 имеет место в пределах доверительного интервала для β2, сама точка с координатами (β10, β20) попадает за пределы совместной области. Это значит, что хотя значение β10 и допустимо для некоторых значений параметра β2, но оно недопустимо для конкретного значения β20. В общем случае, чтобы понять совместную приемлемость значений группы параметров необходимо рассматривать совместную область и совсем непросто сделать это видимым, когда имеется более двух или трёх параметров. На Рис.6.5.1 показано как с использованием ортогонального плана это затруднение значительно уменьшается, но не устраняется. Ортогональные планы приводят к круговым контурам для двух параметров или гипер-сферическим контурам для большего числа параметров.
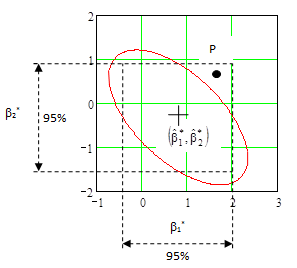
Рис.6.5.2. 95% совместная доверительная область и доверительные интервалы не ортогонального плана эксперимента
Упражнения
6.1. При испытаниях полупроводниковых устройств памяти получены приведенные ниже данные
| Напряжение питания при операции «запись», x | 25,00 | 25,05 | 25,10 | 25,15 | 25,20 |
| Время хранения (час х10–4), у | 1,55 | 2,36 | 3,93 | 7,11 | 13,52 |
- Найдите оценки параметров модели у=b0+b1x +e, а также оценки ожидаемых значений переменной у и остатки. Подтвердите, что
![]() =
=![]() +
+![]() с погрешностью ошибки округления.
с погрешностью ошибки округления. - Пронормируйте переменную x по формуле x=(x–x0)/S. Какие значения имеют x0 и S.
- Найдите оценки параметров модели у=b0+b1x+e, а также оценки ожидаемых значений переменной (у) и остатки.
- Какая из моделей у=b0+b1x +e и у=b0+b1x+e является предпочтительной? Почему?
- Что показывают остатки?
- Предлагается провести анализ не с самой переменной (у), а с преобразованной переменной w=log(y). Найдите оценки параметров модели w=b0+b1x+e.
- Для модели w=b0+b1x+e проверьте гипотезу (b0, b1)=(0,6; 0,25). Каковы выводы?
6.2. В предыдущем упражнении можно подумать, что было бы лучше апроксимировать имеющиеся данные моделью у=b0+b1x+b2x2+e. Сделайте анализ. Вы согласны? Объясните.
6.3. Рассмотрим модель у=bх+e, где значения переменной х элементы вектора хT=[1, 1, 1, 1, 1], а соответствующие значения переменной (у) элементы вектора уT=[11, 8, 9, 10, 7]. Оцените параметр b и проверьте гипотезу H0: b=8 в сравнении с H1: b≠8.
6.4. (Источник: Bain W.A., Batty J.E. Inactivation of adrenaline and nonadrenaline by human and other mammalian liver in vitro, British Journal of Pharmacology and Chemotherapy, 11, 1956, 52-57) Данные в приведённой ниже таблице представляют п=14 концентраций адреналина, переменная у (эрг/мл), для пяти «периодов в нижних тканях», переменная x (мин), нормированная в х.
| x (мин) | х | у (эрг/мл) | Sy | ||
| 6 | –2 | 30,0 | 28,6 | 28,5 | 87,1 |
| 18 | –1 | 8,9 | 8,0 | 10,8 | 27,7 |
| 30 | 0 | 4,1 | - | 4,7 | 8,8 |
| 42 | 1 | 1,8 | 2,6 | 2,2 | 6,6 |
| 54 | 2 | 0,8 | 0,6 | 1,0 | 2,4 |
| 132,6 |
- Как выполнено нормирование?
- Допустим, что данные представляют 14 независимых наблюдений. Оцените параметры модели у=b0+b1x+e и покажите, что она неадекватная. Какую другую модель вы рекомендуете?
- Оцените параметры другой модели.
- Теперь, обратившись к статье, находим, что столбцы значений переменной (у) в таблице являются отдельными опытами, в каждом из которых образцы брались последовательно во времени из той же пробирки. Может это повлиять на анализ? Если да, то, как и почему?
6.5. Для постулируемой модели у=b0+b1x+e, методом наименьших квадратов находятся оценки параметров для значений х1, х2, ..., хп переменной х. Первые три момента переменной х находятся по формулам:
 =
= /п, с=
/п, с= /п, d=
/п, d= /п,
/п,
где i=1, 2, ..., п. Покажите, что, если модель у=b0+b1x+b11x2+e вызывает опасение и используется модель у=b0+b1x+e, то
Лекция "11 Несобственные кратные интегралы" также может быть Вам полезна.
Е(b0)=b0+[(c– d)(c–
d)(c– )]b11
)]b11
Е(b1)=b1+[(d– c)(c–
c)(c– )]b11.
)]b11.
- Возможно ли выбрать такой набор значений х1, х2, ..., хп, что обе оценки будут несмещёнными? Объясните.
- Возможно ли выбрать такой набор значений х1, х2, ..., хп, что оценка b1 будут несмещённой? Если да, то предложите простой способ достижения этого.
6.6. Покажите, что статистика t1= в (6.3.12) имеет нецентральное распределение t(n–2, d) с параметром d=
в (6.3.12) имеет нецентральное распределение t(n–2, d) с параметром d= .
.
6.7. Сделайте проверку гипотезы H0: b1=с в сравнении с H1: b1≠с.
6.8. (а) Сделайте проверку гипотезы H0: b0=а в сравнении с H1: b0≠а.
(б) Найдите доверительный интервал для b0.


 =
= +
+ с погрешностью ошибки округления.
с погрешностью ошибки округления.



















