Проверка статистических гипотез о параметрах модели
6.3. Проверка статистических гипотез о параметрах модели
В статистическом линейном моделировании при анализе модели требуются определённые проверки гипотез о её параметрах. В этом разделе представлены несколько важных методов проверки гипотез. Для этих методов необходимо соблюдение сделанных в разделе 6.1 допущений.
Для проверки гипотез необходим вектор оценки ожидаемых значений переменных отклика в опытах эксперимента. Он вычисляется по формуле
 ≡
≡ =X
=X . (6.3.1)
. (6.3.1)
Разность между вектором получаемых в опытах эксперимента значений переменных отклика и вектором оценки их ожидаемых значений получается в виде
y– =y–X
=y–X =y–X(XТX)–1XТy
=y–X(XТX)–1XТy
=[I–X(XТX)–1XТ]y (6.3.2)
и называется вектором остатков или остаточных ошибок. Сумму SE квадратов остатков можно записать с использованием вектора y– остатков в векторной форме
остатков в векторной форме
SE= =(y–
=(y– )Т(y–
)Т(y– ). (6.3.3)
). (6.3.3)
Рекомендуемые материалы
Формула расчёта суммы SE получается подстановкой выражения (6.3.2) вектора y– остатков в (6.3.3). Учитывая, что матрица I–X(XТX)–1XТ симметричная и идемпотентная, а произведение [I–X(XТX)–1XТ]X=О, то в результате имеем
остатков в (6.3.3). Учитывая, что матрица I–X(XТX)–1XТ симметричная и идемпотентная, а произведение [I–X(XТX)–1XТ]X=О, то в результате имеем
SE=yТ[I–X(XТX)–1XТ]y (6.3.4)
=yТy–yТX(XТX)–1XТy
=yТy– XТy, (6.3.5)
XТy, (6.3.5)
так как  =yТX(XТX)–1. Эта формула удобна для расчёта суммы SE. В ней yТy – сумма квадратов получаемых в опытах значений переменных отклика и
=yТX(XТX)–1. Эта формула удобна для расчёта суммы SE. В ней yТy – сумма квадратов получаемых в опытах значений переменных отклика и  XТy – сумма произведений элементов вектора
XТy – сумма произведений элементов вектора  на соответствующие элементы вектора XТy, являющегося правой частью нормальных уравнений XТXq=XТy метода наименьших квадратов. При этом заметим, что при таком описании выражения (6.3.5) вектор XТy должен быть в точности таким какой он в нормальных уравнениях. Так, если при решении уравнений XТXq=XТy некоторые или все уравнения изменяются путём сокращения общих членов, то в члене
на соответствующие элементы вектора XТy, являющегося правой частью нормальных уравнений XТXq=XТy метода наименьших квадратов. При этом заметим, что при таком описании выражения (6.3.5) вектор XТy должен быть в точности таким какой он в нормальных уравнениях. Так, если при решении уравнений XТXq=XТy некоторые или все уравнения изменяются путём сокращения общих членов, то в члене  XТy выражения (6.3.5) используется не изменённый, а исходный вектор XТy нормальных уравнений.
XТy выражения (6.3.5) используется не изменённый, а исходный вектор XТy нормальных уравнений.
Разделение суммы квадратов переменных отклика
Сумма ST квадратов значений переменных отклика находится по формуле
ST= =yТy
=yТy
и сумма квадратов разностей значений переменных отклика и их оцениваемых ожидаемых значений определяется по формуле SE=yТy– XТy. Разность между ними
XТy. Разность между ними
SR=ST–SE=yТy–yТy+ XТy=
XТy= XТy
XТy
представляет часть суммы ST получаемой в результате выполнения регрессии и поэтому называемой регрессионной суммой квадратов. Это разделение суммы ST в виде
SR= XТy(=
XТy(= XТX
XТX ) (6.3.6)
) (6.3.6)
SE=yТy– XТy
XТy
--------------------
ST=yТy
может быть сведено в таблицу дисперсионного анализа.
Разделяя матрицу X на столбцы в виде X=[1, x], выражение для суммы SE можно записать так
SE=yТy–[ ,
, 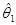 ]
]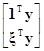
=yТy–[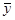 –
–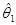
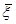 ,
, 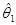 ]
]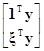 [в силу (6.2.4)]
[в силу (6.2.4)]
=yТy–n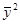 –
–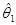 ( xТy–n
( xТy–n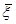
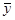 )
)
=STс–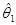 xскТy,
xскТy,
где STс=yТy–n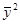 обозначает скорректированную усреднённым
обозначает скорректированную усреднённым 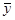 сумму квадратов значений переменных отклика, а произведение xскТy=xТy–n
сумму квадратов значений переменных отклика, а произведение xскТy=xТy–n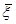
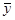 обозначает скорректированное усреднёнными
обозначает скорректированное усреднёнными 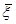 и
и 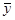 произведение xТy. В этом случае разность ST–SE принимает вид
произведение xТy. В этом случае разность ST–SE принимает вид
SR=ST–SE=n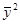 +
+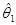 xскТy.
xскТy.
Это разделение суммы ST может быть выполнено также в виде
SR=n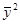 +
+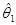 xскТy
xскТy
SE=yТy–n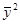 –
–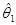 xскТy
xскТy
--------------------
ST=yТy
и сведено в таблицу дисперсионного анализа.
Теперь допустим, что уравнение модели не содержит переменную x и имеет вид уi=q0+ei. В этом случае оценкой  параметра q0 является усреднённое
параметра q0 является усреднённое 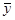 и регрессионная сумма квадратов равна n
и регрессионная сумма квадратов равна n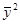 . Её можно считать корректировкой усреднённым
. Её можно считать корректировкой усреднённым 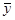 и записать как SМ=n
и записать как SМ=n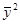 . Тогда сумму SR можно представить в виде SR=SМ+
. Тогда сумму SR можно представить в виде SR=SМ+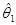 xскТy и вычитанием SМ получить скорректированную усреднённым регрессионную сумму квадратов
xскТy и вычитанием SМ получить скорректированную усреднённым регрессионную сумму квадратов
SRс=SR–SМ=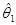 xскТy.
xскТy.
С учётом этого, разделение суммы ST может быть выполнено в виде
SМ=n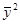 (6.3.7)
(6.3.7)
SRс=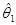 xскТy
xскТy
SE=yТy–n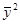 –
–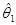 xскТy
xскТy
--------------------
ST=yТy
и сведено в таблицу дисперсионного анализа.
Также можно получить и скорректированную усреднённым значением 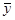 сумму квадратов значений переменных отклика по формуле
сумму квадратов значений переменных отклика по формуле
STс=ST–SМ=yТy–n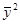
Её можно разделить в виде
SRс=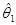 xскТy (6.3.8)
xскТy (6.3.8)
SE=yТy–n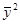 –
–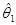 xскТy
xскТy
--------------------
STс=yТy–n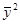
и на основании этого получить таблицу дисперсионного анализа.
Распределения сумм квадратов
Вместе с допущениями раздела 6.1 будем теперь ещё считать, что случайные переменные ei в модели (6.1.1) распределены по нормальному закону. Вектор e этих переменных имеем распределение N(0, s2I). На основе этого получаются параметры распределений вектора у и его функций. Так, записывая модель (6.1.1) в матричном виде у=Xq+e, имеем e=у–Xq и, следовательно, у~N(Xq, s2I).
Вектор оценки параметров модели находится по формуле  =(XТX)–1XТy и сумма квадратов остатков, в силу (6.3.4), записывается в виде
=(XТX)–1XТy и сумма квадратов остатков, в силу (6.3.4), записывается в виде
SE=yТ[I–X(XТX)–1XТ]y.
Произведения матриц (XТX)–1XТ[I–X(XТX)–1XТ]=О, поэтому по следствию 1 теоремы 5.6.1 вектор оценки  параметров модели и находимая по формуле (6.2.16) оценка s2 дисперсии распределены независимо.
параметров модели и находимая по формуле (6.2.16) оценка s2 дисперсии распределены независимо.
Сумма квадратов остатков SЕ=yТ[I–X(XТX)–1XТ]y является квадратичной формой относительно вектора у. Матрица этой квадратичной формы идемпотентная и имеет ранг[I–X(XТX)–1XТ]=п–р. По второму и третьему допущениям раздела 6.1 дисперсия D(y)=s2I. Тогда по следствию 2 теоремы 5.5 квадратичная форма yТ(I–X(XТX)–1XТ)y/s2 имеет нецентральное распределение c2{п–р, (Xq)T[I–X(XТX)–1XТ]Xq/(2s2)}. В нём параметр не центральности обращается в нуль
(Xq)T(I–X(XТX)–1XТ)Xq=qTXT(I–X(XТX)–1XТ)Xq=qT(XTX–XTX)q=0.
Следовательно, величина SЕ/s2 имеет центральное распределение c2(п–р).
Зная, что SЕ/s2 имеет центральное распределение c2(п–р), покажем, что суммы SR, SМ и SRс имеют нецентральные распределения c2. Более того, они распределены независимо от SЕ. На основании этого могут быть получены статистики, имеющие нецентральные распределения F. При определённых нулевых гипотезах эти статистики приобретают центральные распределения F и на основе этого позволяют проверить рассматриваемые нулевые гипотезы.
Сумма SR= XТy=yТX(XТX)–1XТy является квадратичной формой относительно вектора у. Её матрица XТ(XТX)–1XТ идемпотентная и произведения этой матрицы с матрицей I–X(XТX)–1XТ дают нулевую матрицу. Следовательно, по следствию 1 теоремы 5.6.2 квадратичные формы SR и SЕ распределены независимо, а по следствию 2 теоремы 5.5 величина SR/s2 имеет нецентральное распределение хи-квадрат
XТy=yТX(XТX)–1XТy является квадратичной формой относительно вектора у. Её матрица XТ(XТX)–1XТ идемпотентная и произведения этой матрицы с матрицей I–X(XТX)–1XТ дают нулевую матрицу. Следовательно, по следствию 1 теоремы 5.6.2 квадратичные формы SR и SЕ распределены независимо, а по следствию 2 теоремы 5.5 величина SR/s2 имеет нецентральное распределение хи-квадрат
SR/s2~c2{ранг[X(XТX)–1XТ], (Xq)TX(XТX)–1XТXq/(2s2)},
то есть,
SR/s2~c2[р, qTXТXq/(2s2)],
где ранг[X(XТX)–1XТ]=р.
В силу (6.3.7), так же имеем SМ=n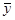 2=yТ11Тy/n, где матрица 11Т/n идемпотентная и её произведения с матрицей I–X(XТX)–1XТ дают нулевую матрицу. Следовательно, квадратичная форма SМ распределена независимо от SЕ, а величина SМ/s2 имеет нецентральное распределение c2[ранг(11Т/n), (Xq)T11Т/nXq/(2s2)], то есть,
2=yТ11Тy/n, где матрица 11Т/n идемпотентная и её произведения с матрицей I–X(XТX)–1XТ дают нулевую матрицу. Следовательно, квадратичная форма SМ распределена независимо от SЕ, а величина SМ/s2 имеет нецентральное распределение c2[ранг(11Т/n), (Xq)T11Т/nXq/(2s2)], то есть,
SM/s2~c2[1, qTXТ11ТXq/(2ns2)],
где ранг(11Т/n)=1.
Кроме того, как показано выше, SRс=SR–SМ, следовательно эту сумму можно записать в виде квадратичной формы
SRс=yТX(XТX)–1XТy–yТ11Тy/n
=yТ[X(XТX)–1XТ–11Т/n)y.
Матрица этой квадратичной формы симметричная и идемпотентная
[X(XТX)–1XТ–11Т/n]2=X(XТX)–1XТ–11ТX(XТX)–1XТ/n–X(XТX)–1XТ11Т/n+11Т/n11Т/n
=X(XТX)–1XТ–11Т/n,
где 11ТX(XТX)–1XТ=11Т и X(XТX)–1XТ11Т=11Т. Это получается на основании равенства XТX(XТX)–1XТ=XТ, так как первый столбец матрицы X состоит из единиц [см. Searle (1971) cтр.95 и раздел 8.4 этой книги]. Эта матрица имеет ранг[X(XТX)–1XТ–11Т/n]=р–1. Произведения её с матрицами I–X(XТX)–1XТ и 11Т/n дают нулевые матрицы. Поэтому квадратичная форма SRс распределена независимо от SЕ и SM, а величина SRс/s2 имеет нецентральное распределение хи-кадрат
SRс/s2~c2{р–1, qTXT[X(XТX)–1XТ–11Т/n]Xq/(2s2)}
~c2[р–1, qT(XTX–XT11ТX/n)q/(2s2)].
Статистики с распределением F для проверки гипотез
Используя данное в разделе 5.4 определение нецентрального распределения F, можно получить статистику FR по формуле
FR= .
.
В правой части формулы числитель представляет выражение оценки дисперсии, которая объясняется регрессионной моделью, а знаменатель представляет выражение оценки дисперсии, которая не объясняется регрессионной моделью. Отношение объяснённой и необъяснённой дисперсий даёт другой критерий рассмотрения регрессионной линейной модели. Проверка по этому критерию позволяет решить, приемлема ли постулируемая линейная модель для описания имеющихся данных эксперимента.
Статистика FR имеет нецентральное распределение F
FR ~F[р, n–р, qTXТXq/(2s2)]. (6.3.9)
Вместе с этим, статистика FМ рассчитывается по формуле
FМ=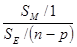
и эта статистика тоже имеет нецентральное распределение F
FМ ~F[1, n–р, qTXТ11ТXq/(2ns2)]. (6.3.10)
Статистика FRс вычисляется по формуле
FRс=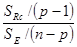
и имеет также нецентральное распределение F
FRc~F[р–1, п–р, qT[XTX–XT11ТX/n]q/(2s2)].
Параметр не центральности этого распределения можно преобразовать. Если использовать разделение матрицы X=[1, x], где x - вектор столбец значений переменной x, а вектора q= , то после соответствующих преобразований числитель параметра не центральности можно представить в виде
, то после соответствующих преобразований числитель параметра не центральности можно представить в виде
qT[XTX–XT11ТX/n]q=q1(xТx–xТ11Т/nx)q1.
Таким образом, распределение статистики FRc записывается так
FRc~F[р–1, п–р, q1(xТx–xТ11Т/nx)q1/(2s2)]. (6.3.11)
Вычисления статистик с распределениями F сводятся в таблицы дисперсионного анализа. Например, вычисление статистики FR сведено в таблицу 6.3.1. В этой таблице приведены не только суммы квадратов, но и степени свободы соответствующих распределений хи-квадрат. В столбце средних квадратичных величин показан расчёт числителя и знаменателя статистики FR. А в крайнем правом столбце показана формула расчёта самой статистики FR. Таким образом, таблица дисперсионного анализа является просто удобной формой представления этапов расчёта статистики FR.
Таблица 6.3.1. Дисперсионный анализ значимости регрессии
| Источники вариаций | Суммы квадратов | Степени свободы | Средние квадратичные | Статистика проверки FR |
| Регрессия | SR= | р | SR/р |
|
| Остатки | SE=yТy– | n–р | SE/(n–р) | |
| Итого | ST=yТy | n |
Расчёт статистик FМ и FRс представлен в таблице 6.3.2. Она содержит больше информации, чем таблица 6.3.1. Таблица 6.3.2 показывает разделение суммы квадратов SR на SМ и SRс.
Таблица 6.3.2. Дисперсионный анализ с учётом влияния усреднённого 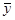
| Источники вариаций | Суммы квадратов | Степени свободы | Средние квадратичные | Статистики проверки |
| Усреднённое | SМ=n | 1 | SМ/1 | FМ= |
| Регрессия | SRс=yТX(XТX)–1XТy–yТ11Тy/n | р–1 | SRс/(р–1) | FRс= |
| Остатки | SE=yТy– | n–р | SE/(n–р) | |
| Итого | ST=yТy | n |
Проверка гипотез по статистикам с распределением F
При определённых нулевых гипотезах параметры не центральности, представленных выражениями (6.3.9) - (6.3.11) распределений F, обращаются в нуль. Поэтому эти нецентральные распределения становятся центральными и, следовательно, вычисленные в таблицах 6.3.1 и 6.3.2 статистики могут использоваться для проверки нулевых гипотез.
С помощью статистики FR можно проверить статистическую гипотезу о значимости регрессии, то есть, проверить соответствует ли постулируемая линейная модель данным эксперимента. Для этого рассматриваются нулевая гипотеза H0: q=0 и альтернативная гипотеза H1: q≠0. Если нулевая гипотеза H0: q=0 верна, то в выражении (6.3.9) параметр не центральности распределения статистики FR становится равным нулю и эта статистика приобретает центральное распределение F(р, п–р). Её расчётное значение может быть сравнено с критическим значением Fкр случайной переменной, имеющей центральное распределение F(р, п–р) и интегральную вероятность равную 1–α на интервале от 0 до Fкр. Если, при выбираемой обычно вероятности 1–a=0,95, значение статистики FR больше значения Fкр, то нулевая гипотеза H0: q=0 ложна, а если нет, то верна. Критические значения Fкр находятся по таблицам распределения F [Searle (1971) стр.526; Box, Draper (2007) стр.752] или с использованием специальных компьютерных программ.
Относительно постулируемой функции Е(у)=Xq модели можно тогда сказать, что когда статистика FR имеет значимую величину и существует соответствие между данными эксперимента и постулируемой моделью, то модель описывает значительную часть изменений переменных отклика. Но это не значит, что для выбранной переменной x эта модель обязательно наилучшая. Могут быть другие влияющие на отклик переменные, c помощью которых достигается лучшее описание изменений переменных отклика, или может быть нелинейная функция переменной x, которая не хуже описывает изменения переменных отклика, чем линейная функция переменной x. Все эти дополнительные обстоятельства совместимы со значимой величиной статистики FR и следующим выводом, что данные соответствуют модели с функцией Е(у)=Xq.
В выражении (6.3.10) параметром не центральности распределения статистики FМ является qTXТ11ТXq/(2ns2)=(1ТXq)2/(2ns2). В числителе этого выражения произведение можно представить в виде 1ТXq=1ТЕ(у)=Е(1Ту)=Е(n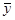 )=nЕ(
)=nЕ(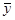 ). Следовательно параметр не центральности распределения статистики FМ становится равным n[Е(
). Следовательно параметр не центральности распределения статистики FМ становится равным n[Е(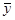 )]2/(2s2). Он принимает нулевое значение, если гипотеза H0: Е(
)]2/(2s2). Он принимает нулевое значение, если гипотеза H0: Е(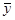 )=0 верна. Таким образом, статисту FМ можно использовать для проверки гипотезы, что ожидаемое значение усреднённого переменных отклика является нулевым. Это является объяснением выражения проверки среднего, которое иногда используется для описания основанной на статистике FМ проверки.
)=0 верна. Таким образом, статисту FМ можно использовать для проверки гипотезы, что ожидаемое значение усреднённого переменных отклика является нулевым. Это является объяснением выражения проверки среднего, которое иногда используется для описания основанной на статистике FМ проверки.
Другое рассмотрение проверки по статистике FМ основывается на функции Е(уi)=q0 модели уi=q0+ei. Регрессионной суммой квадратов этой модели является SМ и параметр не центральности в выражении (6.3.10) равен пq02/(2s2). Следовательно, статистику FМ можно использовать для проверки описывает ли модель уi=q0+ei изменения переменных отклика.
При использовании статистики FR проверяется гипотеза, что оба параметра q0 и q1 модели одновременно равны нулю. Однако проверка нулевой гипотезы H0: q1=0, что только параметр q1 переменной x равен нулю, основывается на статистике FRс таблицы 6.3.2. Это получается потому, что в выражении (6.3.11) распределения статистики FRс параметр не центральности равен нулю, если верна нулевая гипотеза H0: q1=0. В этом случае статистика FRс приобретает центральное распределение F со степенями свободы р–1 и п–р. Таким образом, статистика FRс даёт возможность проверить гипотезу H0: q1=0. Если расчётная величина статистики FRс оказывается равной или больше критического значения имеющей распределение F(р–1, п–р) случайной переменной при выбираемой вероятности 1–a, то нулевая гипотеза H0: q1=0 ложна. При этом если сначала расчёт статистики FМ показал, что гипотеза H0: Е(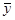 )=0 ложна, а затем расчёт статистики FRс показал, что гипотеза H0: q1=0 ложна, то получается, что модель с переменной x объясняет значительно лучше изменения переменных отклика, чем модель уi=q0+ei.
)=0 ложна, а затем расчёт статистики FRс показал, что гипотеза H0: q1=0 ложна, то получается, что модель с переменной x объясняет значительно лучше изменения переменных отклика, чем модель уi=q0+ei.
Проверки с использованием статистик FМ и FRс основаны на суммах квадратов SМ и SRс которые, как показано выше, распределены независимо. Они находятся в числителях формул расчёта статистик FМ и FRс. Поэтому значимость или незначимость этих статистик статистически независимы друг от друга по числителям их расчётных формул. Однако сами распределения статистик FМ и FRс не являются статистически независимы, так как в знаменателе их формул находится одна и та же сумма SE. Поэтому рассмотрение уровней значимости обеих статистик FМ и FRс представляет случай совместного статистического вывода, что выходит за рамки этой книги. Желающим познакомиться с этим подробно рекомендуется книга [Miller (1981)]. Однако в дальнейшем значимость статистик FМ и FRс будет обсуждаться, игнорируя существующую проблему совместного статистического вывода.
Выше обсуждался случай когда обе статистики FМ и FRс значимы. Но в практике может встретиться случай когда статистика FМ незначима, а статистика FRс значима. Это означает, что даже, если Е(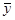 ) было бы нулевым, то использование переменной x давало бы возможность модели объяснять изменения переменных отклика. Так происходит тогда, когда в опытах эксперимента переменные отклика принимают положительные и отрицательные значения.
) было бы нулевым, то использование переменной x давало бы возможность модели объяснять изменения переменных отклика. Так происходит тогда, когда в опытах эксперимента переменные отклика принимают положительные и отрицательные значения.
Пример 6.3.1. Используя данные таблицы 6.2.1, проведём дисперсионный анализ модели получаемой при моделировании зависимости коэффициента усиления транзистора от эмиттерной дозы из примера 6.2.1. Таблица 6.3.2 представляет дисперсионный анализ наиболее полно, поэтому на её основе результаты расчётов представим в таблице 6.3.3.
Таблица 6.3.3. Дисперсионный анализ модели из примера 6.2.1.
| Источники вариаций | Суммы квадратов | Степени свободы | Средние квадратичные | Статистики проверки |
| Усреднённое | SМ=1,7996х107 | 1 | 1,7996х107 | FМ=688,209 |
| Регрессия | SRс=2,8102х104 | 1 | 2,8102х104 | FRс=1,075 |
| Остатки | SE=2,0919х105 | 8 | 2,6149х104 | |
| Итого | ST=1,8234х107 | 10 |
Расчёт сумм квадратов выполнялся по представленным в таблице 6.3.2 формулам. При расчёте степеней свободы с использованием выражения ранг[X(XТX)–1XТ–11Т/n]=р–1 заметим, что для рассматриваемой модели ранг[X(XТX)–1XТ]=ранг(X)=р=2 и поэтому р–1 =1. Также в расчёте степеней свободы по формуле ранг[I–X(XТX)–1XТ]=п–р ранг матрицы I равен 10 и поэтому n–р=8.
Далее по найденным суммам квадратов и степеням свободы вычислялись средние квадратичные и сами статистики FМ и FRс. При выбранной вероятности 1–a=0,95 для этих статистик случайная величина с распределением F(1, 8) имеет критическое значение Fкр=5,318. Оно меньше FМ=688,209, но больше FRс=1,075. Следовательно, гипотеза H0: Е(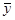 )=0 ложна, а гипотеза H0: q1=0 верна. Таким образом, в этом примере получен третий возможный случай когда статистика FМ значима, а статистика FRс незначима. Это указывает на то, что модель с переменной x не объясняет лучше изменения переменных отклика, чем модель с функцией Е(уi)=q0. Следовательно, представленные таблицей 6.2.1 результаты эксперимента описываются моделью уi=q0+ei.
)=0 ложна, а гипотеза H0: q1=0 верна. Таким образом, в этом примере получен третий возможный случай когда статистика FМ значима, а статистика FRс незначима. Это указывает на то, что модель с переменной x не объясняет лучше изменения переменных отклика, чем модель с функцией Е(уi)=q0. Следовательно, представленные таблицей 6.2.1 результаты эксперимента описываются моделью уi=q0+ei.
□
Проверка гипотез по статистикам с распределением t
Наряду со статистиками с распределением F для проверки гипотез относительно параметров модели могут использоваться статистики с распределением t [Rencher, Schaalje (2008) стр.132]. Как правило, гипотезы о параметре q1 имеют больший интерес, чем гипотезы о q0, так как основным часто является нахождение, существует ли линейная зависимость переменной (у) отклика от переменной x. Поэтому проверяется гипотеза H0: q1=0, которая утверждает, что модель уi=q0+q1xi+ei не объясняет линейную зависимость (у) от x.
При проверке гипотезы H0: q1=0 полагают, что переменные уi отклика распределены по нормальному закону N(q0+q1xi, s2). Тогда оценки 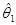 и s2 имеют следующие свойства:
и s2 имеют следующие свойства:
1. Оценка 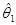 имеет нормальное распределение N[q1, s2/
имеет нормальное распределение N[q1, s2/ ].
].
2. Величина (n–2)s2/s2 имеет распределение c2(n–2).
3. Оценки 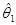 и s2 распределены независимо.
и s2 распределены независимо.
Из этих трех свойств и, в силу (5.4.8), следует, что статистика
Лекция "Иван IV Грозный и политика опричнины" также может быть Вам полезна.
t1= (6.3.12)
(6.3.12)
имеет нецентральное распределение t(n–2, d) с параметром не центральности δ. Этот параметр задается выражением δ=Е(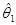 )/
)/ =q1/[s/
=q1/[s/ ] и, если q1=0, то в силу (5.4.6), статистика t1 принимает центральное распределение t(n–2).
] и, если q1=0, то в силу (5.4.6), статистика t1 принимает центральное распределение t(n–2).
При двусторонней альтернативной гипотезе H1: q1≠0, гипотеза H0: q1=0 ложна, если |t1|>tα/2(n–2), где tα/2(n–2) - верхнее α/2 процентное значение центрального распределения t и α - желаемый уровень значимости проверки (то есть, вероятность отклонить гипотезу H0, когда она верна).
Пример 6.3.2. Проверим гипотезу H0: q1=0 на основе статистики t1 с использованием полученных в примерах 6.2.1 и 6.2.2 величин 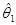 =–197,6 и s=161,7 оценки. В силу (6.3.12), статистика t1 вычисляется так
=–197,6 и s=161,7 оценки. В силу (6.3.12), статистика t1 вычисляется так
t1= =
= =–0,879.
=–0,879.
Так как |t1|=0,879<t0,95(8)=1,860, то гипотеза H0: q1=0 верна. Этим ещё раз подтверждает результат, полученный в примере 6.3.1.