Линейные функции статистических моделей
2.6. Линейные функции статистических моделей
Наряду с функциями, получаемыми на основе теоретических рассмотрений, изучаемые зависимости могут быть описаны статистическими моделями с интерполирующими линейными функциями. В тех случаях, когда среднее отклика является непрерывной функцией влияющих на него переменных x0, x1, x2,..., xр–1, то возникает возможность его адекватного представления функцией линейной относительно параметров q0, q1,…, qр–1.
Случайная переменная отклика (у) имеет математическое ожидание Е(y). Оно может быть представлено линейной комбинацией факторов x0, x1,…, xp–1 в виде линейной функции
Е(y)=θ0x0+θ1x1+…+θр–1xр–1 (2.6.1)
линейной относительно параметров θ0, θ1,…, θр–1. Это ограничение линейностью не является столь значительным, как сначала может показаться. Например, многие функции отклика от нескольких факторов являются приблизительно линейными в достаточно малых областях значений этих факторов или их можно сделать линейными посредством соответствующего преобразования. Так, используя логарифмическое преобразование функции силы гравитации между двумя объектами, можно получить линейную функцию
log(F)=log(a )–b log(d). (2.6.2)
В данной книге считается, что случайная переменная отклика находится под действием влияющих на неё контролируемых и неконтролируемых факторов. Например, результат урожая может зависеть от количеств используемых азотных, калийных и фосфорных удобрений. Значения этих факторов устанавливаются экспериментатором, но результат урожая зависит и от неконтролируемых влияющих факторов, связанных, например, с погодой. Поэтому для учёта неустранимой вариации значений отклика и влияния на него неконтролируемых факторов к линейной комбинации влияющих факторов выражения (2.6.1) добавляется случайная переменная ε ошибки и статистическая линейная модель принимает вид
у=θ0x0+θ1x1+…+θр–1xр–1+ε. (2.6.3)
В статистике зависимость наблюдаемых значений случайной переменной отклика от выбранных влияющих на отклик переменных называется регрессией. Поэтому выражение (2.6.3) называют также линейной регрессионной моделью. В ней параметры θ0, θ1,…, θр–1 являются коэффициентами регрессии, а случайная переменная ε представляет случайные ошибки необъясняемые переменными x0, x1,…, xр–1.
Рекомендуемые материалы
Статистическим линейным моделям уделяется наибольшее внимание, как в теории, так и на практике. С теоретической точки зрения они легко поддаются математической обработке и в практических применениях большого разнообразия показали себя как имеющие огромное значение. В то время как требования к вычислениям для анализа таких моделей могут быть большими, они не являются непомерными и с использованием современных компьютеров такой анализ осуществим довольно легко.
Выражение (2.6.1) представляет функцию линейной модели. Оно не описывает полностью линейную модель (2.6.3). Эта модель содержит две случайные переменные (у) и ε чьи законы распределения ещё должны быть определены. А так как статистическая модель является чем-то гипотетическим, то её параметры θ0, θ1,…, θр–1 никогда не могут быть известны заранее и лучшее, что можно сделать, это их оценить. Оценка делается с использованием известных значений влияющих на отклик переменных и наблюдаемых значений переменной отклика. Обычно полагают, что данные отклика представляют случайную выборку из некоторой популяции его значений, к которой выражение (2.6.1) считается применимым. И для оценки параметров модели (2.6.3) используется метод наименьших квадратов.
В основе любой зависимости существует некоторый механизм, который если полностью понят, может быть представлен теоретической функцией [Box, Draper (2007) стр.1]. А если знать форму теоретической функции, не зная значений её параметров, то наилучшим является оценка этих параметры на основе экспериментальных данных. Этот подход используется в нелинейном регрессионном моделировании. Но метод нелинейной регрессии имеет математические трудности, которые на практике часто непреодолимы [Seber, Wild (2003) стр.vi]. Поэтому больше внимания уделяется методам статистического линейного моделирования.
Пусть моделируемая зависимость описывается истинной функцией среднего Е(y) отклика от переменных x0, x1,…, xр–1, включающей вектор θ физических постоянных. Форма этой функции неизвестна и, в общем, её можно представить в виде
Е(y)=f(x0, x1,…, xр–1, θ)=f(ξ, θ),
где ξT=[x0, x1,…, xр–1]. В ней неизвестны также и элементы вектора θ. В статистическом линейном моделировании функция f(ξ, θ) аппроксимируется линейной функцией g(ξ, β), которая ожидается, что может аппроксимировать ее локально.
Истинная функция аппроксимируется линейной функцией в виде f(ξ, θ)≈g(ξ, β). Таким образом линейная функция описывает приближенно зависимость ожидаемого отклика Е(y) от переменных ξ. В эксперименте для любого отдельного набора значений переменных ξ средняя величина Е(y) отклика неизвестна. Имеется только наблюдение y (или иногда некоторое число повторных наблюдений), подверженное ошибке ε=y–Е(y). И хотя в любом данном случае действительная ошибка ε неизвестна, полагается, что она из некоторого определенного распределения, называемого распределением ошибок. Далее положим, что ошибки с достаточным приближением распределены по нормальному закону и независимо одна от другой, имея одну и ту же дисперсию σ2. Тогда зависимость наблюдаемого значения у отклика от переменных вектора ξ описывается в две стадии. Зависимость y от Е(y) осуществляется через распределение ошибок и зависимость Е(y) от ξ описывается линейной функцией g(ξ, β) [Box, Draper (2007) стр. 213]
y <распределение ошибок> Е(y) <линейная функция> ξ.
Таким образом, существует два источника и два вида ошибок моделирования:
- Случайные ошибки, определяемые выражением ε=y–Е(y),
- Систематические ошибки Е(y)–g(ξ, β), возникающие из-за неспособности линейной функции g(ξ, β) точно аппроксимировать истинную функцию Е(y)=f(ξ, θ).
Важно иметь в виду, что в статистическом линейном моделировании присутствуют оба вида ошибок. Это рассмотрение полезно также в решении вопроса о том, как должна быть точна линейная функция. Поэтому в статистическом линейном моделировании возникает задача уменьшения уровня систематических ошибок, связанных с используемой линейной функцией g(ξ, β) отклика, много ниже уровня имеющихся случайных ошибок.
Полиномиальные функции линейных моделей
При описании зависимостей статистическими линейными моделями и построении самих моделей удобно иметь дело не с действительными цифровыми значениями влияющих на отклик переменных, а с нормированными или кодированными их значениями. Например, если на начальном этапе моделирования определено, что диапазоном изменения значений переменной ξj является ξj0±Sj, где ξj0 – основной уровень переменной, а Sj - интервал её варьирования, то удобно определить нормированную числовую переменную xi используя формулу [Box, Draper (2007) стр.17]
xj=(ξj–ξj0)/Sj. (2.6.4)
Так, если ξj - температура и рассматриваемый диапазон её значений определён в виде 115±10°, то для любого значения температуры имеется эквивалентное значение нормированной переменной xj=(ξj–115)/10. Заметим, что нормированные переменные являются просто удобными линейными преобразованиями исходных влияющих на отклик переменных. Следовательно, записанные в переменных xj выражения могут быть всегда легко переписаны в переменных ξj с использованием формулы (2.6.4).
Изучаемые зависимости могут описываться линейными моделями, функции которых имеют вид полиномов. В общем, полином в нормированных переменных х1, х2,…, хр является суммой членов, включающих сами переменные х1, х2,…, хр и их произведения. Член полинома имеет порядок l, если он представляется произведением l переменных х1, х2,…, хр (некоторые из которых могут повторяться). Например, такие члены полинома как х13, х1х22 и х1х2х3 все имеют порядок 3. Полином имеет порядок d, если содержит члены порядка d. Таким образом, если имеются две нормированные переменные х1 и х2, то в общем виде, для этих переменных полином может быть записан так
Е(y)=b0+(b1x1+b2x2)+(b11x12+b22x22+b12x1x2)
+(b111x13+b222x23+b112x12x2+b122x1x22)+(b1111x14+…)+..., (2.6.5)
где члены одного и того же порядка для удобства заключены в скобки. Заметим, что подстрочные обозначения коэффициентов полинома выбраны таким образом, чтобы каждый из них мог быть легко отнесён к соответствующему члену, включающему переменные х1, х2,…, хр. Например, b122 является коэффициентом для x1x2x2 или x1x22. В выражении (2.6.5) коэффициенты b являются (статистическими) параметрами, которые на практике должны оцениваться на основе экспериментальных данных. Из таблицы 2.6.1 видно, что число этих параметров быстро увеличивается с увеличением числа факторов и порядка полинома [Box, Draper (2007) стр.18].
Таблица 2.6.1. Число коэффициентов полиномов порядка d с р факторами
| Число факторов р | Порядок полинома d | |||
| 1 | 2 | 3 | 4 | |
| Число коэффициентов полиномов | ||||
| 2 | 3 | 6 | 10 | 15 |
| 3 | 4 | 10 | 20 | 35 |
| 4 | 5 | 15 | 35 | 70 |
| 5 | 6 | 21 | 56 | 126 |
Однако на практике часто можно предположить, что в ограниченной области изменения значений рассматриваемых факторов полиномы только первого или второго порядка могут использоваться для адекватного описания исследуемой зависимости.
Полином первого порядка
В выражении (2.6.5) первый набор в скобках включает члены первого порядка. Если отбросить все остальные члены, то исследуемая зависимость будет представлена линейной моделью с функцией в виде полинома первого порядка с двумя факторами x1 и x2
Е(y)=b0+b1x1+b2x2. (2.6.6)
Графически эта зависимость представляется некоторой наклонной плоскостью. Положение и наклон плоскости определяются коэффициентами b0, b1 и b2. В частности, как показано на Рис. 2.6.1(а), коэффициент b0 является точкой пересечения плоскости с осью Е(y) в начале осей x1 и x2 и коэффициенты b1 и b2 являются градиентами (наклонами) в направлениях осей x1 и x2. Сечения такой плоскости при разных значениях Е(y) представляются параллельными прямыми линиями. Некоторые из этих сечений плоскости на Рис. 2.6.1(а) спроецированы на плоскость (x1, x2) на Рис.2.6.1(b). Показанные на этих рисунках построения выполнены с использованием компьютерной программы Mathcad 13.
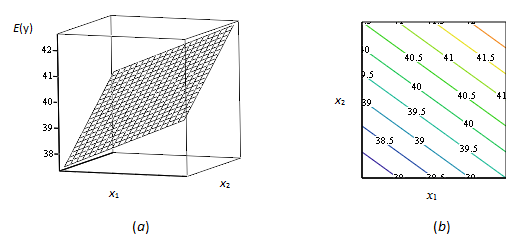
Рис. 2.6.1(а) Геометрическое представление полинома первого порядка (аппроксимация плоскостью) Е(y)=b0+b1x1+b2x2. (b) Контурная диаграмма с равноотстоящими сечениями плоскости, спроецированными на плоскость (x1, x2).
Полином второго порядка
Если в выражении (2.6.5) отбросить все члены после второго набора членов в скобках, то линейная модель изучаемой зависимости имеет функцию в виде полинома второго порядка с двумя факторами x1 и x2
Е(y)=b0+b1x1+b2x2+b11x12+b22x22+b12x1x2. (2.6.7)
Графически полином второго порядка изображается поверхностью второго порядка (или квадратичной) и, в данном случае, в зависимости только от двух факторов x1 и x2. На Рис.2.6.2 показано как посредством соответствующего выбора коэффициентов b функции второго порядка от переменных x1 и x2 могут принимать разные формы. Здесь графически показаны как сами функции, так и их контурные диаграммы.
Некоторый простой максимум показан на Рис.2.6.2 (а) и стационарный или плоский гребень показан на Рис. 2.6.2 (b). На Рис.2.6.2 (с) изображён поднимающийся гребень и на Рис.2.6.2 (d) показано то, что называют седлом или минимакс. И, несмотря на то, что даже локально нельзя с уверенностью ожидать, что исследуемая зависимость представляется такими функциями точно, тем не менее, основные свойства этой зависимости могут быть часто аппроксимированы одной из них.
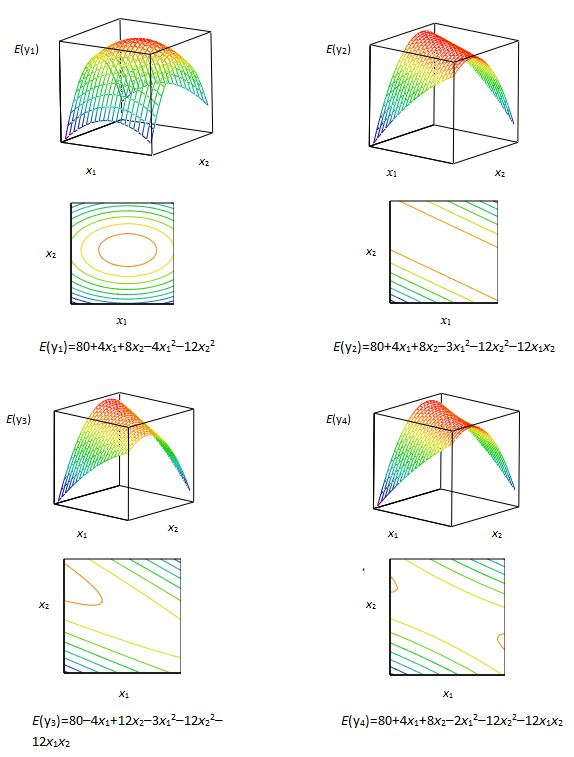
Рис. 2.6.2. Графические изображения функций отклика, определяемых полиномами второго порядка от двух факторов x1 и x2.
Модели с факторами в виде функций исходных переменных
Использование статистической линейной модели предполагает, что для исследуемой зависимости истинная функция отклика от влияющих на него переменных неизвестна и в ограниченной области изменения значений влияющих переменных эта функция может быть аппроксимирована простой полиномиальной функцией. Цель этой аппроксимации состоит в представлении истинной функции приближённо в локальной области значений используемых влияющих переменных. Такой аппроксимацией можно представить основные свойства истинной функции достаточно хорошо посредством полинома первого порядка. Эта аппроксимация далека от наилучшей, но она даёт правильное представление о характере воздействия влияющих на отклик переменных. Кроме этого, встречаемая неизбежно на практике статистическая ошибка может сделать сомнительной полезность дальнейшей разработки на этой стадии. Полиномом второго порядка можно снова только приблизительно представить истинную функцию локально. Существенное улучшение аппроксимации может быть часто достигнуто посредством преобразований отклика и влияющих на него переменных. После того как сделаны эти преобразования, то возможны существенно лучшие аппроксимации полиномами первого и второго порядка.
Таким образом, моделируемую зависимость можно описать линейной моделью с полиномиальной функцией. Хоть эта функция не содержит в себе никакой теории, но она может быть использована при прогнозировании значений отклика для заданных значений, влияющих на него переменных и, возможно, при определенных ограничениях. В случаях использования при моделировании планируемых экспериментов в представляющей интерес ограниченной области изменения значений факторов адекватное описание изучаемой зависимости может осуществляться с использованием соответствующей полиномиальной функции для каждого из п опытов эксперимента в виде
E(yi) =q0+ , (2.6.8)
, (2.6.8)
где q0, q1,…, qp–1 - параметры и i=1, 2,…, n.
В функциях статистических линейных моделей переменные z0, z1,…, zp–1 могут сами быть функциями исходных переменных ξ1, ξ2,…, ξk. Например, z1=sinξ1, z2=logξ2 и zp–1=ξ1ξ2. А когда z1=x1, z2=x2, z3=x12, z4=x22, z5=x1x2, то получается, что функция линейной модели представляет полиномиальную функцию второго порядка. Линейность таких функций обусловлена их линейностью относительно параметров, а не линейностью их переменных.
Для аппроксимации изучаемой зависимости линейными функциями обсуждаемыми способами были разработаны специальные планы экспериментов [Box, Wilson (1951); Box, Hunter (1957); Box, Draper (2007)] называемые планами функций отклика. План функции отклика порядка s специально разработан для оценки параметров полинома порядка s. Особое внимание уделялось планам первого и второго порядка. Полином второго порядка включает в себя все квадраты и взаимодействия исходных факторов x1, x2,..., xk. Эти члены полинома используются для моделирования нелинейной зависимости отклика от исследуемых факторов и их функций. А когда нелинейная зависимость монотонна относительно факторов в рассматриваемой области их значений, то можно использовать полиномиальную функцию первого порядка, в которой к факторам x1, x2,..., xk применяются преобразования возведения в степень [Box, Draper (1982)].
Использование фактора в виде теоретической функции
В качестве функции линейной модели наряду с использованием полиномиальных функций может использоваться и теоретическая функция исследуемой зависимости. Когда методы статистического моделирования с использованием планирования экспериментов применяются в физических и инженерных науках, где экспериментальная ошибка часто мала, то возможно и целесообразно искать более подробное и точное описание зависимости отклика от набора влияющих на него факторов.
Для изучаемой зависимости часто существует некоторая теоретическая функция ожидаемой величины отклика E(у) от переменных x1, x2,..., xk, включающая набор физических параметров (b1, b2,…, bu). Функция математического ожидания Е(у)=f(x1, x2,..., xk; b1, b2, …, bu) может быть получена теоретическим моделированием. Проверки адекватности таких функций и оценка их параметров обсуждались в работах [Box, Hunter (1962); Seber, Wild (2003)]. В этой книге рассматривается ситуация, когда имеющаяся теоретическая функция неадекватно представляет истинную неизвестную функцию исследуемой зависимости. Поэтому, с учётом имеющейся теоретической функции, истинная функция аппроксимируется приближённой полиномиальной функцией способной адекватно описать изучаемую зависимость в некоторой ограниченной области значений влияющих на отклик переменных x1, x2,..., xk.
В физических и технических науках можно использовать известные, лежащие в основе изучаемой зависимости, физические законы для аппроксимации истинной её функции посредством теоретической функции f(x1, x2,..., xq; b1, b2, …, bu). Эта функция может быть использована в статистическом моделировании вместо преобразований возведением в степень и произведений исходных влияющих переменных для описания нелинейной зависимости [Bokov (2007)]. В этом случае для нахождения полиномиальных функций отклика могут использоваться результаты экспериментов по планам первого порядка. Теоретическая функция может быть функцией всех или только подмножества рассматриваемых влияющих переменных x1, x2,..., xk, то есть q≤k. Эта функция может рассматриваться в качестве нелинейного преобразования переменных x1, x2,..., xq.
Рассмотренная ранее ситуация с полиномиальными функциями является такой, где каждая переменная z0, z1,…, zp–1 является функцией преобразования одной или нескольких исходных переменных x1, x2,..., xk. Но с помощью нелинейной теоретической функции получается более общее преобразование, которое даёт новую переменную z=f(x1, x2,..., xq; b1, b2, …, bu), являющуюся функцией ряда исходных переменных x1, x2,..., xq и включающую известные физические параметры b1, b2, …, bu. А если эта переменная умножается на параметр qz и получаемое произведение добавляется к правой части уравнения (2.6.8), то образуется новая линейная функция аппроксимации [Bokov (2010)]
E(yi)=q0+ +qzzi. (2.6.9)
+qzzi. (2.6.9)
Здесь математическое ожидание случайной переменной отклика представляется линейной комбинацией факторов z0, z1,…, zp–1, являющихся функциями исходных переменных x1, x2,..., xk, и основанного на доступной теории фактора z.
Связь между переменной (у) и её математическим ожиданием Е(у) осуществляется через распределение статистической ошибки, а связь между Е(у) и x1, x2,..., xk происходит через теоретическую нелинейную функцию f(x1, x2,..., xq; b1, b2, …, bu) и линейную функцию (2.6.9). При этом существуют два вида ошибок: случайные и систематические. Систематические ошибки возникают из-за неспособности сочетания теоретической и линейной функций точно описать истинную функцию изучаемой зависимость. На практике важно то, каким точным это сочетание должно быть.
Рекомендация для Вас - 2. Структура ЭВМ.
Методы представления изучаемых зависимостей аппроксимирующими функциями обсуждаемых видов называются методологией поверхностей (функций) отклика. В этой методологии важны принципы рандомизации, повторения и разбиения на блоки. На практике будут не только переменные, которые рассматриваются в настоящее время из таких источников знаний, как теория, мнения экспертов и эксперименты, но большее число N переменных, которые могут повлиять на отклик. И после применения адекватной рандомизации станет целесообразно применить модель
y=Zq+zqz+e, (2.6.10)
где y - вектор экспериментальных наблюдений отклика, Z - матрица линейной модели с первым столбцом из единиц, q - вектор параметров линейной модели, z - вектор значений фактора теории, получаемый вычислением функции f(x1, x2,..., xq; b1, b2, …, bu) для значений исходных влияющих переменных xi1, xi2,…, xiq, расположенных в строках матрицы X плана эксперимента, и qz - параметр фактора теории. Здесь для вектора e случайных ошибок можно допустить, что его элементы распределены независимо друг от друга и элементов Z и z.
Использование фактора теории в модели даёт конкретную иллюстрацию того, как знания в конкретной области могут повлиять на рассматриваемую проблему. В то время как метод факторного анализа часто превосходный инструмент для отбора факторов при отсутствии физических знаний, но когда такие знания имеются, то они должны быть включены в наибольшей мере в статистическое моделирование и анализ. Механическое использование факторных планов экспериментов неприемлемо, так как предполагает, что все воздействия являются линейными или, по крайней мере, аппроксимируются линейными функциями в пространстве значений используемых факторов. Рассмотрение физической природы моделируемой зависимости часто показывает, что она нелинейная. В то время как существует справедливый практический метод включать факторы низкого порядка в функцию модели, содержащую факторы высокого порядка, однако это не является обязательным. Даже в простых примерах физики отклики часто зависят от площадей и объёмов, в которых квадратичные и кубические члены должны оцениваться, даже если линейный член несущественный. Также, если отклик зависит от фактора по линейному дифференциальному уравнению и при известных граничных условиях, то уравнение регрессии является полиномом второго порядка без линейных воздействий.
Во многих случаях преобразования переменной отклика или факторов являются необходимыми – или из-за физических рассуждений, или математической пригодности или обоих. В этом случае, логарифмированием не только устраняются отрицательные значения времени, но возникает спор по решению моделировать время или скорость (или степени этого). Все эти рассуждения означают то, что реальные проблемы редко бывают скомпонованными и готовыми для анализа.
Любое обсуждение предложенного метода было бы неполным без нескольких предостережений. Этот метод хорошо подходит для использования в хорошо изученной области знаний (как например динамика жидкостей). Хотя многие прикладные проблемы дают исследователю похожие теоретические знания, но не все. В тех случаях, когда существует малое понимание проблемы, применимость этого подхода ограничена. Кроме этого, инженерные знания не могут и не должны заменять статистические методы. Скорее они должны дополнять их. Ни детерминированный инженерный подход, ни факторные статистические методы не приводят к удовлетворительным ответам. Только посредством объединения обоих достигается оптимальное решение. Однако для этого необходимы хорошие знания в области статистического линейного моделирования. Поэтому в главах 3-9 рассматриваются основы статистических линейных моделей с использованием матричной алгебры.




















