Сравнение дисперсий нормально распределённых данных
10.6. Сравнение дисперсий нормально распределённых данных
Иногда представляет интерес изучение степени вариации данных. В реальности этим может быть, например, вариация величины поглощения краски нейлоновой нитью или эффективность противотифозной вакцины. Уменьшающие дисперсию модификации изучаемого процесса могут представлять большую важность. И снова интересным может быть сравнение, например, вариаций двух аналитических методов. Далее описывается, как делаются проверки значимости дисперсий и находятся доверительные интервалы. Однако выполнение этих методов сравнения дисперсий много больше зависит от нормальности распределения исходных данных, чем соответствующие методы сравнения средних.
В главе 1 показано, что, считая верной гипотезу случайного выбора из нормально распределённой популяции, нормированная сумма квадратов отклонений от усреднённого  имеет распределение c2(n–1). Отсюда, в силу (1.13.3), имеем
имеет распределение c2(n–1). Отсюда, в силу (1.13.3), имеем
 =
= ~c2(n–1). (10.6.1)
~c2(n–1). (10.6.1)
Проверка значимости дисперсии
Считалось, что результаты измерений диаметра вала с точностью до сотых долей миллиметра имеют дисперсию s2 не более 10. Для проверки этого сделаны шесть измерений и получен результат s2=13 оценки дисперсии. Допуская, что результаты измерений распределены независимо, одинаково и по нормальному закону, существует ли какое либо важное свидетельство того, что их дисперсия s2 может быть больше 10?
При s2=10 найденное из выражения (10.6.1) значение (n–1)s2/s2=5x13/10=6,5 случайной переменной (х) с распределением c2(5) имеет показанную на Рис.10.6.1 интегральную вероятность Ри=0,739. Эта вероятность находится из выражений
Ри= или Ри=pchisq(х, v),
или Ри=pchisq(х, v),
где х=(n–1)s2/s2, v – число степеней свободы и pchisq(х, v) – встроенная функция Mathcad. Большие чем 6,5 значения переменной (х) имеют вероятность 1–Ри=0,261. Это значение много больше 0,05, поэтому нет смысла ставить под сомнение, что дисперсия s2 может быть больше 10.
Рекомендуемые материалы
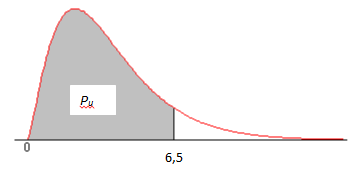
Рис.10.6.1. Графическое изображение интегральной вероятности Ри под кривой функции плотности вероятности распределения c2.
Интервал доверия для дисперсии
Крайние значения интервала доверия с вероятностью 1–α для дисперсии s2 находятся из выражений  и
и  , где крайними значениями интервала доверия являются значения дисперсии, в пределах которых выборочная дисперсия s2 является значимой при принятом уровне вероятности α.
, где крайними значениями интервала доверия являются значения дисперсии, в пределах которых выборочная дисперсия s2 является значимой при принятом уровне вероятности α.
Как и ранее, допустим, получен результат s2=13 оценки дисперсии с использованием пяти степеней свободы. Для дисперсии s2 интервал доверия с вероятностью 0,95 может быть получен следующим образом. В отличие от распределения t здесь невозможно использовать симметрию кривой функции плотности вероятности. Каждое крайнее значение должно вычисляться отдельно. Считая, что интервал доверия имеет интегральную вероятность А=0,95 и показанные на Рис.10.6.2 площади хвостовых частей под кривой одинаковы, то площадь левого хвоста до х0 равна (1–А)/2 и общая площадь под кривой до х1 равна (1–А)/2+А= (1+А)/2.
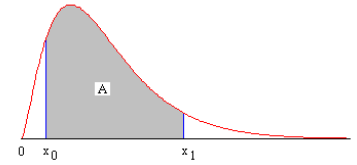
Рис.10.6.2. Графическое изображение интегральной вероятности А интервала доверия под кривой функции плотности вероятности распределения c2.
Тогда, если А=0,95 и v =5, то значения х0 и х1 вычисляются с использованием встроенной в Mathcad обратной кумулятивной функции распределения qchisq(A, v). В результате имеем х0= qchisq[(1–А)/2, v]=0,831 и х1= qchisq[(1+А)/2, v]=12,833. Поэтому искомые крайние значения интервала доверия с вероятностью 0,95 равны
 =
= =5,07 и
=5,07 и  =
= =78,22.
=78,22.
Заметим, что, если число степеней свободы небольшое, то дисперсия и её корень квадратный, то есть, стандартное отклонение, не могут оцениваться очень точно. В качестве грубого приближения, выраженное в процентах от s выборочное стандартное отклонение s равно 100/ [Box с соавт. (2005) стр. 103]. Поэтому, если желательна оценка s с не более чем, например, 5% стандартным отклонением, то необходима выборка примерно из 200 независимых наблюдений!
[Box с соавт. (2005) стр. 103]. Поэтому, если желательна оценка s с не более чем, например, 5% стандартным отклонением, то необходима выборка примерно из 200 независимых наблюдений!
Упражнение 10.6.1. Используя данные упражнения 10.5.9, найдите доверительный интервал с вероятностью 0,90 для дисперсии приведённых данных. Внимательно формулируйте допущения.
Проверка значимости отношения двух дисперсий
Положим, что выборка размером n1 получена случайным образом из популяции наблюдений с нормальным распределением и дисперсией s12, а вторая выборка размером n2 получена случайным выбором из второй популяции наблюдений с нормальным распределением и дисперсией s22. Результаты s12 и s22 оценки дисперсий этих двух популяций вычисляются соответственно с v1 и v2 степенями свободы. При стандартном допущении нормального, независимого и одинакового распределения и, так как, в силу (1.13.4), s12/s12 имеет распределение c2(v1)/v1 и s22/s22 имеет распределение c2(v2)/v2, то отношение [c2(v1)/v1]/[c2(v2)/v2] имеет распределение F(v1, v2). Следовательно, в силу (1.13.5), имеем
 ~F(v1, v2) или эквивалентно
~F(v1, v2) или эквивалентно  ~
~ F(v1, v2).
F(v1, v2).
Например, в результате выполненных неопытным и опытным химиками анализов реплик получены дисперсии выборок соответственно s12=0,183 (при v1=12) и s22=0,062 (при v2=9). Положим, что полученные результаты химиков могут рассматриваться как нормально и независимо распределённые случайные переменные с дисперсиями s12 и s22 и желательно проверить нулевую гипотезу s12=s22 в сравнении с той, что s12>s22. Если нулевая гипотеза s12=s22 верна, то отношение s12/s22 имеет распределение F(12, 9). Значение s12/s22=0,183/0,062=2,95 случайной переменной с распределением F(12, 9) имеет показанную на Рис.10.6.3 интегральную вероятность PF=0,94. Эта вероятность рассчитывается по формулам
PF= или PF=pF(x, v1, v2),
или PF=pF(x, v1, v2),
где х=s12/s22, u – промежуточная переменная и pF(x, v1, v2) – встроенная функция Mathcad.
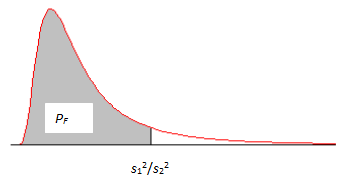
Рис.10.6.3. Графическое представление интегральной вероятности PF под кривой функции плотности вероятности распределения F.
Вероятность, что отношение s12/s22 равно или больше 2,95 получается 1–PF =0,06. Это несколько больше обычно принимаемого уровня вероятности 0,05. Поэтому следует вывод, хотя и не очень убедительный, что работа неопытного химика даёт большую дисперсию.
Интервал доверия для отношения двух дисперсий
Рассуждая также как в случае с одной дисперсией и считая верной гипотезу нормального, независимого и одинакового распределения, значения х0 и х1 имеющей распределение F(v1, v2) переменной являются критическими, имеющими интегральные вероятности соответственно α/2 и 1–α/2, как показано на Рис.10.6.4. Тогда крайние значения интервала доверия с вероятностью 1–α для s12/s22 находятся из выражений
 и
и  .
.
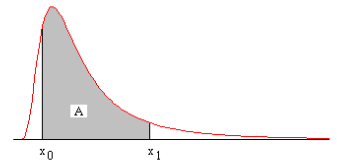
Рис.10.6.4. Графическое изображение интегральной вероятности А интервала доверия под кривой функции плотности вероятности распределения F.
Как и при распределении c2 здесь невозможно использовать симметрию кривой функции плотности вероятности. Каждое крайнее значение должно вычисляться отдельно. Поэтому, считая, что интервал доверия с вероятностью А=0,90 и площади хвостовых частей под кривой функции плотности вероятности распределения F равны, то площадь левого хвоста до х0 равна (1–А)/2 и общая площадь под кривой слева до х1 равна (1+А)/2.
Для вычисления крайних значений интервала доверия с вероятностью А=0,90 для отношения дисперсий s12/s22, как ранее, оценки дисперсий делались соответственно с 12 и 9 степенями свободы и s12/s22=2,95. Критические значения х0 и х1 вычисляются с использованием встроенной в Mathcad обратной кумулятивной функции qF(A, v1, v2) распределения F. В результате имеем х0= qF[(1–А)/2, v1, v2]=0,358 и х1= qF[(1+А)/2, v1, v2] =3,073. Следовательно, искомые крайние значения интервала доверия получаются
 =2,95/3,073=0,96 и
=2,95/3,073=0,96 и  =2,95/0,358=8,24.
=2,95/0,358=8,24.
Зависимость проверок дисперсий от нормальности
Тогда как проверки при сравнении средних нечувствительны к справедливости допущения нормальности распределения исходных данных, это не так для проверок дисперсий (см. сравнения, сделанные для выборочных экспериментов в книге [Box с соавт. (2005) стр. 117]). Иногда можно избежать этой трудности путём преобразования проверки дисперсий в проверку средних [Bartlett, Kendall (1946)]. Логарифм выборочной дисперсии s2 имеет распределение более близкое к нормальному, чем сам результат s2 оценки. Также, при справедливости допущения нормальности, дисперсия log(s2) является независимой от дисперсии s2 популяции. Если имеется некоторое число дисперсий для сравнения, то можно сделать приблизительную проверку, которая нечувствительна к отклонению от нормальности, беря логарифмы выборочных дисперсий и выполняя проверку по этим «наблюдениям» на основе распределения t.
Рассмотрим следующий пример [Box с соавт. (2005) стр.105]. Каждую неделю два аналитика выполняли пять проверок одинаковых выборок из изменяющихся каждую неделю источников. Эти специальные выборки были включены случайным образом в последовательность обычных анализов и не были опознаваемы аналитиками. Вычисленные в результате дисперсии и последующий анализ сведены в таблицу 10.6.1.
Используя сдвоенную проверку на основе распределения t для средних, получаем
 =0,352, sd=0,226 и
=0,352, sd=0,226 и  =sd/
=sd/ =0,101.
=0,101.
Поэтому значение статистики tр с распределением t получается
tр0= =0,352/0,101=3,49.
=0,352/0,101=3,49.
Таблица 10.6.1. Результаты расчёта выборочных дисперсий и их анализ
| Неделя | Аналитик 1 | Аналитик 2 | d=log(100s12)–log(100s22) | ||
| s12 | log(100s12) | s22 | log(100s22) | ||
| 1 | 0,142 | 1,15 | 0,043 | 0,63 | 0,52 |
| 2 | 0,09 | 0,96 | 0,079 | 0,90 | 0,06 |
| 3 | 0,214 | 1,33 | 0,107 | 1,03 | 0,30 |
| 4 | 0,113 | 1,05 | 0,037 | 0,43 | 0,62 |
| 5 | 0,082 | 0,91 | 0,045 | 0,65 | 0,26 |
Допуская естественные изменения анализируемых выборок от недели к неделе, в этом случае выполнялась сдвоенная проверка на основе распределения t. Уровень вероятности Pr(tр≥3,49) для этого значения статистики и распределения t с четырьмя степенями свободы можно найти по формуле
Pr(tр>3,49)=1–pt(3,49, 4)=0,013,
используя компьютерную программу Mathcad. График функции плотности вероятности распределения t симметричен, поэтому требуемая вероятность получается удваиванием ранее полученной вероятности, то есть, она равна вероятности, что значения статистики tр больше +3,49 и меньше –3,49
Pr(|tр|>|tр0|) =2xPr(tр≥3,49) =0,026.
Это значение вероятности является значимым по отношению к уровню вероятности 0,05. Поэтому из двух сравниваемых второй аналитик является более точным.
В этом примере существует естественное разделение данных на группы. Когда это не так, наблюдения могут быть разделены случайно на малые группы и может использоваться этот же подход.
Приложение. Нахождение множества разностей усреднённых
Множество разностей усреднённых на современных компьютерах может быть найдено с использованием программы Microsoft Excel. При этом необходимо использовать язык программирования Visual Basic. В интернете на сайте http://www.get-digital-help.com/2015/02/26/return-all-combinations/ приводится подпрограмма на этом языке для приложений, которая генерирует необходимое число п (=462) комбинаций заданного числа элементов (5 или 6) из общего числа элементов (11). Эта подпрограмма имеет вид:
Public result() As Variant
Function Combinations(rng As Range, n As Single)
rng1 = rng.Value
ReDimresult(n - 1, 0)
Call Recursive(rng1, n, 1, 0)
ReDim Preserve result(UBound(result, 1), UBound(result, 2) - 1)
Combinations = Application.Transpose(result)
End Function
Function Recursive(r As Variant, c As Single, d As Single, e As Single)
Dim f As Single
For f = d To UBound(r, 1)
result(e, UBound(result, 2)) = r(f, 1)
If e = (c - 1) Then
ReDim Preserve result(UBound(result, 1), UBound(result, 2) + 1)
For g = 0 To UBound(result, 1)
result(g, UBound(result, 2)) = result(g, UBound(result, 2) - 1)
Next g
Else
Call Recursive(r, c, f + 1, e + 1)
28 - Эталонная модель взаимодействия открытых систем - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
End If
Next f
End Function
Для её использования необходимо запустить программу Excel и командой Alt+F11 перейти в редактор Visual Basic. В редакторе выбрать мышкой в меню Insert и затем щёлкнуть мышкой по Module. Далее скопировать приведённую выше подпрограмму в окно модуля и выйти из редактора Visual Basic в саму программу Excel.
В Excel сначала необходимо разместить числа строки «Урожаи» таблицы 10.1.3 в строке или столбце ячеек рабочего листа, например в В3:В13. Далее на этом листе выбрать матрицу ячеек, например, Е3:J464. В строке записи формулы ввести обращение к записанной подпрограмме в виде: =Combinations(B3:B13,6). Затем, нажав и держа две клавиши CTRL+SHIFT, нажать клавишу Enter. В результате все 462 комбинации по 6 чисел из строки Урожаи таблицы 10.1.3 появятся в матрице ячеек Е3:J464.
Усреднённые полученных комбинаций находятся с использованием функции =AVERAGE(E3:J3). Для нахождения усреднённых остальных 5 чисел из строки Урожаи таблицы 10.1.3 для 462 комбинаций по 6 чисел необходимо найти общую сумму чисел этой строки и из неё вычесть суммы чисел, полученных в 462 комбинациях по 6 чисел. Полученные результаты поделить на 5 и получить искомые усреднённые остальных 5 чисел. В итоге, вычитанием находится множество разностей усреднённых.





















