Интегральная формула Коши
Лекция 5.
Интегральная формула Коши.
Интегральная формула Коши
|
| Пусть функция
|
Доказательство. По интегральной теореме Коши для многосвязной области
 =
= , где
, где  - окружность с центром в точке
- окружность с центром в точке  , радиусом
, радиусом  ,
,  . Радиус окружности выбран достаточно малым, чтобы окружность целиком лежала в области D. Так как
. Радиус окружности выбран достаточно малым, чтобы окружность целиком лежала в области D. Так как  (важный пример в предыдущей лекции), то
(важный пример в предыдущей лекции), то  . Оценим |
. Оценим | | =
| =
= | |
| 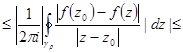

Рекомендуемые материалы
(на окружности  ,
,  , так как
, так как  . По непрерывности функции
. По непрерывности функции  ).
).
 . В силу произвольности
. В силу произвольности  |
| | = 0. Следовательно,
| = 0. Следовательно,  .
.
Теорема. Аналитическая функция является бесконечно дифференцируемой в области аналитичности.
Доказательство. Можно показать, что интеграл в интегральной формуле Коши можно дифференцировать по z0, как по параметру. Проводя это дифференцирование нужное число раз, получим формулу для n – ой производной аналитической функции.
 ,
,  ,
,  ….
….
 . Это - формула для n – ой производной аналитической функции.
. Это - формула для n – ой производной аналитической функции.
Бесплатная лекция: "Лекция 14" также доступна.
С помощью полученных формул (деля обе части на коэффициент перед интегралом) можно вычислять интегралы вида
 ,
,  .
.
Примеры. 1.  (по интегральной формуле Коши)
(по интегральной формуле Коши)
2. (по формуле для первой производной)
(по формуле для первой производной)
3. Вычислить . Аналитичность функции нарушается в точках z=0, z=1. Рассмотрим два контура:
. Аналитичность функции нарушается в точках z=0, z=1. Рассмотрим два контура:  – окружности с центрами в точках z=0, z=1, радиусами r=1/4.
– окружности с центрами в точках z=0, z=1, радиусами r=1/4.  . По интегральной теореме Коши для многосвязной области
. По интегральной теореме Коши для многосвязной области  =
=  +
+ =
=  =
=
= .
.



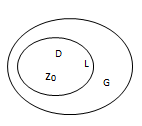
 аналитическая в односвязной области G . Пусть кусочно-гладкий контур L принадлежит G вместе со своей внутренностью D . Пусть
аналитическая в односвязной области G . Пусть кусочно-гладкий контур L принадлежит G вместе со своей внутренностью D . Пусть  , тогда
, тогда 



















