Преобразование Фурье

Лекция 5.

Преобразование Фурье.

Ряд Фурье в комплексной форме.

     =

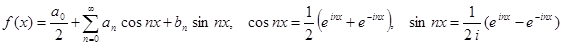
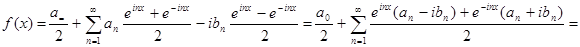
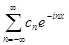
Рекомендуемые материалы

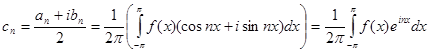
Следовательно, .

Интеграл Фурье.

Теорема. Пусть 1) ограничена на R, 2)  абсолютно интегрируема на R, 3)на любом конечном интервале  удовлетворяет условиям Дирихле. Тогда

,     .

Вывод (нестрогий). Рассмотрим разложение функции в ряд Фурье на .

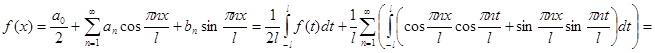
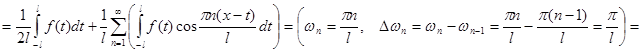
. Перейдем  к пределу при . Так как , то .

Второе слагаемое при  переходит в  (предел интегральной суммы). Следовательно, в точках непрерывности

.

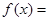
Косинус и синус – преобразования Фурье.

Заметим, что подынтегральная функция в интеграле Фурье четна по . Поэтому

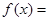
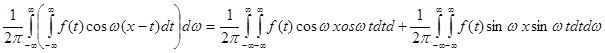
1) Пусть  - четная функция, тогда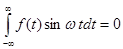

В точках непрерывности =.

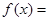
- обратное косинус – преобразование Фурье

- косинус – преобразование Фурье.

2) Пусть  - нечетная функция, тогда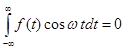

=.

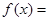
- обратное синус – преобразование Фурье

- синус – преобразование Фурье.

Преобразование Фурье.

Из формулы интеграла Фурье по четности подынтегральной функции по  имеем

= =

+.

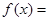
Рассмотрим второй интеграл и сделаем в нем замену .

= =

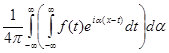
Получили первый интеграл, следовательно, второй интеграл равен первому. Поэтому

== .

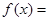
Лекция "Внешняя политика Ивана III" также может быть Вам полезна.

 называются прямым и обратным преобразованием Фурье.

Часто множитель относят ко второму интегралу:

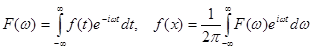
Связь преобразований Лапласа и Фурье.

Запишем преобразование Лапласа =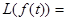

= . Таким образом, преобразование Лапласа функции  есть преобразование Фурье функции . Заметим, что ограниченность функции  следует из выполнения требования к оригиналу по Лапласу : . Тогда ||< .