Векторная функция скалярного аргумента и её производная

Векторная функция скалярного аргумента:  и её производная. Касательная к пространственной кривой. Теорема о производной вектор-функции постоянной длины.

Рассмотрим [a,b]. Пусть любому поставлен в соответствии некоторый вектор , тогда говорят, что на [a,b] задана векторная функция скалярного аргумента.

Пусть задана ортонормированная система координат с базисом , тогда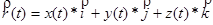

Функции x(t), y(t), z(t)- скалярные функции действительного аргумента – координатные функции для вектор-функции .

Геометрический смысл векторной функции:

Функции соответствует некоторая кривая

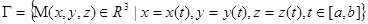
Такое представление кривой называют годографом.  называется пределом функции скалярного аргумента при  если:

.

Рекомендуемые материалы

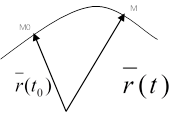
Рассмотрим приращение векторной функции, придадим t приращение , тогда

.

Производной в точке  называется предел разностного отношения при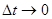

, .

, .

7 Журналист и современная система телевидения - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

=

=

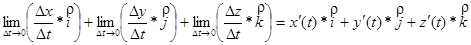
Пусть . Предельное положение секущей  при  называют касательной к кривой Г в точке .  . Тогда при  касательная в точке  параллельна вектору . Уравнение касательной: .

- каноническое уравнение касательной.

Теорема: Пусть векторная функция скалярного аргумента ,  - является непрерывно-дифференцируемой функцией на , которой соответствует некоторая кривая Г: . Тогда длина дуги Г удовлетворяет:  (при этом Г имеет конечную длину).

Доказательство: , где , по условию теоремы, функция непрерывно-дифференцируема, значит  на отрезке  - непрерывная функция. ,  (по 1 теореме Вейерштрасса). при.