Определение объема выборки
5. Определение объема выборки
При ограниченном бюджете объем выборки
n = (общий бюджет обследования) / (стоимость одного интервью)
5.1. Заданная точность по количественной переменной
1. Требуется оценить среднее  с помощью
с помощью  с заданной абсолютной погрешностью (L) половины длины доверительного интервала на уровне значимости
с заданной абсолютной погрешностью (L) половины длины доверительного интервала на уровне значимости  :
:
 ,
,
где  - квантиль порядка
- квантиль порядка  нормального закона распределения N(0,1).
нормального закона распределения N(0,1).
Рекомендуемые материалы
Тогда, решив неравенство, получаем
 , при
, при 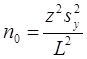
Если  , то
, то  .
.
Пример 4.
В условиях примера 1 определим необходимый объем выборки, для которого с 90-% доверительной вероятностью истинное среднее значение числа свободных мест на авиарейсах не отличалось бы от оценки более чем на 0,1.
Решение.
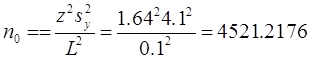
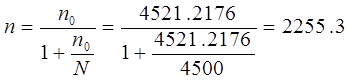
Следовательно объем выборки n должен составлять не менее 2256.
Пусть требуется оценить среднее  с помощью
с помощью  с заданной относительной погрешностью
с заданной относительной погрешностью  . Тогда
. Тогда
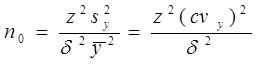
Замечание: или
или  должны быть известны априори
должны быть известны априори
(заранее), например, на основе:
· предыдущего обследования этой же совокупности;
· обследования по переменной x, коррелированной с y,
· мнения экспертов;
· обследования аналогичной совокупности по другому региону:
· результатов пилотного обследования
5.2. Заданная точность для оценки доли
1. Требуется оценить долю элементов в совокупности P с помощью доли p в выборке с заданной абсолютной погрешностью L :

Следовательно:
 , при
, при 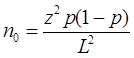
Если  , то
, то  .
.
Замечание.
Как и в предыдущем случае уровень доли p должен быть известен заранее.
При самых неблагоприятных условиях:
p = 0.5 и 
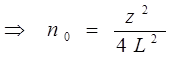
2. Требуется оценить долю P, с помощью p, с заданной относительной Погрешностью  :
:
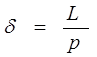
Следовательно:
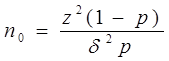
3. Комментарии
При практическом определении объема выборки:
® В случае нескольких изучаемых переменных возникает необходимость компромиссного решения;
® Если возможны неответы респондентов, то нужно к рассчитанному теоретически объему выборки «добавлять» процент неответов.
® Если неизвестное значение доли p мало (p < 10%) и требуется обеспечить заданную относительную погрешность результатов, тогда можно воспользоваться процедурой «целевого» случайного отбора.
Процедура «целенаправленного» случайного отбора.
Если доля P мала, то можно положить:
 .
.
Откуда получаем

m - количество единиц в выборке, обладающих нужной характеристикой.
Поэтому случайный отбор продолжают до получения m единиц с нужной характеристикой.
Так как случайный объем выборки n следует закону отрицательного гипергеометрического распределения, то оценить долю P и рассчитать оценку дисперсии можно с помощью следующих формул;
*  - несмещенная оценка доли P;
- несмещенная оценка доли P;
*  - несмещенная оценка дисперсии.
- несмещенная оценка дисперсии.
Пример 6.
Пусть с заданной относительной погрешностью ( ) равной 0,1 требуется оценить долю состоятельных домохозяек в женской зрительской аудитории некоторой программы телеканала.
) равной 0,1 требуется оценить долю состоятельных домохозяек в женской зрительской аудитории некоторой программы телеканала.
Примечание.
Этот уровень относительной погрешности обеспечивает 1%-ую предельную ошибку оценки доли при  :
:
Характеристика процесса нагревания и охлаждения воды в озерах - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Так как интересующая доля P мала, то

m - количество единиц в выборке объема n, обладающих нужной характеристикой.
Поэтому случайный отбор следует продолжать до тех пор, пока в выборке не окажется 385 состоятельных домохозяек.




















