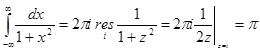Вычисление несобственных интегралов с помощью вычетов

Вычисление несобственных интегралов с помощью вычетов

Теорема. Если   при x=z, -изолированная особая точка f(z),  имеет в  нуль не ниже II порядка,  не имеет особых точек на действительной оси,   имеет конечное число особых точек, то , где распространяется на особые точки, лежащие выше действительной оси.

Док-во:

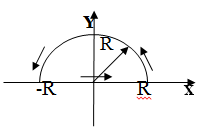
Возьмем круг такого радиуса, чтобы на нем и вне его не было особых точек, кроме бесконечности.

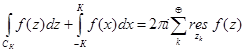
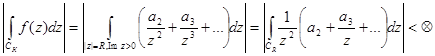
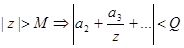
Если Вам понравилась эта лекция, то понравится и эта - 9.1 Эпоха Средневековья.

.

Пример. Найти интеграл:.

, ;