Тройной интеграл

16.2. Тройной интеграл.

    

16.2.1. Определение тройного интеграла. Теорема существования тройного интеграла. Пусть в пространстве Oxyz задана ограниченная замкнутая область (объём)  V, и пусть на области V определена функция .

Разобьём область V произвольным образом на  подобластей  (не имеющих общих внутренних точек). Символом  будем обозначать объём области ; символом  обозначим наибольший из диаметров областей : .

В каждой из подобластей  выберем произвольную точку , вычислим в этой точке значение функции , и составим интегральную сумму  .

            Если существует предел последовательности интегральных сумм при , не зависящий ни от способа разбиения области V на подобласти , ни от выбора точек , то функция  называется интегрируемой по области V, а значение этого предела называется тройным интегралом от функции  по области V и обозначается .

            Если расписать значение  через координаты точки , и представить  как , получим другое обозначение тройного интеграла: . Итак, кратко, .

            Теорема существования тройного интеграла. Если подынтегральная функция  непрерывна на области V, то она интегрируема по этой области.

16.2.2. Свойства тройного интеграла по смыслу и доказательству полностью аналогичны свойствам определённого и двойного интегралов.

Рекомендуемые материалы

16.2.2.1. Линейность. Если функции ,  интегрируемы по области V, то их линейная комбинация  тоже интегрируема по , и  .

16.2.2.2. Аддитивность. Если область  является объединением двух областей  и , не имеющих общих внутренних точек, то .

16.2.2.3. Интеграл от единичной функции по области V равен объёму этой области: .

16.2.2.4 Интегрирование неравенств. Если в любой точке  выполняется неравенство , и функции  интегрируемы по области V, то .

16.2.2.3. Теоремы об оценке интеграла.

16.2.2.4.1. Если функция  интегрируема по области V, и для  выполняется , то .

16.2.2.4.2.  Если функция  интегрируема по областиV,  то .

16.2.2.5. Теорема о среднем. Если функция  непрерывна на области V,  то существует точка , такая что .

16.2.3. Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному.  Будем называть ограниченную замкнутую область V простой (правильной), если выполняются два условия : проекция V  на какую-либо координатную плоскость, например, на плоскость Оху - простая область D, и любая прямая, перпендикулярная этой плоскости и проходящая через внутреннюю точку V, пересекает границу V в двух точках. Такую область можно описать следующим образом:  (поверхность  образована множеством нижних точек пересечения прямой, параллельной оси Oz, с границей V; поверхность  - множеством верхних точек пересечения).

Теорема. Если V - простая область с кусочно-гладкой границей,  - непрерывная функция, то .

Доказать эту теорему можно так, как мы доказали теорему о переходе от двойного интеграла к повторному: установить, что для повторного интеграла в правой части формулы имеют место все свойства интеграла, разбить область V на подобласти , пользуюсь свойствами аддитивности и теоремой о среднем, представить повторный интеграл как интегральную сумму для тройного  и перейти к пределу при .

Если расписать двойной интеграл по простой области D  в виде повторного, получим ещё более детализированную формулу для вычисления тройного интеграла: .

Можно также доказать, что тройной интеграл можно представить в виде повторного с другим порядком интегрирования. Обозначим  (т.е. минимальное и максимальное значения ординаты для точек области V),  - плоскую область, получающуюся при сечении V плоскостью . Тогда . Естественно, для конкретной задачи может оказаться предпочтительней проектировать V не на плоскость Оху, а на другую координатную плоскость.

         

16.2.4. Примеры. 1.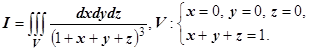

Проекция области  V на плоскость Оху -  треугольник , поэтому

.

    

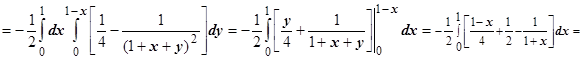
2.  Здесь V - внутренность конуса, D - проекция круга, получающегося при сечении этого конуса плоскостью  на Оху, т.е. круг, ограниченный кривой , поэтому

 (переходим к полярным координатам)   .

            Вычислим тот же интеграл по другой формуле перехода к повторному интегралу:  (внутренний двойной интеграл - интеграл от функции, равной 1, поэтому он равен площади круга, получающегося при сечении конуса плоскостью , уравнение  ограничивающей окружности , площадь ) = .  Это решение оказалось проще; мы сыграли на том, что подынтегральная функция не зависит от х и у.

16.2.5. Замена переменных в тройном интеграле.

16.2.5.1. Теорема о за мена переменных в тройном интеграле. Пусть в пространстве Ouvw задана область G, и пусть отображение  преобразует эту область в область V   пространства Oxyz.  Будем считать, что отображение F задаётся функциями . Пусть: 1). F взаимно однозначно отображает G на V; 2). Функции x(u,v,w), y(u,v,w), z(u,v,w)  непрерывно дифференцируемы на G (имеют непрерывные частные производные); 3). Якобиан  не обращается в нуль на G.  Тогда .

Доказательство этой теоремы аналогично доказательству теоремы о замене переменных в двойном интеграле.

            Рассмотрим наиболее часто употребляемые криволинейные системы координат в пространстве - цилиндрические и сферические.

          

16.2.5.2. Тройной интеграл в цилиндрических координатах. В этой координатной системе положение точки в пространстве характеризуется тремя числами: r, j и z, где r и j - полярные координаты проекции M¹

точки М на плоскость Оху, z - аппликата точки M. Формулы перехода от цилиндрических координат к декартовым:

             

Вычислим якобиан этого преобразования: , следовательно, .

16.2.5.3. Тройной интеграл в сферических координатах. В этих координатах положение точки M в пространстве характеризуется тремя числами: r, j и , где r - длина радиуса-вектора точки M, j - полярный угол проекции M¹ точки М на плоскость Оху,  - угол между радиусом-вектором точки M и осью Oz. Формулы перехода от сферических координат к декартовым:

             

Вычислим якобиан этого преобразования:   , следовательно, .

            16.2.5.4. Примеры применения цилиндрических и сферических координат. Как и в случае перехода к полярным координатам в двойном интеграле, дать однозначный рецепт того, когда следует применять цилиндрические или сферические координаты, нельзя, это дело опыта. Можно попробовать применить цилиндрические координаты, если подынтегральная функция и/или уравнения поверхностей, ограничивающих объём V, зависят от комбинации ; сферические - если эти уравнения зависят от . Рассмотрим ряд примеров.

            1. Найти объём V общей части двух шаров, ограниченных сферами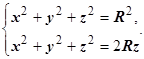

         

Решение. Пересечение сфер находится на уровне 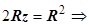  и представляет собой круг радиуса . Объём V ограничен сверху поверхностью , снизу - поверхностью . Вычисления в декартовых координатах дают  - достаточно громоздкие выкладки. В цилиндрических координатах объём V ограничен сверху поверхностью , снизу - поверхностью , поэтому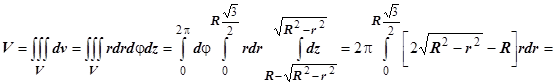

.

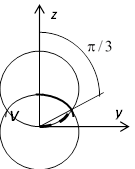
В сферических координатах уравнение нижней сферы принимает вид , верхней - , их пересечение соответствует значению . В интервале  r меняется от 0 до R, в интервале  r меняется от 0 до , поэтому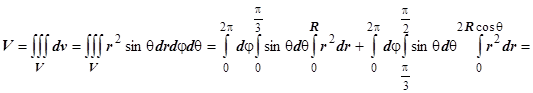

.

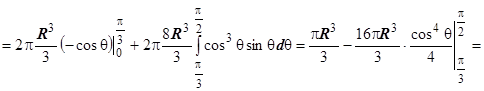
В этом примере трудоёмкость вычислений в цилиндрических и сферических координатах примерно одинакова.

2. 

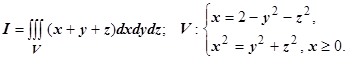
Параболоид и конус пересекаются в плоскости  по кругу радиуса 1. Осью симметрии объёма V служит ось Ох, поэтому цилиндрические координаты вводим формулами   

.

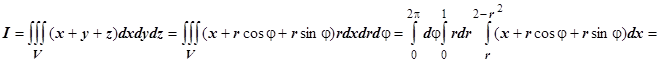
Применение сферических координат в этом примере нецелесообразно (громоздкое уравнение для параболоида).

            3.  Здесь область интегрирования - шар радиуса 1/2, сдвинутый по оси Оz на 1/2 единицы, подынтегральная функция зависит от выражения , поэтому применим сферические координаты. Уравнение сферы  , поэтому .

  

4. Вычислить объём тела, ограниченного поверхностью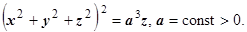

Здесь тоже для того, чтобы понять, как устроено тело, и найти его объём, надо перейти к сферическим координатам (на это указывает комбинация ). Уравнение поверхности . По этому уравнению поверхность построить уже можно; отсутствие координаты  в уравнении показывает, что это - тело вращения вокруг оси Oz. Находим объём:

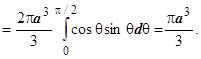
            16.2.6. Механические приложения тройного интеграла. Пусть V - тело в пространстве, в котором задано распределение объёмной плотности массы  (,, где G - область, содержащая точку Р,  - масса этой области,  - её объём). Вывод следующих формул полностью аналогичен выводу для двумерного случая (раздел 16.1.7.4. Механические приложения двойного интеграла), поэтому просто перечислим их.

 Масса тела;

координаты центра тяжести , , ;

моменты инерции  (относительно плоскости Oxz),   (относительно плоскости Oyz),  (относительно плоскости  Oxy),  (относительно оси Ox),  (относительно оси Oy),  (относительно оси Oz),   (относительно начала координат).

 

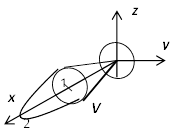
Примеры. 1. Найти координаты центра тяжести половины шара радиуса , если плотность пропорциональна расстоянию от центра шара.

            Решение. Если ввести координатную систему так, как показано

на рисунке, то ; вычисления ведём, естественно, в сферических координатах:

; , аналогично  (что, впрочем, очевидно и без вычислений); .

Вместе с этой лекцией читают "5.8. Обзор рынка программных продуктов".

 

2. Найти моменты инерции однородного  цилиндра относительно диаметра основания и оси.

            Решение. Если система координат введена так, как показано на рисунке, то мы должны найти  (или ) и . Вычисляем в цилиндрических координатах.

.

.
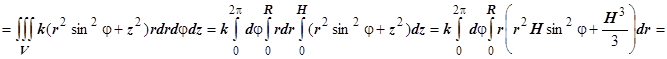