Двойной интеграл

16.1. Двойной интеграл.

            16.1.1. Определение двойного интеграла. Теорема существования двойного интеграла.

Пусть на плоскости Oxy задана ограниченная замкнутая область D с кусочно-гладкой границей, и пусть на области D определена функция .

Разобьём область D произвольным образом на  подобластей  (не имеющих общих внутренних точек). Символом  будем обозначать площадь области ; символом  здесь и дальше будет обозначаться наибольшее расстояние между двумя точками, принадлежащими области D:

;

символом  обозначим наибольший из диаметров областей : .

В каждой из подобластей  выберем произвольную точку , вычислим в этой точке значение функции , и составим интегральную сумму  .

            Если существует предел последовательности интегральных сумм при , не зависящий ни от способа разбиения области D на подобласти , ни от выбора точек , то функция  называется интегрируемой по области D, а значение этого предела называется двойным интегралом от функции  по области D и обозначается .

Рекомендуемые материалы

            Если расписать значение  через координаты точки , и представить  как , получим другое обозначение двойного интеграла: . Итак, кратко, .

            Теорема существования двойного интеграла. Если подынтегральная функция  непрерывна на области D, то она интегрируема по этой области.

16.1.2. Геометрический смысл двойного интеграла. Геометрический смысл каждого слагаемого интегральной суммы: если , то   - объём прямого цилиндра с основанием  высоты ; вся интегральная сумма  - сумма объёмов таких цилиндров, т.е. объём некоторого ступенчатого тела (высота ступеньки, расположенной над подобластью , равна ). Когда , это ступенчатое тело становится всё ближе к изображенному на рисунке телу, ограниченному снизу областью , сверху - поверхностью , с цилиндрической боковой поверхностью, направляющей которой является граница области , а образующие параллельны оси . Двойной интеграл  равен объёму этого тела.

16.1.3. Свойства двойного интеграла.

16.1.3.1. Линейность. Если функции ,  интегрируемы по области , то их линейная комбинация  тоже интегрируема по области , и  .

Док-во. Для интегральных сумм справедливо равенство   . Переходя к пределу при  и пользуясь свойствами пределов, рассмотренными в разделе 4.4.6. Арифметические действия с пределами (конкретно, свойствами 4.4.10.1 и 4.4.10.2), получим требуемое равенство.

16.1.3.2. Аддитивность. Если область  является объединением двух областей  и , не имеющих общих внутренних точек, то .

Док-во. Пусть область  разбита на подобласти , область  разбита на подобласти . Тогда объединение этих разбиений даст разбиение области :  на  подобластей. Интегральная сумма по области  равна сумме сумм по областям  и : . Как и в предыдущем случае, переходя к пределу при , получим требуемое равенство.

16.1.3.3.Интеграл от единичной функции по области  равен площади этой области: .

Док-во: Для любого разбиения , т.е. не зависит ни от разбиения, ни от выбора точек . Предел постоянной равен этой постоянной, поэтому .

16.1.3.4. Интегрирование неравенств. Если в любой точке  выполняется неравенство , и функции  интегрируемы по области , то .

            Док-во. В любой точке  выполняется неравенство , поэтому . По теореме о переходе к пределу в неравенствах отсюда следует требуемое утверждение.

16.1.3.5. Теоремы об оценке интеграла.

16.1.3.5.1. Если функция  интегрируема по области , и для  выполняется , то .

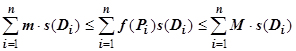
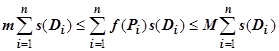
Док-во.     (цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств).

16.1.3.5.2. Если функция  интегрируема по области , то .

Док-во. Эти неравенства непосредственно следуют из того, что  и свойства 16.1.3.4. Интегрирование неравенств.

16.1.3.6. Теорема о среднем. Если функция  непрерывна на области ,  то существует точка , такая что .

Док-во. Непрерывная на ограниченной замкнутой области  функция  принимает в некоторых точках этой области своё минимальное  и максимальное  значения. Так как , то , или . Непрерывная функция принимает, кроме того, любое значение, заключённое между   и , в частности, значение . Следовательно, , откуда и следует доказываемое утверждение.

16.1.4. Вычисление двойного интеграла. Двукратный (повторный) интеграл.

16.1.4.1. Определение простой (правильной) области.  Область  на плоскости Oxy будем называть простой (правильной) в направлении оси Oy, если любая прямая, проходящая через внутреннюю точку области  и параллельная оси Oy, пересекает границу  в двух точках.

            Аналогично определяется область, простая (правильная) в направлении оси Ox: любая прямая, проходящая через внутреннюю точку области  и параллельная оси Oх, пересекает границу  в двух точках.

            Область, правильную (простую) в направлении обеих осей, будем называть правильной.

Ограниченную замкнутую область , правильную в направлении оси Oy, можно описать неравенствами . Числа  и  существуют вследствие ограниченности области , функция  образована нижними точками пересечения прямой  при  с границей области , функция  - верхними точками пересечения этой прямой с границей области :

            Аналогичным образом область , ограниченную, замкнутую и правильную в направлении оси Oх, можно описать неравенствами . Функция  образована левыми точками пересечения прямой  при  с границей области , функция  - правыми точками пересечения этой прямой с границей области .

      

Для правильной области (т.е. области, правильной в направлении обеих осей) существуют оба способа представления: и , и .

16.1.4.2. Двукратный (повторный) интеграл. Пусть  - область, простая в направлении оси Oy. Рассмотрим выражение . Эта конструкция определяется через два обычных определённых интеграла. После интегрирования по у во внутреннем интеграле (переменная х при этом рассматривается как постоянная) и подстановки по у в пределах от  до  получается функция, зависящая только от х, которая интегрируется в пределах от a до b. В дальнейшем мы будем обычно записывать этот объект без внутренних скобок:

.

Можно показать, что двукратный интеграл обладает всеми свойствами двойного интеграла:

Свойства линейности и интегрирования неравенств следуют из этих свойств определённого интеграла; интеграл от единичной функции даёт площадь области: ; теоремы об оценке и о среднем следуют из перечисленных свойств. Единственное свойство, с которым придётся повозиться - это свойство аддитивности. Мы докажем его в простой, но достаточной для нас форме: если область  разбита на две подобласти  и  прямой, параллельной одной из координатных осей, то двукратный интеграл по области  равен сумме интегралов по   и : .

      

Первый случай: прямая  параллельна оси Oy. Тогда  (аддитивность внешнего интеграла) .

            Второй случай: прямая  параллельна оси Oх. Воспользуемся сначала аддитивностью внешнего интеграла:

(теперь применим свойство аддитивности для внутреннего интеграла в среднем слагаемом) =  (применяем свойство линейности для внешнего интеграла в среднем слагаемом и перегруппировываем сумму)=

(первая фигурная скобка даёт повторный интеграл по , второй - по ) .

      

Понятно, что воэможны различные случаи взаимного расположения прямых , ,  и функций , , но логика доказательства во всех случаях такая же.

            Обобщим доказанное свойство. Пусть прямая разбивает область  на две подобласти   и . Проведём ещё одну прямую, параллельную какой-либо координатной оси. Пусть эта прямая разбивает  на  и;  - на  и . По доказанному, , , поэтому . Продолжая рассуждать также, убеждаемся в справедливости следующего утверждения: если область  с помощью прямых, параллельных координатным осям, разбита на подобласти , то .

16.1.4.3. Теорема о переходе от двойного интеграла к повторному. Пусть  - простая в направлении оси Oy область. Тогда двойной интеграл от непрерывной функции по области  равна повторному интегралу от той же функции по области : .

Док-во. Разобьём область  с помощью прямых, параллельных координатным осям, на подобласти . По доказанному выше, . К каждому из итегралов  применим теорему о среднем: в любой области  найдётся точка  такая, что . Следовательно, . В последнем равенстве справа стоит интегральная сумма для двойного интеграла . Будем мельчить разбиение области так, чтобы . Вследствие непрерывности функции  по теореме существования интегральная сумма при этом стремится к двойному интегралу , т.е. в пределе получим , что и требовалось доказать.

Если область правильная в направлении оси Oх, то аналогично доказывается формула . Если правильна в направлении обеих осей, то для вычисления двойного интеграла можно применять любую из эти формул: .

Если область не является правильной, её разбивают на правильные подобласти.

16.1.5. Замена переменных в  двойном интеграле.  Двойной интеграл в полярных координатах.

16.1.5.1.Теорема о замене переменных в двойном интеграле. Пусть на плоскости Ouv задана область G, и пусть отображение  преобразует эту область в область D  на плоскости Oxy.  Будем считать, что отображение F задаётся функциями . Пусть: 1). F взаимно однозначно отображает G на D; 2). функции x(u,v), y(u,v) непрерывно дифференцируемы на G (имеют непрерывные частные производные); 3). якобиан  не обращается в нуль на G. Докажем, что в этих предположениях .

Док-во. 1. Рассмотрим, как связаны между собой площадь параллелограмма АВСЕ со сторонами  в области G и площадь его образа при преобразовании F  - криволинейного параллелограмма  в области D. С точностью до бесконечно малых высших порядков по сравнению с , площадь криволинейного параллелограмма   равна площади обычного параллелограмма, построенного на векторах  и . Пусть точка А имеет координаты (u,v), тогда точка А₁ будет иметь координаты (x(u,v),y(u,v)), т.е. . Для других точек:   (по формуле приращения дифференцируемой функции). Аналогично

, где  при . Пренебрежём членами порядка малости выше первого по сравнению с . Тогда .

Пусть теперь i,j,k - базисные орты пространства, в котором лежит плоскость Oxy. Как известно, площадь параллелограмма, построенного на векторах  и , равна модулю векторного произведения этих векторов (проекции на орт k равны нулю):

.

Мы доказали замечательную вещь. Если вокруг точки  взять маленькую область, то после преобразования F площадь этой области меняется в  раз.

 

            2. Перейдём к доказательству основной формулы. Разобьём G прямыми, параллельными осям координат, на области . Образы этих линий дадут разбиение D  на области . Для этого разбиения составим интегральную cумму . Устремим ; тогда и . И слева, и справа интегральные суммы записаны для непрерывных функций, следовательно,и слева, и справа существуют пределы - двойные интегралы, и они равны: , что и требовалось доказать.

            16.1.5.2. Двойной интеграл в полярных координатах. Нам придётся применять эту формулу, в основном, для перехода к полярным координатам. Роль переменных u и v будут играть r и . Как известно, . Вычислим якобиан: , следовательно, . Двойной интеграл в координатах r, вычисляется также как и в координатах x,y, переходом к двухкратному, при этом внешний обычно берут по . Если область D описывается как , то . Естественно, если  - кусочные функции, то внешний интеграл разбивается на несколько слагаемых. Однозначно дать рецепт, когда имеет смысл переходить к полярным координатам, нельзя, это дело опыта. Можно пробовать перейти к r,, если либо f(x,y), либо кривые, ограничивающие область интегрирования, либо и то, и другое вместе, зависят от комбинации .

   

Если  и/или область D ограничивается эллипсом , полезны обобщённые полярные координаты . Каков якобиан этого преобразования?

16.1.6. Задачи на двойной интеграл.

16.1.6.1. Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам. Смысл этих задач - научиться быстро определять параметры  (в декартовых координатах) и  (в полярных координатах), необходимые для перехода от двойного интеграла к повторному. Примеры:

1. Пусть область  . Представить двойной интеграл по области  в виде повторных. Перейти к полярным координатам.

Решение: область изображена на рисунке справа. Для левой части  ; для правой -  (уравнение правой полуокружности после выделения полных квадратов принимает вид ), поэтому .  можно также описать неравенствами , поэтому . В полярных координатах уравнение левой четверти окружности имеет вид  для  (можно взять и отрезок ), правой полуокружности  для  (можно взять и отрезок ), поэтому .

2. . Изменить порядок интегрирования, перейти к полярным координатам.

Решение. Область  - объединение трёх подобластей:  . На рисунке изображена область и приведены уравнения прямых и обратных функций для линий, ограничивающих её.  можно представить в виде , поэтому . В полярных координатах  представляется как объединение двух треугольников OCB и OBA. Уравнение прямой ОС:  (можно получить и формально, перейдя к полярным координатам в её уравнении:  ), прямой ОВ: , прямой СВ:  , прямой ОА: , прямой АВ:  . В результате  .

16.1.6.2. Вычисление двойного интеграла. Двойной интеграл вычисляется переходом к повторному. Рассмотрим ряд примеров.

1. .

Здесь область  (которую обязательно надо изобразить на чертеже) правильна в направлении обеих осей, поэтому вычисления по обеим формулам перехода имеют одинаковую трудоёмкость:

;

.

            2. .

Здесь область  тоже правильна в направлении обеих осей, однако верхняя граница состоит из двух кусков: , поэтому первый из повторных интегралов будет содержать два слагаемых:

;

Этот пример проще решается по второй формуле.

3. .

Здесь переход к повторному интегралу по формуле  бессмысленен, так как внутренний интеграл не берётся, в то же время второй повторный интеграл вычисляется без проблем:

4.

Здесь область D ограничена окружностью радиуса а, сдвинутой на а единиц по оси Ох. Уравнения для правой, левой, верхней и нижней полуокружностей приведены на рисунке. Повторные интегралы в декартовых координатах

,  можно вычислить, но это достаточно трудоёмко. Попробуем перейти к полярным координатам (это имеет смысл, так как и подынтегральная функция, и кривая, ограничивающая D зависят от выражения ). Переход к полярным координатам в уравнении окружности даёт , или . Это и есть уравнение границы в полярных координатах. Итак,

Ответ явно неправильный. Мы должны получить объём тела, расположенного в полупространстве , ограниченного цилиндром  и сферой  радиуса  сверху; в то время как получили половину объём верхнего полушара (рисунок справа). С такой ситуацией мы уже встречались, когда рассматривали приложения определённого интеграла. Ошибка делается, когда выражение  заменяется на , а не на . Дальше необходимо отдельно рассматривать интервалы  и . Избежать это можно, если воспользоваться симметрией и области, и подынтегральной функции относительно оси Ох, т.е. вычислять удвоенный интеграл по половине круга :

 

16.1.7. Приложения двойного интеграла.

      

16.1.7.1. Вычисление площадей плоских областей. В соответствии с свойством 16.1.3.3. Интеграл от единичной функции . Пример: найти площадь области , лежащей внутри кривых .

            Решение. Построить эти кривые можно только в полярных координатах; первое уравнение приводится к виду , это - лемниската Бернулли; второе - к виду , это - кардиоида. Решая уравнение , находим, что точка их пересечения лежит на луче . D состоит из двух лунок одинаковой площади; вычислим площадь верхней. При эта лунка ограничена кардиоидой; при  - лемнискатой, поэтому  

 

 ё

            16.1.7.2. Вычисление объёмов. Объём тела, ограниченного сверху и снизу поверхностями , , , с боков - цилиндрической поверхностью с образующими, параллельными оси , равен ; эта формула очевидно следует из геометрического смысла двойного интеграла. Основной вопрос, который надо решить - на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.

   

Примеры. 1. Найти объём тела

Решение. Тело изображено на рисунке справа. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось Oxz:  Область D - треугольник, ограниченный прямыми , поэтому  

.

2. Найти объём области, ограниченной поверхностями  .

Решение. Первая поверхность - сфера, вторая - цилиндрическая - с образующими, параллельными оси Oz (в уравнении нет z в явной форме). Построить в плоскости Oxy кривую шестого порядка, заданную уравнением , в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей (чётные степени) и точка О(0,0) принадлежит этой кривой. Пробуем перейти к полярным координатам.

 Эту кривую построить уже можно.  максимально, когда , минимально, когда

, и гладко меняется между этими пределами (точка О(0,0) не принадлежит этой кривой, где мы её потеряли?).

Пользуясь симметрией, получаем

 

 и т.д.

         

16.1.7.3. Вычисление площади поверхности. Пусть в пространстве задана кусочно-гладкая поверхность , однозначно проектирующаяся в область D на плоскости Оху. Пусть эта поверхность задаётся уравнением . Тогда площадь этой поверхности выражается формулой

.

Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром  из сферы .

Решение. На рисунке изображён верхний из этих лепестков. Уравнение поверхности  вычисляем производные   и . Область D - сдвинутый на а единиц по оси Ох круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей Оху и Охz:  .

            16.1.7.4. Механические приложения двойного интеграла должны решит. Будем считать, что D - неоднородная плоская пластина с поверхностной плотностью материала в точке Р равной . В механике  определяется так. Точка Р окружается малой областью S, находится масса  и площадь этой области (площадь тоже будем обозначать буквой S), и . Для нахождения массы по заданной плотности мы ь обратную задачу. Разобьём D на малые подобласти , в каждой из подобластей  выберем произвольную точку , и, считая что в пределах  плотность постоянна и равна , получим, что масса  приближённо есть , а масса всей пластины . Это - интегральная сумма, при уменьшении  точность приближения увеличивается, и в пределе .

            Аналогично находятся другие параметры пластины:

координаты центра тяжести , ;

моменты инерции  (относительно оси Ox),  (относительно оси Oy),  (относительно начала координат).

   

Пример: найти параметры неоднородной плоской пластины, ограниченной кривыми  если плотность .

            Решение.

К.Ясперс про осевое время, смысл и назначение истории - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

  (что и следовало ожидать, так как область и плотность симметричны относительно оси Оу).

.

.            .