Производная обратной и неявной функций

Производная обратной и неявной функций

            Относительно функции  может быть поставлена такая проблема: существует ли (и если да, то единственная ли) такая функция , что для всякого  из области определения функции 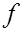. Функция  в этом случае, коль скоро она существует, называется обратной к 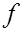, а сама функция 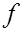тогда называется обратимой.

            Для линейной функции вопрос об обратимости решается, как известно, следующим образом: функция обратима тогда и только тогда, когда она является изоморфизмом одного евклидова пространства на другое (см. п. 1.8, теорема 1.2). В конечномерном случае ответ может быть дан в терминах матричной алгебры: линейный оператор обратим тогда и только тогда, когда в любой паре базисов его матрица обратима (для этого достаточно, чтобы матрица было обратима в какой-нибудь одной паре базисов).

            В нелинейном случае проблема обратимости (и. что существенно, проблема единственности ее решения) сильно усложняется - это видно на примере тригонометрических функций.

            В этом параграфе мы без строгих доказательств обсудим проблему обратимости для нелинейных векторных функций и вместе с ней проблему дифференцируемости обратной функции, когда она существует.

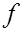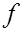            Пусть функция такова, что , т.е. размерности пространств совпадают. Пусть также в некоторой точке  функция дифференцируема. Запишем тогда ее приращение в этой точке:

                                                  (1)

Пренебрегая бесконечно малым по норме( по сравнению с нормой приращения аргумента  ) вектором  и обозначая приращение функции в точке через , получим

                                                                                (2)

Рекомендуемые материалы

            Рассмотрим (2) как векторное уравнение относительно неизвестного вектора . Нетрудно понять, что в матричной форме это будет не что иное, как система линейных уравнений с основной матрицей, совпадающей с матрицей Якоби функции 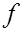в точке . Тогда, если эта матрица обратима, мы получим:

                                                                      (3)

            Выражение (3) можно рассматривать как линейную часть приращения  как функции . Но чтобы утверждать, что эта функция есть обратная к 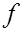и, тем более, что оператор, обратный к , есть оператор производной обратной функции в точке , нужно доказать, что линейная часть приращения (3) отличается от всего приращения обратной функции в данной точке «на бесконечно малый вектор».

            Ответ на вопрос дает следующая теорема, приводимая здесь без доказательства:

            Теорема 2.5 (теорема о производной обратной функции). Если функция  непрерывно дифференцируема в некоторой окрестности точки , и линейный оператор  обратим, то существуют такие открытые множества , содержащее точку , и , содержащее точку , что определена однозначно функция  с областью определения и областью значений так, что  и функция   непрерывно дифференцируема в точке , причем .

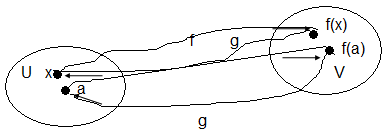
Рис. 2.10

            Итак, теорема 2.5 дает достаточные условия существования и дифференцируемости (и даже непрерывной дифференцируемости) обратной функции. Подчеркнем, что обратная функция определена локально: в некоторой окрестности точки .

            При этом оказывается, что если функция , где - область определения 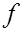, то обратная функция определена для некоторой пары открытых множеств , содержащих точки  и  соответственно, такие, что  обратим, и тогда , причем .

            Рассмотрим пример. Запишем функцию, преобразующую полярные координаты на плоскости в декартовы:

           

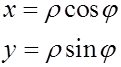
            Якобиан этой функции, как мы установили в п. 2.4, равен . Следовательно, во всех точках, кроме точки  (начало полярной системы координат), производная функции обратима. Кроме того, все частные производные непрерывны во всех точках, где они определены. Значит, условия теоремы 2.5 выполнены.

            Обратная функция

           

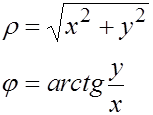
определена однозначно в любом открытом множестве , не содержащем точку , принимая значения в некотором открытом множестве, содержащемся в множестве всех таких , что . Производная обратной функции может быть вычислена и непосредственно, и через матрицу, обратную матрице Якоби исходной («прямой») функции. В последнем случае получим:

                   (4)

            Если же мы будем вычислять матрицу Якоби обратной функции непосредственно, то получим:

                                                        (5)

            Легко сообразить, что если в (4) перейти к декартовым переменным, то получится (5).    

            Рассмотрим теперь проблему дифференцируемости неявной функции.

            Пусть определена некоторая функция , и пусть в пространстве  задано множество точек, удовлетворяющих уравнению:

                                              (6)

            Поставим вопрос о существовании такой функции , что  тогда и только тогда, когда имеет место (6), т.е.  (где ).

            Например, если , , то наш вопрос в этом конкретном случае есть вопрос о существовании такой функции , что . Мы можем в данном случае указать две такие функции:

            ,

графиками которых служат верхняя и нижняя полуокружности окружности, заданной уравнением .

            В общем же случае, если указанная выше функция  существует, она называется неявной (или неявно заданной) функцией, определенной уравнением (6).

            Пусть теперь функция  дифференцируема в точке , т.е. при . Вычислим приращение функции  в этой точке, предполагая, что и сама эта точка, и точка, полученная в результате приращения аргументов, удовлетворяет уравнению (6):

                 (7)

            В (7) через  и  обозначены операторы дифференцирования по вектору  и  соответственно, т.е. матрица оператора  состоит из всех частных производных , матрица оператора  из всех частных производных , причем вторая матрица - квадратная. Мы уже сталкивались с подобным разложением матриц в первом семестре при исследовании систем линейных уравнений.

            Рассмотрим тогда (7) как векторное уравнение относительно неизвестного приращения  (приращения неявной функции, определяемой уравнением (6)). Если оператор  обратим, то мы получим:

                               (8)

            Вывод соотношения (8) (как и аналогичный вывод (3)) нельзя считать строгим доказательством того, что оператор в (8), действующий на вектор  есть производная неявной функции. Это лишь проведенные на «физическом уровне строгости» пояснения, позволяющие представить вид искомой производной.

            Достаточные условия дифференцируемости неявной функции дает следующая теорема, также формулируемая без доказательства.

            Теорема 2.6 (теорема о производной неявной функции). Если функция  непрерывно дифференцируема в некоторой окрестности точки EMBED Equation.2, и линейный оператор EMBED Equation.2 обратим, то существуют такие открытые множества EMBED Equation.2, содержащее точку EMBED Equation.2, и EMBED Equation.2, содержащее точку EMBED Equation.2, что определена однозначно функция EMBED Equation.2 с областью определения EMBED Equation.2и принимающая значения в EMBED Equation.2так, что EMBED Equation.2,  функция EMBED Equation.2 непрерывно дифференцируема в точке EMBED Equation.2, причем EMBED Equation.2

.

            Для рассмотренного выше примера (уравнение окружности) для любой внутренней точкиEMBED Equation.2 отрезка EMBED Equation.2 имее

:

            EMBED Equation.2

(в данном случае оба оператора производной оказались просто частными производными). Множество  EMBED Equatio2  в данном случае может быть выбрано как любой интервал, содержащийся в интервале , а множество - как содержащий  множество  интервал , где (если иметь в виду верхнюю полуокружность - см. рис. 2.11).

            Для сравнения продифференцируем непосредственно функцию по :

           

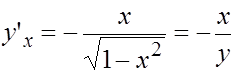
            Для функции, соответствующей нижней полуокружности, получим:

            ,

так как здесь . Заметим, что для этой неявной функции, определяемой тем же уравнением, множество  остается тем же самым, а множество  переопределяется как интервал , где . Выражение для производной, даваемое теоремой 2.6, объединяет обе возникающие здесь неявные функции (или, как иногда говорят, обе ветви многозначной функции, задаваемой уравнением вида (6) ).

                                   Рис. 2.11

            Заметим, что условия теоремы 2.6 в точках  не выполняются, так как в этих точках частная производная  обращается в ноль.

            В рассмотренном примере мы могли непосредственно из уравнения получить обе неявные функции и продифференцировать их, не прибегая к теореме 2.6. Это связано с тем, что наше уравнение позволяет аналитически (явно) выразить одну переменную через другую. Разумеется, это далеко не всегда так. Например, уравнение

                           (9)      

неразрешимо относительно любой из переменных. Но теорема 2.6 позволяет дифференцировать неявную функцию и в этом случае. Например, для функции , определяемой уравнением (9), получим производные:

           

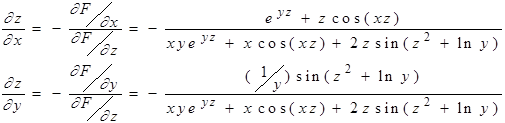
            Эти выражения, конечно, имеют смысл в точках, в которых выполняются условия теоремы 2.6.

            Следовательно, теорема о производной неявной функции позволяет дифференцировать неявную функцию даже тогда, когда она не может быть выражена аналитически через свои переменные, а может быть определена только некоторым уравнением, и получать при этом производные для всех неявных функций, которые существуют при условиях теоремы.           

            В общем случае для числовой неявной функции, т.е. при , оператор  есть обычная частная производная в точке, и мы получаем формулы для частных производных неявной функции:

            В заключение рассмотрим  простой пример «двумерной» неявной функции двух переменных, определяемой системой двух нелинейных уравнений с четырьмя «неизвестными»:

           

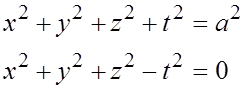
(«сечение четырехмерной сферы четырехмерным конусом»).

            Здесь

  

Определим матрицу Якоби для неявной функции .

Вычисляем матрицы:

           

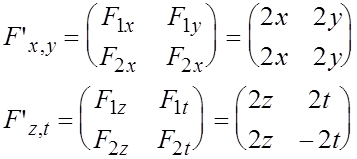
(здесь использовано  сокращенное обозначение частной производной  в виде - даже без штриха!).

Рекомендуем посмотреть лекцию "5.1 Государственная раздробленность Древней Руси".

            Детерминант второй матрицы равен  (и, следовательно, отличен от нуля во всех точках, в которых  и ).

            Далее: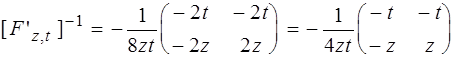

            Тогда матрица Якоби  будет равна

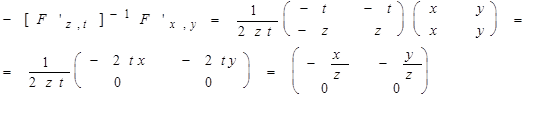
(т.е. ).

2.1.      Читателю предлагается геометрически объяснить полученный результат.