Определение элементов из L2 и его свойства

§6. Определение элементов из  и его свойства.

Поскольку элементы из  не имеют конкретного значения в отдельно взятой точке, то работа непосредственно с ними вызывает затруднения. После осреднения эти элементы обретают в каком-то смысле свойство непрерывности, что позволяет выделять из класса эквивалентности конкретный представитель − функцию.

Рассмотрим в пространстве  оператор сдвига  аргумента  .

Для функции  этот оператор определен и сохраняет норму . Поэтому он по непрерывности продолжается до линейного оператора на всем  .

Утверждение.

 при  .

Доказательство.

Пусть сначала . Тогда при  найдется шар  такой, что supp.

Функция  равномерно непрерывна в замкнутом шаре , поэтому

Рекомендуемые материалы

.

Следовательно,

.

По заданному элементу  и числу  выбираем так, чтобы .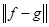

Тогда . 

Утверждение доказано.

Ядро осреднения.

Выберем  неотрицательную  четную  функцию    так,  чтобы  .  Положим  .

Тогда  .

Определение.

Осреднением элемента   называют функцию  вычисленную по формуле

.

Замечание. Осреднение определено также для элементов  так как их можно продолжить нулем на всем , получив тем самым элемент из  .

Свойства осреднения:

1  – следует из теоремы о дифференцируемости интеграла по параметру.

2   .

Доказательство.

По неравенству Коши-Буняковского

.

По выбору ядра осреднения имеем

.

Следовательно,

 .       

После замены порядка интегрирования получаем требуемое

.

3   при  .

Пусть сначала  . Тогда

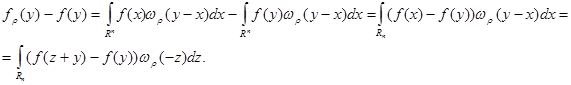
Последнее равенство получено заменой переменной  . Пользуясь четностью функции    и неравенством Коши - Буняковского будем иметь:

.

Последний интеграл равен единице, поэтому

                          .          (1)

Выбирая , добиваемся того, что интегрирование в (1) ведется по шару  что влечет неравенство .

Меняя порядок интегрирования в (1), будем иметь

     .    (2)                  

Отсюда  .

В случае произвольного элемента  выбираем   так, чтобы .

Тогда 

     .

4 Если существует обобщенная производная  ,  то  .

В самом деле,   

  .

5 Если , то  при  .

Доказательство.

Сходимость  в пространстве  эквивалентна набору сходимостей , в пространстве . Последние сходимости вытекают из свойств 3 и 4.

Информация в лекции "4.2. Н.Я. Данилевский о культурно-исторических типах" поможет Вам.

6 Если ,  то .

Доказательство.

Очевидно,    .              (3)

Поэтому     .

Далее интегрируем и меняем порядок интегрирования

       Остается воспользоваться неравенством (2) и заметить, что  .