Метод Ньютона для решения систем нелинейных уравнений

Метод Ньютона для решения систем нелинейных уравнений.

Пусть требуется решить систему нелинейных уравнений вида (7). Предположим, что решение существует в некоторой области , в которой все функции  непрерывны и имеют, по крайней мере, первую производную. Метод Ньютона представляет собой итерационный процесс, который осуществляется по определенной формуле следующего вида:

                                       (9)

где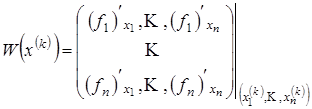

Трудности при использовании метода Ньютона:

- существует ли обратная матрица?

- не выходит ли  за пределы области ?

Модифицированный метод Ньютона облегчает первую задачу. Модификация состоит в том, что матрица вычисляется не в каждой точке, а лишь в начальной. Таким образом, модифицированный метод Ньютона имеет следующую формулу:

                                   (10)

Рекомендуемые материалы

Но ответа на второй вопрос, модифицированный метод Ньютона не дает.

Итерационный процесс по формулам (8) или (10) заканчивается, если выполняется следующее условие

.

В лекции "6.Античная проза" также много полезной информации.

Достоинством метода Ньютона является его быстрая сходимость по сравнению с методом простых итераций.

3. Решение систем линейных алгебраических уравнений.

Пусть дана система линейных алгебраических уравнений (СЛАУ) вида

                                         (11)

или в матричной форме

.                                                    (12)