Приведение нелинейного уравнения к виду, допускающему сходящиеся итерации

Приведение нелинейного уравнения  к виду , допускающему сходящиеся итерации.

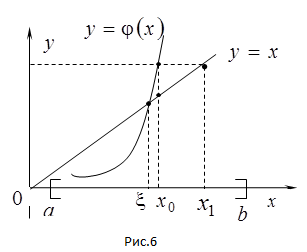
Выполнение условия сходимости можно добиться путем перехода от исходного уравнения  к эквивалентному виду  следующим образом: умножим обе части уравнения (1) на , затем прибавим к обеим частям по , тогда . Обозначим , тогда . Константа  выбирается так, чтобы выполнялось достаточное условие сходимости итерационного процесса (4), т.е. . Это условие равносильно , отсюда  при  и  при .

Требуемую точность вычислений можно обеспечить путем использования оценок приближения  к корню :

1) ; 2)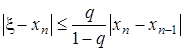

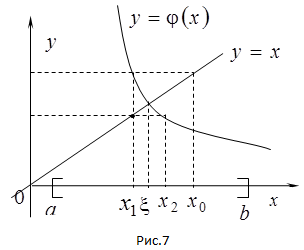
При  второе неравенство примет вид . Таким образом, если , то . Очевидно, что чем меньше , тем быстрее сходится процесс итераций. Практически грубую оценку приближенного решения можно получить без дополнительных вычислений при . В этом случае (Рис.7) итерации попеременно оказываются то с одной, то с другой стороны корня, так что корень заключен в интервале . Это надежная, хотя и грубая оценка, но она неприменима при , когда итерации сходятся к корню монотонно, т.е. с одной стороны. Вблизи корня итерации сходятся примерно так же, как геометрическая прогрессия со знаменателем . Чтобы сумма дальнейших членов прогрессии не превосходила , должен выполняться критерий сходимости

.

При выполнении этого условия процесс итераций можно прекращать. Метод простых итераций и почти все другие итерационные методы имеют два достоинства:

Рекомендуемые материалы

- являются универсальными и самоисправляющимися, то есть любая неточность на каком – либо шаге итераций не отразится на конечном результате, а лишь на количестве итераций. Подобные ошибки устойчивы даже по отношению к грубым ошибкам (сбоям ЭВМ), если только ошибка не выбрасывает очередное приближение за пределы области сходимости.

- позволяют достигнуть любой заданной точности при любом начальном приближении .

Недостатки методов:

- трудность приведения уравнения (1) к виду (2).

- если начальное приближение  далеко от корня, то число итераций достаточно большое. Объем вычислений возрастает.

Процесс итераций заканчивается при выполнении двух критериев:

1) Когда два последних приближения отличается между собой по модулю на заданную величину : . Этого критерия недостаточно, так как в случае крутизны графика, данное условие будет выполнено, но  может находиться далеко от корня.

2) Мера удовлетворения уравнению последнего приближения корня: . Отдельно второго критерия недостаточно, так как при пологой функции  условие может быть выполнено, но  может быть далеко от корня.

Ещё посмотрите лекцию "Требования к электрооборудованию" по этой теме.

Пример. Методом итераций найти корни уравнения .

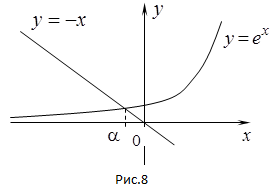
Для нахождения интервала расположения корней воспользуемся графическим методом. Для этого преобразуем исходное уравнение к виду  и построим два графика  и  (Рис.8). Абсцисса точки пересечения этих графиков является приближенным значением корня . Более точные значения можно получить по итерационной формуле (3). Из рисунка видно, что корень  находится на отрезке . Выберем ; , . На концах отрезка функция  меняет знак  на .

Запишем исходное уравнение в эквивалентном виде: , где . Выберем . Для получения корня процесс итераций  сходится, так как .

Таким образом, рабочая формула метода простых итераций будет иметь вид:

.