Ассоциативный анализ
Глава 4 Ассоциативный анализ
Ассоциативный анализ служит для выявления связей между переменными. Применительно к маркетинговым исследованиям данная группа статистических процедур позволяет ответить на вопросы типа:
■ Влияет ли на частоту посещения магазина уровень доходов покупателей?
■ Как связаны между собой пол респондентов и желание купить мотоцикл?
■ Как влияет на покупательское поведение потребителей сухих строительных смесей род занятий респондентов?
То есть при помощи ассоциативного анализа становится возможным анализировать вопросы анкеты не только по отдельности, а в зависимости от других вопросов. Этот вид анализа иногда называют построением разрезов, поскольку он позволяет определить не только наличие связи между вопросами анкеты, но и силу связи между переменными и то, каким образом ведет себя одна переменная при изменении другой (возрастает или убывает).
В процессе ассоциативного анализа выявляются следующие типы зависимостей.
■ Немонотонные зависимости свидетельствуют только о наличии определенной связи между двумя переменными, но не позволяют судить о направлении или силе связи. Пример немонотонной зависимости: мужчины в основном покупают рыбные консервы в продовольственных магазинах, а женщины — на рынках.
Рекомендуемые материалы
■ Монотонные зависимости — это зависимости, по которым можно узнать не только наличие, но и направление связи. Пример монотонной зависимости: мужчины покупают пиво чаще, чем женщины. Монотонные зависимости бывают двух видов:
возрастающие — первая переменная возрастает при возрастании второй;
убывающие — первая переменная убывает при возрастании второй.
■ Линейные зависимости характеризуются уравнением функции у = а + Ьх (график линейной функции). Связь между двумя переменными в данном случае является линейной, то есть на основании этой зависимости мы можем сказать, насколько изменится одна переменная при изменении второй.
■ Нелинейные. Примерами нелинейных связей между двумя переменными являются: экспоненциальная, логарифмическая, степенная, полиномиальная зависимости — то есть в данном случае связь присутствует и изменяется по какому-либо известному математическому закону.
Зависимости, выявленные в результате ассоциативного анализа, можно охарактеризовать тремя аспектами.
■ По наличию — определенная (систематическая) связь между двумя переменными есть.
■ По направлению — связь является убывающей или возрастающей.
■ По силе — можно определить, насколько тесно связаны между собой две переменные, то есть насколько значима данная зависимость.
Между переменными с номинальной шкалой может быть установлена только немонотонная зависимость, характеризуемая только наличием связи. Для переменных, имеющих порядковую или интервальную шкалу, данное ограничение не действует — для них можно определить и направление, и силу связи.
4.1. Перекрестные распределения и 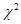
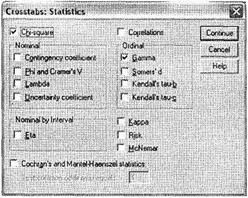
Перекрестные распределения служат для выявления различных типов зависимостей между двумя и более переменными. Например, если требуется установить, где покупают сгущенное молоко мужчины и женщины, следует воспользоваться таблицами перекрестных распределений (таблицами сопряженности, или кросста-буляции). На основании перекрестных распределений можно установить не только наличие зависимости (немонотонной или монотонной) между переменными, но, в большинстве случаев, ее тип (линейная или нелинейная) и направление (возрастающая или убывающая)1. Установленная при помощи перекрестного распределения зависимость может оказаться незначимой из-за малого размера выборки или по другим причинам. Статистическую значимость выявленной зависимости позволяет определить критерий 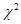 .
.
В табл. 4.1 представлены основные характеристики переменных, участвующих в анализе.
Несмотря на то что перекрестные табуляции можно строить по переменным, имеющим любой тип шкалы, необходимо иметь в виду, что большое количество категорий (вариантов ответа) анализировать трудно. Даже если анализ выявит значимую зависимость, при наличии большого числа категорий переменных исследователю будет сложно понять, каким именно образом связаны данные переменные.
Таблица 4.1. Основные характеристики переменных, участвующих в перекрестных распределениях
| Перекрестные распределения | |||
| Зависимые переменные | Независимые переменные | ||
| Количество | Тип | Количество | Тип |
| От двух до десяти | Любой | От двух до десяти | Любой |
Также следует отметить, что наибольшую эффективность кросстабуляционный анализ показывает на номинальных и порядковых переменных. Для интервальных переменных больше подходит корреляционный анализ, рассматриваемый в разделе 4.2.
И наконец, последним ограничением применения перекрестных распределений для анализа зависимостей между переменными является тот факт, что различные статистические тесты (такие как 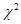 ) могут быть использованы только при анализе одновариантных переменных. Статистические тесты, применяемые для анализа зависимостей, предназначены только для двух переменных. При наличии дополнительных слоев или уровней кросстабуляционной таблицы статистический анализ производится для каждого уровня отдельно, при этом на каждом уровне он работает только с двумя переменными. Для многовариантных переменных SPSS содержит возможность отдельного построения кросстабуляции — выявить наличие и направление связи в данном случае можно только визуально.
) могут быть использованы только при анализе одновариантных переменных. Статистические тесты, применяемые для анализа зависимостей, предназначены только для двух переменных. При наличии дополнительных слоев или уровней кросстабуляционной таблицы статистический анализ производится для каждого уровня отдельно, при этом на каждом уровне он работает только с двумя переменными. Для многовариантных переменных SPSS содержит возможность отдельного построения кросстабуляции — выявить наличие и направление связи в данном случае можно только визуально.
Далее в этой главе мы покажем, как строить перекрестные распределения и анализировать зависимости для одновариантных и многовариантных переменных.
4.1.1. Перекрестные распределения для одновариантных вопросов и 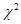
Давайте рассмотрим перекрестные распределения для одновариантных вопросов на следующем примере.
ПРИМЕР----------------------------------------------------------------------------------------------
Исходные данные:
В результате маркетингового исследования, посвященного исследованию потребительских предпочтений посетителей развлекательного центра, оказалось, что средняя частота посещения центра составляет приблизительно 12 раз в месяц. Также были получены данные о распределении среди посетителей центра мужчин и женщин различных возрастных групп. В ходе подготовительного этапа анализа были сформированы, в частности, три одновариантные переменные:
1) частота посещения центра (q25);
2) возраст респондентов (ql8);
3) пол респондентов (q23). Требуется:
1. Построить перекрестное распределение частоты посещения развлекательного центра в разрезе возраста и пола респондентов. Рассчитать среднюю частоту посещения центра различными целевыми группами потребителей.
2. Определить, влияет ли на частоту посещения центра возраст потребителей. Установить статистическую значимость зависимости между частотой посещения и возрастом.
---------------------------------------------------------------------------------------------------------------------
Из условия первой задачи следует, что мы должны построить перекрестное распределение сразу по трем переменным: q25 в зависимости от ql8 и q23 (то есть трехуровневое). Для решения задачи воспользуемся меню Analyze ► Descriptive Statistics ► Crosstabs. В открывшемся диалоговом окне (рис. 4.1) из левого списка, содержащего все доступные переменные, выберите те, которые будут расположены в строках результирующей таблицы, и те, которые будут расположены в столбцах. Поместите зависимую переменную q25 Частота посещения в область Rows (варианты ответа на вопрос о частоте посещения будут расположены в строках таблицы), а независимую переменную ql8 Возраст — в область Columns (возрастные группы будут расположены в столбцах таблицы). Осталась еще одна независимая переменная q23 Пол. Поместите ее в область Layer (уровень или слой таблицы).
Обратите внимание, что всегда, когда обратное не обусловлено задачами исследования, рекомендуется размещать переменные с малым количеством вариантов ответа в слоях. Это позволит уменьшить размерность результирующей таблицы. Мы можем задать и большее количество измерений таблицы, щелкая на кнопке Next в области Layer и добавляя релевантные переменные. Максимальное количество слоев, которое можно задать, щелкая на кнопке Next, — 8. Следовательно, максимально возможное количество измерений перекрестной таблицы по одновариантным вопросам — 10(10 = 8 слоев + 1 строковая переменная + 1 столбцовая переменная).
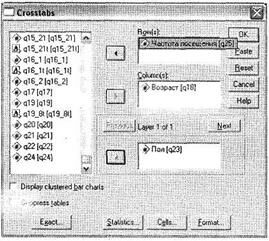 |
В диалоговом окне Crosstabs в область каждого измерения (Rows, Columns, Layer) можно поместить сразу несколько переменных. Максимальное число переменных, которые можно поместить в области Rows и Columns, — 76; для каждого из восьми возможных уровней Layer — 6. Если задано по одной переменной в строке и столбце (как в нашем случае), все дополнительно указанные слои будут отображаться в одной и той же таблице. Ситуация будет отличаться, если мы укажем несколько переменных для строк, столбцов и слоев в одних и тех же областях (не щелкая на кнопке Next для задания нескольких слоев) перекрестной таблицы. В этом случае будут построены отдельные таблицы для каждой пары строковых и столбцовых переменных.
 |
Теперь, когда вы указали все переменные для анализа, для построения перекрестных распределений можно щелкнуть на кнопке ОК. Однако сначала давайте рассмотрим некоторые другие полезные функции диалогового окна Crosstabs. Щелкните на кнопке Cells. Отрывшееся диалоговое окно Cell Display (рис. 4.2) предназначено для задания значений, выводимых в кросстабуляционной таблице. По умолчанию SPSS в каждой ячейке таблицы выводит только количество респондентов (параметр Observed). Область Percentages позволяет организовать вывод в ячейках таблицы процентов по строкам (Rows), столбцам (Columns), а также от общего числа респондентов, ответивших одновременно на все вопросы, по которым строится перекрестное распределение (Частота посещения, Возраст и Пол) (Total).
Чтобы проиллюстрировать наш пример (расчет средних частот покупки), выведем проценты по вопросу Частота посещения внутри каждой возрастной и половой группы респондентов, отметив параметр Columns и проценты по всем возрастным группам в целом (Total). Также оставим выбранный по умолчанию вывод наблюдаемых частот (Observed). После этого можно закрыть окно Cell Display, щелкнув на кнопке Continue.
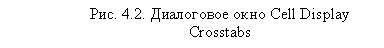 |
 |
 |
Следующее диалоговое окно, которое мы рассмотрим, — это Table Format, вызываемое при помощи кнопки Format (рис. 4.3). В нем можно выбрать тип сортировки вариантов ответа строковой переменной: возрастающая или убывающая (по алфавиту). Оставьте выбранный по умолчанию вариант Ascending (возрастающая) и щелкните на кнопке Continue, чтобы закрыть окно. После этого запустите процедуру построения перекрестных распределений, щелкнув на кнопке О К в главном диалоговом окне Crosstabs. В главном диалоговом окне процедуры есть и другие полезные (Ьункпии: мы оассмотоим их ниже.
 |
После этого в окне SPSS Viewer будет выведена требуемая таблица перекрестного распределения (рис. 4.4). В ячейках данной таблицы находятся искомые частоты
посещения развлекательного центра каждой из анализируемых целевых групп опрошенных. Например, первая ячейка показывает, что 5 (строка Count) респондентов-мужчин в возрасте от 18 до 25 лет посещают развлекательный центр каждый день. Это составляет 8,1% (подстрока % within Возраст) от общего количества мужчин в возрасте от 18 до 25 лет, ответивших на три предложенных вопроса, или 1,5% (подстрока % of Total) от общего числа мужчин, ответивших на вопросы (это число 333, оно представлено на пересечении строки и столбца Total в первой части таблицы Мужчины).
Строка Total показывает, сколько всего мужчин из каждой возрастной группы ответили на вопрос о частоте посещения центра (в нашем случае 62 респондента-мужчины в возрасте от 18 до 25 лет). Столбец Total показывает, сколько всего мужчин, посещающих развлекательный центр с различной частотой, ответили на вопрос о возрасте (в нашем случае 15 респондентов-мужчин, посещающих центр каждый день).
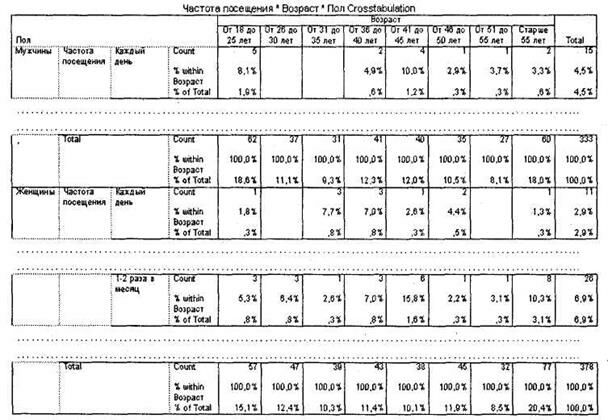 |
Вторая часть таблицы Женщины построена аналогичным образом. Как вы видите, 15,8% женщин в возрасте от 41 до 45 лет посещают развлекательный центр 1-2 раза в месяц.
 |
На основании представленной таблицы перекрестного распределения вы можете рассчитать вручную средневзвешенные частоты посещения респондентами развлекательного центра в зависимости от их пола и возраста. Для этого скопируйте анализируемую таблицу в Microsoft Excel, щелкнув на ней правой кнопкой мыши в окне SPSS Viewer и выбрав пункт Сору (не Copy Objects !). Окончательный вид полученного распределения представлен в табл. 4.2.
Таблица 4.2. Средневзвешенные частоты посещения развлекательного центра в зависимости от пола и возраста респондентов (раз в месяц)
| Пол | Возраст |
|
|
|
|
|
|
|
|
| ОТ 18 до 25 лет | От 26 до 30 лет | От 31 до 35 лет | От 36 до 40 лет | От 41 до 45 лет | От 46 до 50 лет | От 51 до 55 лет | Старше 55 |
| Мужчины | 12 | 12 | 12 | 12 | 13 | 13 | 9 | 10 |
| Женщины | 11 | 12 | 14 | 12 | 10 | 12 | 11 | 12 |
Из представленной таблицы следует, что средняя частота посещения развлекательного центра различными половозрастными группами респондентов несколько различается. Однако, исходя только из визуальных предположений, нельзя утверждать то, что частота посещения центра действительно зависит от пола и возраста. Для этого любая выявленная закономерность должна удовлетворять условию статистической значимости. Определить, значима ли выявленная нами зависимость, позволяют статистические тесты, выполняемые при построении перекрестных распределений.
Далее мы покажем, как решается второй пункт нашей задачи (условие см. выше), то есть как ответить на вопрос: «Действительно ли существует статистически значимая зависимость между тремя анализируемыми переменными или показанные в табл. 4.2 различия в частотах посещения центра вызваны влиянием случайных факторов (то есть как таковой зависимости нет)?».
Выявить статистическую значимость зависимостей между переменными позволяют критерий 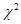 и сопутствующие тесты. Исследуем нашу зависимость между частотой посещения развлекательного центра, полом и возрастом респондентов на предмет статистической значимости. Для этого вновь откройте диалоговое окно Crosstabs. В этом окне остались две не рассмотренные нами кнопки: Exact и Statistics — именно они позволяют исследовать значимость перекрестных распределений. По умолчанию SPSS определяет статистическую значимость только на основании асимптотического метода. Одной из разновидностей данного метода и является
и сопутствующие тесты. Исследуем нашу зависимость между частотой посещения развлекательного центра, полом и возрастом респондентов на предмет статистической значимости. Для этого вновь откройте диалоговое окно Crosstabs. В этом окне остались две не рассмотренные нами кнопки: Exact и Statistics — именно они позволяют исследовать значимость перекрестных распределений. По умолчанию SPSS определяет статистическую значимость только на основании асимптотического метода. Одной из разновидностей данного метода и является 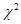 . Данный критерий используется наиболее часто в маркетинговых исследованиях. Однако применение асимптотического критерия
. Данный критерий используется наиболее часто в маркетинговых исследованиях. Однако применение асимптотического критерия 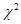 накладывает на данные, содержащиеся в анализируемой перекрестной таблице, существенные ограничения, которые подробно описаны ниже.
накладывает на данные, содержащиеся в анализируемой перекрестной таблице, существенные ограничения, которые подробно описаны ниже.
Так, важнейшим требованием к исследуемым данным является достаточно большие значения в ячейках таблицы. При наличии небольших по размеру выборок или при построении разрезов третьего и более уровня данное условие является недостижимым. Исходя из опыта анализа данных в маркетинговых исследованиях, можно утверждать, что подобные ситуации встречаются достаточно часто. В связи с этим в случае несоответствия имеющихся данных общепринятому критерию 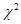 следует воспользоваться другими статистическими методами.
следует воспользоваться другими статистическими методами.
Сначала на примере перекрестного распределения по трем переменным рассмотрим использование наиболее популярного статистического метода установления статистической значимости зависимостей — критерия 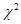 . Для того чтобы организовать наряду с перекрестной таблицей вывод соответствующих статистик, в главном диалоговом окне Crosstabs щелкните на кнопке Statistics (рис. 4.5). В открывшемся диа-
. Для того чтобы организовать наряду с перекрестной таблицей вывод соответствующих статистик, в главном диалоговом окне Crosstabs щелкните на кнопке Statistics (рис. 4.5). В открывшемся диа-
логовом окне выберите параметр Chi-square 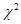 ). Это позволит впоследствии определить, имеется ли определенная связь между исследуемыми переменными.
). Это позволит впоследствии определить, имеется ли определенная связь между исследуемыми переменными.
При анализе зависимостей, кроме обнаружения наличия связи, также можно определить, насколько сильно выражена данная зависимость (установить силу связи). Сделать это позволяют релевантные статистические тесты, применяемые отдельно для каждого из трех типов переменных, участвующих в анализе. Для номинальных переменных следует применять один из тестов, представленных в области Nominal. Наиболее универсальным и часто применяемым методом является V Cramer's. Для порядковых переменных следует применять один из методов, представленных в области Ordinal. Мы рекомендуем использовать наиболее универсальный метод: Gamma. Теоретически этот же метод можно применять и для интервальных переменных, однако все же для них рекомендуется использовать более релевантную процедуру корреляционного анализа.
Далее рассмотрим, как применять перечисленные статистические методы на примере нашей задачи с двумя порядковыми переменными Частота посещения развлекательного центра и Возраст. Для этого выберите параметр Gamma и закройте описываемое окно, щелкнув на кнопке Continue. Запустите процедуру построения перекрестных распределений, щелкнув на кнопке ОК в главном диалоговом окне Crosstabs.

 |
В окне SPSS Viewer появится уже рассмотренная выше таблица перекрестного распределения трех переменных: Частота посещения, Возраст и Пол. Но, в отличие от предыдущего случая, ниже будут отображены две таблицы, из которых можно узнать о наличии, силе и направлении (только для порядковых и интервальных переменных) связи между анализируемыми переменными. Рассмотрим их по порядку.
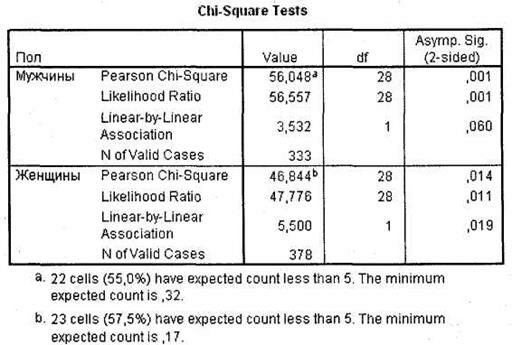
В первой таблице, Chi-Square Tests, выводятся результаты расчета критерия 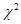 (строка Pearson Chi-Square) и некоторых других статистик (рис. 4.6). Необходимо отметить, что расчет всех статистических процедур производится для каждого варианта переменной, расположенной в слоях (в нашем случае Пол) по отдельности (то есть отдельно для целевых групп мужчин и женщин). Данное обстоятельство уже было отмечено выше.
(строка Pearson Chi-Square) и некоторых других статистик (рис. 4.6). Необходимо отметить, что расчет всех статистических процедур производится для каждого варианта переменной, расположенной в слоях (в нашем случае Пол) по отдельности (то есть отдельно для целевых групп мужчин и женщин). Данное обстоятельство уже было отмечено выше.
В нашем примере для респондентов-мужчин величина критерия 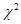 — 56,048, однако для практических целей важна не столько сама величина, столько ее значимость, представленная в столбце Asymp. Sig. (2-sided). Именно из условия статистической значимости критерия
— 56,048, однако для практических целей важна не столько сама величина, столько ее значимость, представленная в столбце Asymp. Sig. (2-sided). Именно из условия статистической значимости критерия 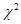 следует статистическая значимость всей зависимости. В нашем примере значимость анализируемого критерия и для мужчин, и для женщин достаточно высока (0,001 и 0,014 соответственно), что позволяет сделать предварительный вывод о том, что между частотой посещения развлекательного центра и возрастом для каждой половой группы респондентов существует определенная статистически значимая зависимость. Тем не менее одной значимости критерия
следует статистическая значимость всей зависимости. В нашем примере значимость анализируемого критерия и для мужчин, и для женщин достаточно высока (0,001 и 0,014 соответственно), что позволяет сделать предварительный вывод о том, что между частотой посещения развлекательного центра и возрастом для каждой половой группы респондентов существует определенная статистически значимая зависимость. Тем не менее одной значимости критерия 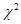 недостаточно, чтобы с уверенностью утверждать о наличии значимой зависимости между тремя анализируемыми переменными. Для этого необходимо, чтобы выполнялись следующие два критерия.
недостаточно, чтобы с уверенностью утверждать о наличии значимой зависимости между тремя анализируемыми переменными. Для этого необходимо, чтобы выполнялись следующие два критерия.
Процент ячеек, в которых ожидаемые значения1 (Expected counts) меньше или равны 5, должен быть менее или равным 20 %. Это значение отображается в примечании «а» в первой строке после таблицы Chi-Square Tests. На практике приемлемая доля ожидаемых частот меньше 5 может отклоняться от 20 % (в пределах +5 %). При наличии ярко выраженной зависимости можно считать такую зависимость статистически значимой. Также всегда необходимо иметь в виду практические соображения (и это относится ко всем без исключения статистическим процедурам). Если ожидаемые частоты меньше 5 у переменных, представляющих малую практическую значимость для исследователя, — значит, можно не принимать в расчет рассматриваемый критерий и признать зависимость значимой по практическим соображениям. Как видно на рис. 4.58, в нашем случае 55 % ячеек имеют ожидаемые значения меньше 5 (при этом минимальное ожидаемое значение 0,32). Следовательно, несмотря на то что критерий 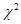 является статистически значимым, он не удовлетворяет рассматриваемому дополнительному условию.
является статистически значимым, он не удовлетворяет рассматриваемому дополнительному условию.
Суммы по строкам и столбцам должны быть больше 0. В нашем случае данное условие удовлетворяется.
Еще одной не рассмотренной статистикой в таблице Chi-Square Tests является тест Mantel-Hanzel (строка Linear-by-Lf near Association). Его значимость позволяет сделать вывод о наличии линейной зависимости между неноминальными переменными. Если величина данного теста статистически значима, следовательно, между строковой и столбцовой переменными есть линейная зависимость. В нашем случае (рис. 4.6) линейная зависимость между возрастом и частотой посещения развлекательного центра существует только в целевой группе респондентов-женщин. Про мужчин подобное сказать нельзя.
 |
После того как мы установили наличие зависимости между тремя анализируемыми переменными (при этом между возрастом и частотой посещения для респондентов-женщин существует и линейная зависимость), можно приступить к анализу таблицы Symmetric Measures (рис. 4.7), чтобы определить силу выявленной связи.
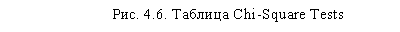 |

 |
Для порядковых переменных (как в нашем случае) определить силу связи позволяет критерий Gamma. Этот показатель может варьироваться в интервале от -1 (максимально разнонаправленная зависимость) до 1 (полная зависимость); значение О показывает полное отсутствие зависимости. Значение критерия Gamma представлено в столбце Value таблицы Symmetric Measures. В нашем случае в группе респондентов-мужчин имеется лишь весьма слабая положительная зависимость (Gamma = 0,080). Столбец Approx. Sig. свидетельствует о том, что данная зависимость еще и статистически незначима. Обратная ситуация в группе респондентов-женщин: для них установлена слабая, но статистически значимая положительная зависимость между возрастом и частотой посещения развлекательного центра.
Если в перекрестном анализе участвуют номинальные переменные, силу (но не направление) связи позволяет определить критерий Cramer's V. Отображение этого критерия можно установить в диалоговом окне Statistics при помощи параметра Phi and Cramer's V (см. рис. 4.5).
Давайте рассчитаем данный критерий для наших переменных. Результаты расчетов представлены на рис. 4.8. В целом, критерий Cramer's V может варьироваться в пределах от 0 до 1, где 0 показывает отсутствие связи между исследуемыми переменными, а 1 — полную зависимость. В нашем случае и для мужчин, и для женщин есть статистически значимые (как показывает столбец Approx. Sig.) слабые зависимости (для мужчин Cramer's V = 0,205; для женщин = 0,176). Необходимо отметить, что значение 1 для теста Cramer's V является практически недостижимым, поэтому значения 0,8-0,9 следует считать весьма высокими.
 |
 |
Итак, мы определили, что между тремя анализируемыми переменными — возрастом, полом и частотой посещения респондентами развлекательного центра — есть слабые, но статистически значимые зависимости. Вместе с тем было установлено, что больше половины (55 %) ячеек в перекрестной таблице имеют ожидаемые частоты меньше 5 — из чего следует вывод о неприменимости теста 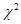 и сопутствующих асимптотических тестов (Gamma и Cramer's V) в нашем случае. В принципе мы ответили на второй пункт задачи (условие см. выше) и можем сказать, что различия, выявленные в ходе перекрестного анализа (см. табл. 4.2), действительно имеют место и являются статистически значимыми. Однако добросовестный аналитик в такой ситуации все же попытается доказать истинность сделанных выводов.
и сопутствующих асимптотических тестов (Gamma и Cramer's V) в нашем случае. В принципе мы ответили на второй пункт задачи (условие см. выше) и можем сказать, что различия, выявленные в ходе перекрестного анализа (см. табл. 4.2), действительно имеют место и являются статистически значимыми. Однако добросовестный аналитик в такой ситуации все же попытается доказать истинность сделанных выводов.
Когда анализируемые данные не удовлетворяют требованиям, предъявляемым асимптотическими методами (как, например, в нашем случае 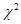 ), есть другая возможность установить статистическую значимость исследуемой зависимости. Это позволяют сделать точные (Exact) тесты.
), есть другая возможность установить статистическую значимость исследуемой зависимости. Это позволяют сделать точные (Exact) тесты.
Откройте главное диалоговое окно перекрестного анализа Crosstabs (см. рис. 4.1), щелкнув на кнопке Exact. В появившемся диалоговом окне Exact Tests (рис. 4.9) по умолчанию установлен расчет только асимптотических критериев. Данное диалоговое окно позволяет провести расчеты по двум неасимптотическим методам: Monte-Carlo и Exact, причем последний метод не рекомендуется использовать в практических целях, так как он занимает много времени. Для практических целей следует применять метод Monte-Carlo с установленным по умолчанию количеством выборок (10 000). Доверительный уровень 99 % практически всегда является слишком высоким, поэтому измените его на 95 %, что соответствует доверительному уровню при расчете статистической ошибки выборки для маркетинговых исследований (см. раздел 1.2). Все остальные параметры диалогового окна Crosstabs аналогичны указанным в предыдущем примере. Теперь можно запустить процедуру построения перекрестных распределений.
 |
 |
После завершения всех необходимых расчетов в окне SPSS Viewer будут выведены результаты. Их структура аналогична рассмотренной выше, за исключением того, что таблицы Chi-Square Tests и Symmetric Measures расширены за счет результатов теста Monte-Carlo. Единственным практическим результатом данного теста является рассчитанная статистическая значимость критериев, указанных в диалоговом окне Statistics (см. рис. 4.5).
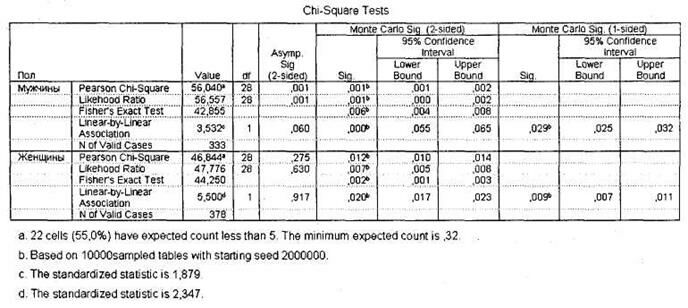
На рис. 4.10 представлена таблица Chi-Square Tests с результатами теста Monte-Carlo. Искомые значения статистической значимости представлены в столбце Monte Carlo Sig. (2-sided) в подстолбце Sig.. В подстолбцах Lower Bound и Upper Bound показаны, соответственно, нижний и верхний пределы, в которых варьируется значение статистической значимости Sig.. Так, в нашем случае критерий 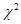 действительно свидетельствует о наличии статистически значимой зависимости между полом, возрастом и частотой посещения развлекательного центра — это следует из весьма высокой значимости теста Monte-Carlo (0,001 — для мужчин и 0,012 — для женщин). В 95 % случаев данное значение не выходит за рамки статистической значимости (например, для мужчин оно варьируется в пределах от 0,001 до 0,002). Также из таблицы мы видим, что выявленная связь является линейной только для целевой группы респондентов-женщин. Таким образом, для нашего случая все предварительные выводы, сделанные нами в таблице Chi-Square Tests, подтвердились результатами теста Monte-Carlo.
действительно свидетельствует о наличии статистически значимой зависимости между полом, возрастом и частотой посещения развлекательного центра — это следует из весьма высокой значимости теста Monte-Carlo (0,001 — для мужчин и 0,012 — для женщин). В 95 % случаев данное значение не выходит за рамки статистической значимости (например, для мужчин оно варьируется в пределах от 0,001 до 0,002). Также из таблицы мы видим, что выявленная связь является линейной только для целевой группы респондентов-женщин. Таким образом, для нашего случая все предварительные выводы, сделанные нами в таблице Chi-Square Tests, подтвердились результатами теста Monte-Carlo.
 |
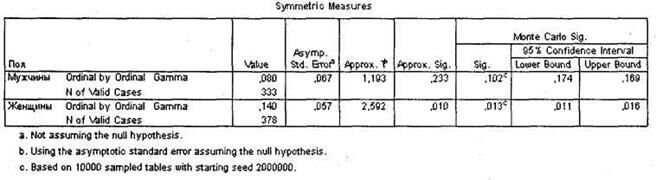
Теперь рассмотрим таблицу Symmetric Measures (рис. 4.11), на основании которой мы сделали выводы о силе выявленной зависимости. Результаты теста Monte-Carlo и в данном случае подтверждают выводы асимптотического метода: между частотой посещения центра и возрастом в целевой группе респондентов-женщин выявлена слабая статистически значимая зависимость. Для мужчин зависимость статистически незначима.
 |
Таким образом, мы выяснили, что между частотой посещения развлекательного центра и возрастом респондентов-женщин существует статистически значимая зависимость, характеризующаяся слабой положительной линейностью. Для респондентов-мужчин возраст и частота посещения центра также связаны статистически значимой зависимостью, однако сделать точный вывод о характере данной зависимости не представляется возможным.
Вернемся к табл. 4.2 и покажем, как интерпретировать представленные в ней данные. На основании проведенных расчетов можно утверждать, что мужчины в возрасте старше 51 года посещают развлекательный центр реже всего (примерно 2 раза в неделю). Наиболее частыми посетителями развлекательного центра являются мужчины в возрасте младше 50 лет (примерно 3 раза в месяц). В целевой группе женщин можно выделить три группы. Наиболее частыми посетителями являются женщины в возрасте 31-35 лет (примерно 4 раза в неделю). Среднюю группу (примерно 3 раза в неделю) составляют женщины младше 30 лет, от 36 до 40 лет и старше 46 лет. И наконец, группу респондентов-женщин, посещающих центр реже всего, составляет возрастная группа от 41 до 45 лет.
4.1.2. Перекрестные распределения для многовариантных вопросов
Как уже было сказано выше (см. раздел 3.2), все статистические процедуры применимы только для одновариантных вопросов. На практике установить статистическую зависимость в многовариантных вопросах можно только двумя способами.
■ Визуально. В этом случае аналитик должен самостоятельно (на основании опыта или опираясь на другие данные, выявленные в ходе исследования) попытаться сделать заключение о значимости различий между двумя переменными. Например, если мужчины покупают сметану в упаковке в 4 раза чаще, чем женщины, и при этом число респондентов, ответивших на данный вопрос, достаточно велико (скажем, 100 человек), можно сделать вывод о статистической значимости данного различия.
■ Можно рассматривать многовариантный вопрос как несколько дихотомических переменных с вариантами ответа «есть/нет» и строить по ним стандартные перекрестные распределения (при помощи процедуры Crosstabs). На практике в подавляющем большинстве случаев именно данный способ является оптимальным. Тем не менее необходимо отметить, что дихотомические переменные, являющиеся вариантами ответа на многовариантный вопрос, могут принимать участие даже в корреляционном анализе в качестве порядковых переменных (см. раздел 4.2).
Кроме существенных ограничений при установлении статистических зависимостей между многовариантными переменными, их анализ осложнен также и тем, что результаты перекрестных распределений по многовариантным вопросам SPSS выводит только в виде простого текста (plain text)1.
Ниже мы проиллюстрируем процесс построения перекрестных распределений по многовариантным переменным на примере двух многовариантных вопросов из маркетингового исследования московского рынка сметаны. Первый вопрос Где Вы покупаете сметану? (q7) с вариантами ответа:
■ продмаг (q7_l);
■ рынок (q7_2);
■ супермаркет (q7_3);
■ палатка (q7_4);
■ универсам (q7_5).
Второй вопрос Какую сметану Вы предпочитаете? с вариантами ответа:
■ в упаковке (ql6_l);
■ развесную (ql6_2).
Как было сказано выше в разделе 2.2.2, чтобы строить распределения (линейные или перекрестные) по многовариантным переменным, сначала их нужно сформировать. Мы не будем возвращаться к процедуре создания многовариантных переменных при помощи меню Analyze ► Multiple Response ► Define Sets; этот процесс описан в разделе 2.2.2. Давайте исходить из того, что вы самостоятельно сформировали две многовариантные переменные, назовем их q7 (Место покупки сметаны) и ql6 (Наиболее предпочтительная для респондентов упаковка сметаны). Теперь можно заняться построением перекрестного распределения по этим вопросам, то есть ответить на вопрос: «Зависят ли предпочтения респондентов в отношении сметаны (упакованной или развесной) от места совершения покупки?».
Построение перекрестного распределения по многовариантным вопросам осуществляется при помощи меню Analyze ► Multiple Response ► Crosstabs. В открывшемся диалоговом окне (рис. 4.12) слева вы видите два списка переменных. В верхнем находятся все доступные переменные из файла данных (включая и дихотомические переменные — варианты ответа на анализируемые многовариантные вопросы). Нижний список содержит только сформированные нами многовариантные переменные ($q7 и $ql6). В перекрестном анализе могут принимать участие как
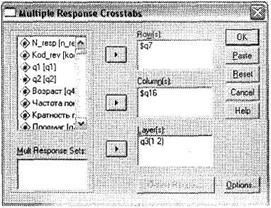 |
многовариантные переменные, так и другие доступные одновариантные переменные. Как для кросстабуляций (см. раздел 4.1.1), для перекрестных таблиц можно задать несколько измерений (максимум три) при помощи введения одного дополнительного слоя (область Layer). Имейте в виду, что при построении перекрестных таблиц, переменные, находящиеся в областях Row(s), Column(s) и Layer(s), перекрещиваются по тройкам последовательно.
 |
Итак, поместите в область Row(s) переменную Место покупки сметаны (q7), а в область Column(s) — переменную Предпочтения сметаны (ql6). В область Layer(s) поместите переменную Пол (q3).
Как вы поняли, мы будем рассматривать трехмерное перекрестное распределение. Обратите внимание на то, что при внесении в одну из трех областей переменной из верхнего левого списка (всех доступных переменных в базе данных) после имени этой переменной появляется строка символов вида (? ?) и становится доступной кнопка Define Ranges. Это подсказывает нам, что следует ввести границы изменения одновариантной переменной. Выделите переменную q3 в поле Layer(s) и щелкните на кнопке Define Ranges.
 |
На экране появится новое диалоговое окно Define Variable Ranges (рис. 4.13). В нем в соответствующих полях следует указать минимальное Minimum и максимальное Maximum значения, которые может принимать данная переменная. В нашем случае пол респондентов может быть либо мужским (код 1), либо женским (код 2). Поэтому введите 1 в качестве минимального значения, а 2 — в качестве максимального и щелкните на кнопке Continue для того, чтобы закрыть это диалоговое окно.
 |
Необходимо отметить, что переменные, участвующие в рассматриваемом статистическом анализе, для которых указываются интервалы допустимых значений, должны принимать только целые значения (дробные SPSS будет игнорировать). Это связано с ограничением при использовании в кросстабуляциях по многовариантным вопросам переменных с интервальной шкалой. Такие переменные могут использоваться, только если они принимают целые значения.
Щелкните на кнопке Options. Открывшееся диалоговое окно (рис. 4.14) позволяет указать, нужно ли выводить проценты (по строкам — Row, по столбцам — Column или общие — Total), а также определить, что является базой для расчета процентов: количество респондентов (Cases) или количество ответов на вопрос (Responses)1.
 |
 |
Давайте выведем проценты по строкам (то есть доли респондентов, предпочитающих разный вид сметаны в каждом из пяти рассматриваемых типов торговых точек). Оставьте выбранный по умолчанию параметр Cases в области Percentages Based on — это позволит вам рассчитать проценты от общего числа респондентов (гистограмма), а не от количества ответов на вопрос (сектограмма). Щелкните на кнопке Continue для того, чтобы закрыть диалоговое окно, и запустите процедуру построения перекрестного распределения при помощи щелчка на кнопке О К в главном диалоговом окне программы.
В окне SPSS Viewer будет выведена перекрестная таблица с результатами расчетов. Обратите внимание, что таблица разбита на две части: первая содержит результаты построения перекрестного распределения предпочтений сметаны и места покупки для мужчин (рис. 4.15), а вторая — для женщин (рис. 4.16). Таким образом, можно сказать, что собственно построения перекрестного распределения по трем заданным переменным (включая переменную Пол) не происходит.
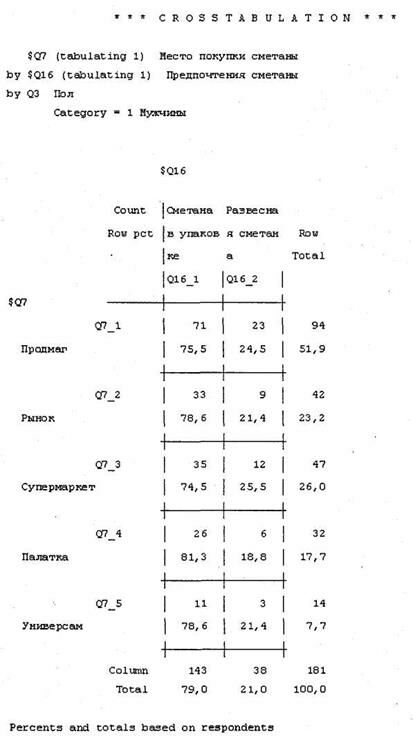 |
Переменная, указанная в качестве слоя (Layer), не отображается в таблице. Вместо этого ее значение (для каждого из вариантов ответа, в нашем случае — мужчины и женщины) отображается в верхней части каждой кросстабуляции как текст Category = 1 Мужчины (для мужчин) и Category = 2 Женщины (для женщин).
 |

 |
В нижней части под всеми таблицами расположены две строки, содержащие информацию об общих параметрах построения перекрестных распределений. Так, в нашем случае мы видим, что все проценты, представленные в таблицах, рассчитаны от общего числа респондентов (Percents and totals based on respondents). Во второй строке отражаются:
■ количество результативных анкет (то есть анкет, в которых респонденты ответили на три вопроса) — 940 valid cases;
■ количество анкет, не включенных в анализ (респонденты не дали ответа хотя бы на один из трех вопросов), — 63 missing cases.
Общий размер выборки равен сумме результативных и исключенных анкет: 1003 = 940 + 63. В таблицах приведены результаты построения перекрестного распределения предпочтений респондентов по типу сметаны в зависимости от места покупки. Необходимо отметить, что проценты в ячейках таблицы отражают доли покупателей, предпочитающих сметану в упаковке и развесную для каждого из рассматриваемых мест покупки. Например, 75,5 % мужчин, покупающих сметану в продовольственных магазинах, предпочитают сметану в упаковке, а 24,5 % — развесную1.
Проценты в строке Column Total отражают доли респондентов, предпочитающих сметану в упаковке или развесную, от общего числа респондентов (в нашем случае мужского или женского пола), ответивших на рассматриваемые вопросы. Например, 79 % мужчин, ответивших на рассматриваемые вопросы, предпочитают упакованную сметану, а 21 % — развесную.
Проценты в столбце Row Total отражают доли респондентов, покупающих сметану в различных торговых точках. На рис. 4.15 вы видите, что 51,9 % мужчин, ответивших на рассматриваемые вопросы, покупают сметану в продовольственных магазинах. Значения на пересечении строки Column Total и столбца Row Total показывают общее количество респондентов мужского пола, ответивших на вопросы о предпочтениях сметаны и месте покупки (как и всегда, в абсолютных и относительных величинах). В нашем случае на рассматриваемые вопросы ответил 181 мужчина. Обратите внимание, что длинные таблицы, выводимые в виде текста, могут по умолчанию не отражаться полностью в окне SPSS Viewer. Чтобы убедиться, что вы видите таблицу целиком, дважды щелкните мышью на ней. Откроется специальная область с возможностью прокрутки, в которой вы можете увидеть все построенные таблицы.
4.2. Корреляционный анализ
Корреляционный анализ предназначен для выявления наличия, а также определения направления и силы линейной связи между несколькими переменными, имеющими интервальный или порядковый тип шкалы. Необходимо отметить, что дихотомические переменные также могут принимать участие в корреляционном анализе. С точки зрения SPSS они рассматриваются как порядковые переменные.
В табл. 4.3 представлены основные характеристики переменных, участвующих в анализе.
Таблица 4.3. Основные характеристики переменных, участвующих в корреляционном анализе
| Корреляционный анализ | |||
| Зависимые переменные | Независимые переменные | ||
| Количество | Тип | Количество | Тип |
| _ | _ | Любое | Интервальная |
| Порядковая | |||
| Дихотомическая |
Наличие, направление и силу линейной связи отражают коэффициенты корреляции. Они варьируются от -1 до +1.
■ -1 соответствует абсолютно разнонаправленной зависимости (с возрастанием одной переменной другая убывает);
■ +1 отражает полное соответствие между переменными (то есть они, по сути, являются одним и тем же);
■ 0 показывает полное отсутствие всякой связи.
Для удобства интерпретации корреляций применяются семантические интервалы, причем при анализе данных в маркетинговых исследованиях обычно используются следующие градации (табл. 4.4).
Таблица 4.4. Градации коэффициентов корреляции
| Значение коэффициента корреляции | Характеристика силы линейной связи |
| От ±0,81 до ±1,00 | Сильная |
| От ±0,61 до ±0,80 | Умеренная (средняя) |
| От ±0,41 до ±0,60 | Слабая |
| От ±0,21 до ±0,40 | Очень слабая |
| От ±0,00 до ±0,20 | Нет корреляции |
Существует два основных типа коэффициентов корреляции, рассчитываемых в зависимости от вида шкалы переменных, участвующих в анализе.
1. Для переменных с интервальной шкалой применяется коэффициент корреляции Пирсона. Он позволяет охарактеризовать линейную связь между двумя переменными по указанным параметрам (табл. 4.4): наличию (есть/нет), направлению (убывает/возрастает) и силе (очень слабая/слабая/умеренная/сильная).
2. Если хотя бы одна из пары исследуемых переменных имеет порядковую или дихотомическую шкалу, используются ранговые коэффициенты корреляции Спирмана или Кендала. Чаще всего эти коэффициенты применяются в маркетинговых исследованиях в тех случаях, когда необходимо установить степень соответствия двух ранжированных списков. Например, если имеются схемы выбора какого-либо продукта различными целевыми группами респондентов (в виде ранжированных по важности параметров) и необходимо установить, насколько точно они соответствуют друг другу (или различаются).
Ниже мы рассмотрим перечисленные типы коэффициентов корреляции более подробно на практических примерах из маркетинговых исследований.
4.2.1. Исследование линейных корреляций по Пирсону, Спирману и Кендалу
Сначала мы рассмотрим пример применения коэффициента корреляции Пирсона. Предположим, что у нас есть ответы респондентов на следующие два вопроса. Каков Ваш среднемесячный доход в расчете на одного члена семьи? с вариантами ответа:
■ до $100;
■ от $ 100 до $ 300;
■ от $ 300 до $ 600;
■ от $ 600 до $ 1000;
■ от $ 1000 до $ 1500;
■ свыше $1500.
Как часто Вы посещаете рестораны? с вариантами ответа:
■ более 1 раза в день;
■ примерно 1 раз в день;
■ 2-3 раза в неделю;
■ примерно 1 раз в неделю;
■ 2-3 раза в месяц;
■ примерно 1 раз в месяц;
■ реже 1 раза в месяц.
В результате ввода в компьютер заполненных анкет респондентов были получены две переменные: q3 (первый вопрос) и q28 (второй вопрос). Необходимо установить, зависит ли частота посещения ресторанов от дохода респондентов, и если да, то каким образом. В связи с тем, что в ходе опроса при ответе на каждый вопрос респондентам предлагалось на выбор несколько вариантов ответа, тип шкалы у полученных переменных получился порядковым (в файле данных есть только коды ответов, но не сами числовые значения, отражающие частоту посещения ресторана или уровень дохода).
Далее мы рассмотрим не только как использовать коэффициент корреляции Пирсона, но также как использовать данный коэффициент для анализа квазипорядковых переменных. Дело в том, что некоторые переменные, хотя они и закодированы как порядковые, по сути являются интервальными (как в нашем случае). Это делается специально, чтобы, с одной стороны, увеличить долю респондентов, ответивших на вопрос, а с другой стороны, уменьшить число возможных ошибок при вводе в компьютер текстовых полей (для открытых вопросов). Интервалы также полезны при анализе, поскольку нет необходимости кодировать текстовые (или интервальные) переменные, а можно сразу увидеть группы (интервалы) значений. Практика показывает, что подобное составление анкет для маркетинговых исследований является стандартным, поэтому корреляционный анализ редко проводится на изначально интервальных переменных (текстовые поля анкеты).
Для описываемых квазипорядковых переменных следует применять именно коэффициент корреляции Пирсона. Использование коэффициентов Спирмана или Кендала в этом случае является некорректным. Более подробно эти два коэффициента представлены ниже; пока же в общих чертах о них можно сказать следующее. Коэффициенты Спирмана или Кендала показывают только степень соответствия порядка следования вариантов ответа в ранжированных списках (есть отсутствие инверсий). При этом корреляции по Спирману и Кендалу используются в основном, когда элементы ранжированных списков представлены мнемоническими, а не числовыми константами. Таким образом, данные коэффициенты не помогут нам в характеристике зависимости между частотой посещения ресторанов и доходом респондентов. Однако в нашем случае нельзя применять и коэффициент корреляции Пирсона, так как в этом случае анализировались бы коды интервалов (1 -6 — в первом вопросе и 1 -7 — во втором), а не действительные ответы респондентов на вопросы1.
Итак, сначала мы должны преобразовать имеющиеся у нас порядковые переменные к интервальному виду. Лучше всего сделать это при помощи замены кодов интервалов (1-6) на средние значения данных интервалов. Например, среднее значение для интервала 3 в переменной q3 — это $ 450 (450 = (300 + 600) / 2). Преобразовав обе переменные к данному виду, мы получим следующие интервальные переменные q3_i и q28_i (табл. 4.5)2.
Таблица 4.5. Схема перекодировки порядковых переменных (q3 и q28) в интервальные (q3_i и q28_i)
| Порядковые переменные | Интервальные переменные |
| Каков Ваш среднемесячный доход в расчете на одного члена семьи? | |
| до $ 100 | $50 |
| от $ 100 до $ 300 | $200 |
| от $ 300 до $ 600 | $450 |
| от $ 600 до $ 1000 | $ 800 |
| от $ 1000 до $ 1500 | $ 1250 |
| свыше $ 1500 | $ 1750 |
| Как часто Вы посещаете рестораны? | |
| более 1 раза в день | 60 раз в месяц |
| примерно 1 раз в день | 30 раз в месяц |
| 2-3 раза в неделю | 10 раз в месяц |
| примерно 1 раз в неделю | 4 раза в месяц |
| 2-3 раза в месяц | 2,5 раза в месяц |
| примерно 1 раз в месяц | 1 раз в месяц |
| реже 1 раза в месяц | 0,5 раза в месяц |
 |
Теперь мы можем приступить непосредственно к корреляционному анализу (описанию зависимости между частотой посещения ресторанов и уровнем дохода). Для этого выберите пункт меню Analyze ► Correlate ► Bivariate. В открывшемся диалоговом окне (рис. 4.17) выберите в левом списке всех доступных переменных две интересующие нас (q3_i и q28_i) и перенесите их в область Variables. Остальные параметры в этом диалоговом окне, установленные по умолчанию, следует оставить неизменными: вывод коэффициентов корреляции Пирсона (параметр Pearson в области Correlation Coefficients) и статистической значимости коэффициентов (параметр Two-tailed в области Test of Significance). Кнопка Options не предлагает исследователю каких-либо существенных параметров. Чтобы запустить процедуру построения корреляционной таблицы, щелкните на кнопке ОК.
 |
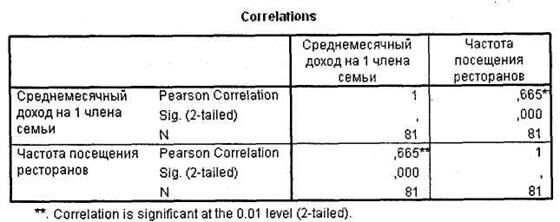
В окне SPSS Viewer появится таблица Correlations с результатами расчетов коэффициента корреляции Пирсона и статистической значимости данного коэффициента. Как видно из рис. 4.18, в нашем случае коэффициент корреляции Пирсона между двумя исследуемыми переменными (q3_i и q28_i) равен +0,665, а его статистическая значимость меньше 0,001. Следовательно, можно сделать вывод о том, что между среднемесячным доходом респондентов и частотой посещения ими ресторанов существует статистически значимая умеренная (средняя) линейная возрастающая зависимость. То есть частота посещения ресторанов в достаточно высокой степени (коэффициент Пирсона = 0,7) зависит от уровня доходов потребителей, причем при росте среднемесячного дохода частота посещения ресторанов линейно возрастает.
Существует возможность проводить корреляционный анализ сразу для нескольких переменных. Для этого необходимо поместить эти переменные в область Variables диалогового окна Bivariate Correlations. В таблице Correlations будут показаны коэффициенты корреляции для каждой пары исследуемых переменных.
Теперь рассмотрим процедуру проведения корреляционного анализа при помощи ранговых коэффициентов Спирмана и Кендала. В данных методах одна переменная (эталонная) представлена в виде ранжированной последовательности мнемонических категорий, а другой переменной присваиваются ранговые места. Корреляционные коэффициенты рассчитываются исходя из количества инверсий, то есть числа нарушений порядка следования рангов по сравнению с первым рядом. В большинстве случаев рекомендуется применять коэффициент корреляции Спирмана. Использование коэффициента Кендала оправдано только в том случае, когда в структуре данных имеются выбросы.
 |
В практике маркетинговых исследований наиболее часто коэффициенты корреляции Спирмана применяются для анализа не всей выборочной совокупности респондентов (базы данных в целом), а агрегированных ранжированных перечней, полученных в результате других преобразований1. Приведем пример. Предположим, что в результате опроса посетителей магазинов одежды были получены ответы на следующие два вопроса. Какие факторы для Вас наиболее важны при выборе одежды? с вариантами ответа:
■ Высокое качество одежды.
■ Доступные цены.
■ Широта ассортимента одежды.
■ Близость к дому или работе.
■ Высокое качество обслуживания.
■ Красивый интерьер магазина.
Оцените, пожалуйста, следующие характеристики данного магазина одежды (в котором происходит опрос) по пятибалльной шкале (от 1 — очень плохо до 5 — отлично) с вариантами ответа:
■ Высокое качество одежды.
■ Доступные цены.
■ Широта ассортимента одежды.
■ Близость к дому или работе.
■ Высокое качество обслуживания.
■ Красивый интерьер магазина.
■ Ваша общая оценка работы данного магазина.
Над результатами второго вопроса был проведен множественный линейный регрессионный анализ. Анализировалось влияние оценок частных параметров всех исследованных магазинов одежды на их общую оценку. В разделе 4.3 подробно рассматривается процедура линейного регрессионного анализа, позволяющая, в частности, построить ранжированный перечень частных параметров по силе их влияния на общую оценку.
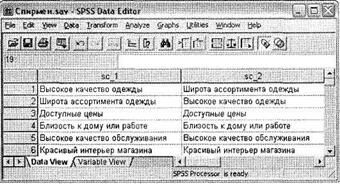
Таким образом, были получены два ранжированных списка с одинаковыми категориями: две схемы выбора магазина одежды. Затем оба списка были введены в SPSS под кодами, представленными выше: от 1 (наиболее важный фактор) до 6 (наименее важный фактор) (рис. 4.19). На рис. 4.20 представлены данные списки в мнемонической форме. Первый список представлен в переменной sc_l; второй — в sc_2.

 |
 |
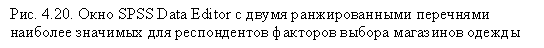 |
Как вы видите на рис. 4.20, две схемы выбора, составленные на основании прямого метода (вопрос 1) и на основании регрессионного анализа (вопрос 2), соответствуют друг другу не полностью, различаясь в порядке следования первой и второй категорий. Проанализируем эти схемы выбора магазинов одежды на предмет соответствия при помощи коэффициента корреляции Спирмана.
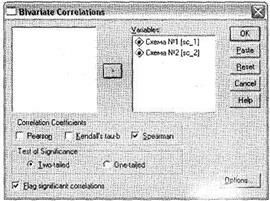 |
Для этого снова откройте диалоговое окно Bi variate Correlations, выбрав пункт меню Analyze ► Correlate ► Bivariate. Перенесите две интересующие нас переменные — Схема №1 (составленная по вопросу 1) и Схема №2 (составленная по вопросу 2) — из левого списка всех доступных переменных в область Variables (рис. 4.21). Отмените вывод корреляции Пирсона и вместо него выберите параметр Spearman (корреляция Спирмана). После этого начните расчет при помощи щелчка на кнопке ОК.
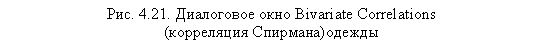 |
 |
В окне SPSS Viewer появится таблица Correlations с результатами расчета коэффициента ранговой корреляции (Спирмана) по двум анализируемым переменным. Как следует из рис. 4.22, две рассматриваемые схемы выбора различаются несущественно. Данный вывод можно сделать из сильной корреляции между переменными sc_l и sc_2 (коэффициент корреляции Спирмана = 0,9), характеризующейся весьма высокой статистической значимостью (0,005).
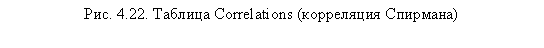 |
В заключение напомним, что ранговый коэффициент корреляции Спирмана (в отличие от Кендала) может применяться и в качестве аналога корреляции Пирсона при исследовании зависимостей между переменными, не приводимыми к интервальному виду и потому не являющимися ранжированными списками. В качестве примера можно привести гипотетический случай, рассмотренный выше, когда анализируется влияние пола респондентов (дихотомическая шкала) на уровень образования (порядковая по сути, но номинальная по виду шкала).
4.2.2. Частные корреляции. Выявление ложных корреляций
На практике иногда возникают ситуации, когда в результате корреляционного анализа обнаруживаются логически необъяснимые, противоречащие объективному опыту исследователя корреляции между двумя переменными (например, оказывается, что между уровнем дохода респондентов и количеством детей в семье существует статистически значимая зависимость). В этом случае говорят о так называемой ложной корреляции, исследовать которую помогают частные коэффициенты корреляции.
Рассмотрим процедуру исследования частных корреляций на следующем примере из маркетингового исследования поведения посетителей залов игровых автоматов. В результате обработки анкет респондентов были, в частности, получены три интервальные переменные:
■ q47 — возраст;
■ q49 — количество членов семьи;
■ q50 — среднемесячный доход на 1 члена семьи.
Над данными переменными был проведен корреляционный анализ (Пирсона), который выявил логически необъяснимую, но статистически значимую зависимость между переменными: Доход и Количество членов семьи (рис. 4.23).

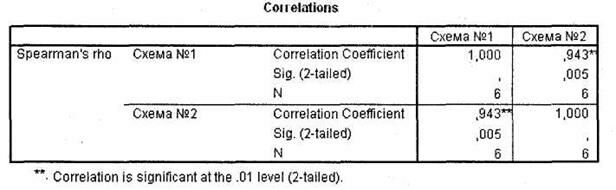 |
Как видно из таблицы, обе рассматриваемые переменные коррелируют с третьей переменной Возраст. В такой ситуации корреляция между уровнем дохода респондентов и численностью их семей может объясняться влиянием третьей переменной: возраста респондентов. То есть связанными (коррелирующими), на самом деле, являются пары возраст/уровень дохода и возраст/количество членов семьи. Проверим данную гипотезу при помощи частных коэффициентов корреляции.
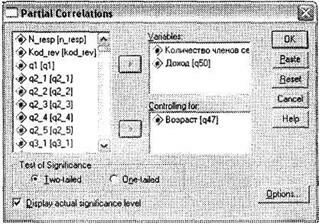 |
Откройте диалоговое окно Partial Correlations (меню Analyze ► Correlate ► Partial). В левом списке всех доступных переменных выберите переменные, между которыми обнаружена странная корреляция (q50 Доход и q49 Количество членов семьи), и поместите их в область Variables. Переменную, с которой коррелируют обе исследуемые переменные (q47 Возраст), поместите в область Controlling for (рис. 4.24). В этом диалоговом окне больше ничего не изменяйте — просто запустите программу на исполнение, щелкнув на кнопке ОК.
 |
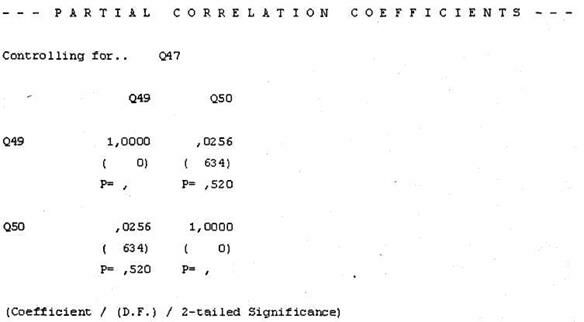
В окне SPSS Viewer появятся результаты расчетов частных коэффициентов корреляции (рис. 4.25). В данной таблице первая строка каждой ячейки содержит коэффициент корреляции Пирсона, а третья — статистическую значимость данного коэффициента. Из таблицы вы видите, что между количеством членов семьи (q49) и уровнем дохода (q50) больше не наблюдается статистически значимой корреляции (Р = 0,520), а коэффициент Пирсона сильно уменьшился (0,0256). Следовательно, корреляция, представленная на рис. 4.23, объясняется влиянием третьей переменной Возраст и, таким образом, является ложной.
 |
 |
4.3. Линейный регрессионный анализ и статистическое
прогнозирование
Линейная регрессия является наиболее часто используемым видом регрессионного анализа. Ниже перечислены три основные задачи, решаемые в маркетинговых исследованиях при помощи линейного регрессионного анализа.
1. Определение того, какие частные параметры продукта оказывают влияние на общее впечатление потребителей от данного продукта. Установление направления и силы данного влияния. Расчет, каким будет значение результирующего параметра при тех или иных значениях частных параметров. Например, требуется установить, как влияет возраст респондента и его среднемесячный доход на частоту покупок глазированных сырков.
2. Выявление того, какие частные характеристики продукта влияют на общее впечатление потребителей от данного продукта (построение схемы выбора продукта потребителями). Установление соотношения между различными частными параметрами по силе и направлению влияния на общее впечатление. Например, имеются оценки респондентами двух характеристик мебели производителя X — цены и качества, — а также общая оценка мебели данного производителя. Требуется установить, какой из двух параметров является наиболее значимым для покупателей при выборе производителя мебели и в каком конкретном соотношении находится значимость для покупателей данных двух факторов (параметр Цена в х раз более значим для покупателей при выборе мебели, чем параметр Качество).
3. Графическое прогнозирование поведения одной переменной в зависимости от изменения другой (используется только для двух переменных). Как правило, целью проведения регрессионного анализа в данном случае является не столько расчет уравнения, сколько построение тренда (то есть аппроксимирующей кривой, графически показывающей зависимость между переменными). По полученному уравнению можно предсказать, каким будет значение одной переменной при изменении (увеличении или уменьшении) другой. Например, требуется установить характер зависимости между долей респондентов, осведомленных о различных марках глазированных сырков, и долей респондентов, покупающих данные марки. Также требуется рассчитать, насколько возрастет доля покупателей сырков марки х при увеличении потребительской осведомленности на 10 % (в результате проведения рекламной кампании).
В зависимости от типа решаемой задачи выбирается вид линейного регрессионного анализа. В большинстве случаев (1 и 2) применяется множественная линейная регрессия, в которой исследуется влияние нескольких независимых переменных на одну зависимую. В случае 3 применима только простая линейная регрессия, в которой участвуют только одна независимая и одна зависимая переменные. Это связано с тем, что основным результатом анализа в случае 3 является линия тренда, которая может быть логически интерпретирована только в двухмерном пространстве. В общем случае результатом проведения регрессионного анализа является построение уравнения регрессии вида: у = а + Ь,х, + Ь2х2 + ... + Ь„хп, позволяющего рассчитать значение зависимой переменной при различных значениях независимых переменных.
В табл. 4.6 представлены основные характеристики переменных, участвующих в анализе.
Таблица 4.6. Основные характеристики переменных, участвующих в линейном регрессионном анализе
| Линейная регрессия | |||
| Зависимые переменные | Независимые переменные | ||
| Количество | Тип | Количество | Тип |
| Одна | Интервальная | Любое | Интервальная |
| Порядковая | Порядковая | ||
| Дихотомическая |
В связи с тем что и множественная и простая регрессии строятся в SPSS одинаковым способом, рассмотрим общий случай множественной линейной регрессии как наиболее полно раскрывающий суть описываемого статистического метода. Давайте рассмотрим, как построить линию тренда с целью статистического прогнозирования.
Исходные данные:
В ходе опроса респондентов, летающих одним из трех классов (первым, бизнес- или эконом-классом), просили оценить по пятибалльной шкале — от 1 (очень плохо) до 5 (отлично) — следующие характеристики сервиса на борту самолетов авиакомпании X: комфортабельность салона, работа бортпроводников, питание во время полета, цена билетов, спиртные напитки, дорожные наборы, аудиопрограммы, видеопрограммы и пресса. Также респондентам предлагалось поставить общую (итоговую) оценку обслуживания на борту самолетов данной авиакомпании.
Для каждого класса полета требуется:
1) Выявить наиболее значимые для респондентов параметры обслуживания на борту.
2) Установить, какое влияние оказывают оценки частных параметров обслуживания на борту на общее впечатление авиапассажиров от полета.
Откройте диалоговое окно Linear Regression при помощи меню Analyze ► Regression ► Linear. Из левого списка выберите зависимую переменную для анализа. Это будет Общая оценка сервиса на борту. Поместите ее в область Dependent. Далее в левом списке выберите независимые переменные для анализа: частные параметры сервиса на борту — и поместите их в область Independent(s).
Существует несколько методов проведения регрессионного анализа: enter, stepwise, forward и backward. He вдаваясь в статистические тонкости, проведем регрессионный анализ посредством пошагового метода backward как наиболее универсального и релевантного для всех примеров из маркетинговых исследований.
Так как задача анализа содержит требование провести регрессионный анализ в разрезе трех классов полета, выберите в левом списке переменную, обозначающую класс (q5) и перенесите ее в область Selection Variable. Затем щелкните на кнопке Rule, чтобы задать конкретное значение данной переменной для регрессионного анализа. Следует отметить, что за одну итерацию можно построить регрессию только в разрезе какого-то одного класса полета. В дальнейшем следует повторить все этапы сначала по количеству классов (3), каждый раз выбирая следующий класс.
Если нет необходимости проводить регрессионный анализ в каком-либо разрезе, оставьте поле Selection Variable пустым.
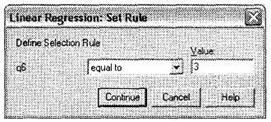
Итак, на экране открылось диалоговое окно Set Rule, в котором вы должны указать, для какого именно класса полета вы хотите построить регрессионную модель. Выберите экономический класс, закодированный как 3 (рис. 4.26).
 |
 |
В более сложных случаях, когда требуется построить регрессионную модель в разрезе трех и более переменных, следует воспользоваться условным отбором данных (см. раздел 1.5.1). Например, если кроме класса полета есть еще и необходимость раздельного построения регрессионной модели для респондентов (мужчин и женщин), необходимо перед открытием диалогового окна Linear Regression произвести условный отбор анкет респондентов, являющихся мужчинами. Далее проводится регрессионный анализ по описываемой схеме. Для построения регрессии для женщин следует повторить все этапы сначала: вначале выбрать только анкеты респондентов-женщин и затем уже для них построить регрессионную модель.
Щелкните на кнопке Continue в диалоговом окне Set Rule — вы вновь вернетесь к основному диалоговому окну Linear Regression. Последним шагом перед запуском процедуры построения регрессионной модели является выбор пункта Collinearity Diagnostics в диалоговом окне, появляющемся при щелчке на кнопке Statistics (рис. 4.27). Установление требования провести диагностику наличия коллинеарности между независимыми переменными позволяет избежать эффекта мульти-коллинеарности, при котором несколько независимых переменных могут иметь настолько сильную корреляцию, что в регрессионной модели обозначают, в принципе, одно и то же (это неприемлемо).
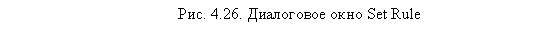 |
 |
Теперь основное диалоговое окно Linear Regression примет вид, показанный на рис. 4.28. Щелчок на кнопке О К приведет к запуску процедуры построения линейной регрессии.
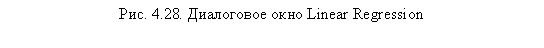 |
 |
Рассмотрим основные элементы отчета о построении регрессионной модели (окно SPSS Viewer), содержащие наиболее значимые для исследователя данные. Необходимо отметить, что все таблицы, представленные в отчете Output, содержат несколько блоков, соответствующих количеству шагов SPSS при построении модели. На каждом шаге при используемом методе backward из полного списка независимых переменных, введенных в модель изначально, при помощи наименьших частных коэффициентов корреляции последовательно исключаются переменные — до тех пор, пока соответствующий коэффициент регрессии не оказывается незначимым (Sig > 0,05). В нашем примере таблицы состоят из трех блоков (регрессия строилась в три шага). При интерпретации результатов регрессионного анализа следует обращать внимание только на последний блок (в нашем случае 3).
Первое, на что следует обратить внимание, — это таблица ANOVA (рис. 4.29). На третьем шаге статистическая значимость (столбец Sig) должна быть меньше или равна 0,05.
Затем следует рассмотреть таблицу Model Summary, содержащую важные сведения о построенной модели (рис. 4.30). Коэффициент детерминации R является характеристикой силы общей линейной связи между переменными в регрессионной модели. Он показывает, насколько хорошо выбранные независимые переменные способны определять поведение зависимой переменной. Чем выше коэффициент детерминации (изменяющийся в пределах от 0 до 1), тем лучше выбранные независимые переменные подходят для определения поведения зависимой переменной. Требования к коэффициенту R такие же, как к коэффициенту корреляции (см. табл. 4.4): в общем случае он должен превышать хотя бы 0,5. В нашем примере R = 0,66, что является приемлемым показателем.
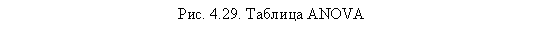 |
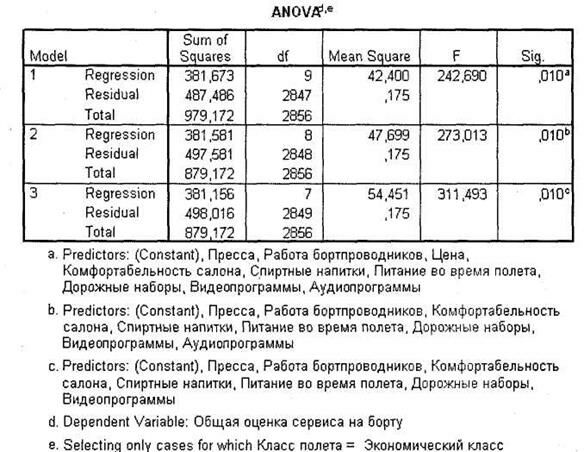 |
Также важной характеристикой регрессионной модели является коэффициент R2, показывающий, какая доля совокупной вариации в зависимой переменной описывается выбранным набором независимых переменных. Величина R2 изменяется от 0 до 1. Как правило, данный показатель должен превышать 0,5 (чем он выше, тем показательнее построенная регрессионная модель). В нашем примере R2 =■ 0,43 — это значит, что регрессионной моделью описано только 43 % случаев (дисперсии в итоговой оценке полета). Таким образом, при интерпретации результатов регрессионного анализа следует постоянно иметь в виду существенное ограничение: построенная модель справедлива только для 43 % случаев.
Третьим практически значимым показателем, определяющим качество регрессионной модели, является величина стандартной ошибки расчетов (столбец Std. Error of the Estimate). Данный показатель варьируется в пределах от 0 до 1. Чем он меньше, тем надежнее модель (в общем случае показатель должен быть меньше 0,5). В нашем примере ошибка составляет 0,42, что является завышенным, но в целом приемлемым результатом.
На основании таблиц AN OVA и Model Summary можно судить о практической пригодности построенной регрессионной модели. Учитывая, что AN OVA показывает весьма высокую значимость (менее 0,001), коэффициент детерминации превышает 0,6, а стандартная ошибка расчетов меньше 0,5, можно сделать вывод о том, что с учетом ограничения модель описывает 43 % совокупной дисперсии, то есть построенная регрессионная модель является статистически значимой и практически приемлемой.

 |
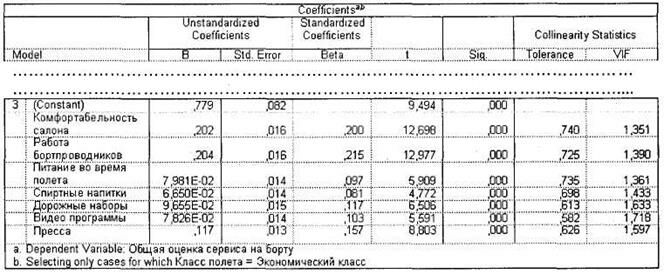
После того как мы констатировали приемлемый уровень качества регрессионной модели, можно приступать к интерпретации ее результатов. Основные практические результаты регрессии содержатся в таблице Coefficients (рис. 4.31). Под таблицей вы можете видеть, какая переменная была зависимой (общая оценка сервиса на борту) и для какого класса полета происходило построение регрессионной модели (эконом-класс). В таблице Coefficients практически значимыми являются четыре показателя: VIF, Beta, В и Std. Error. Рассмотрим последовательно, как их следует интерпретировать.
 |
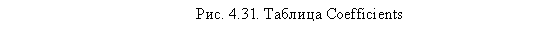 |
Прежде всего необходимо исключить возможность возникновения ситуации мультиколлинеарности (см. выше), при которой несколько переменных могут обозначать почти одно и то же. Для этого необходимо посмотреть на значение VIF возле каждой независимой переменной. Если величина данного показателя меньше 10 — значит, эффекта мультиколлинеарности не наблюдается и регрессионная модель приемлема для дальнейшей интерпретации. Чем выше этот показатель, тем более связаны между собой переменные. Если какая-либо переменная превышает значение в 10 VIF, следует пересчитать регрессию без этой независимой переменной. В данном примере автоматически уменьшится величина R2 и возрастет величина свободного члена (константы), однако, несмотря на это, новая регрессионная модель будет более практически приемлема, чем первая.
В первом столбце таблицы Coefficients содержатся независимые переменные, составляющие регрессионное уравнение (удовлетворяющие требованию статистической значимости). В нашем случае в регрессионную модель входят все частные характеристики сервиса на борту самолета, кроме аудиопрограмм. Исключенные переменные содержатся в таблице Excluded Variables (здесь не приводится). Итак, мы можем сделать первый вывод о том, что на общее впечатление авиапассажиров от полета оказывают влияние семь параметров: комфортабельность салона, работа бортпроводников, питание во время полета, спиртные напитки, дорожные наборы, видеопрограммы и пресса.
После того, как мы определили состав параметров, формирующих итоговое впечатление от полета, можно определить направление и силу влияния на него каждого частного параметра. Это позволяет сделать столбец Beta, содержащий стандартизированные  - коэффициенты регрессии. Данные коэффициенты также дают возможность сравнить силу влияния параметров между собой. Знак (+ или -) перед
- коэффициенты регрессии. Данные коэффициенты также дают возможность сравнить силу влияния параметров между собой. Знак (+ или -) перед  -коэффициентом показывает направление связи между независимой и зависимой переменными. Положительные
-коэффициентом показывает направление связи между независимой и зависимой переменными. Положительные  -коэффициенты свидетельствуют о том, что возрастание величины данного частного параметра увеличивает зависимую переменную (в нашем случае все независимые переменные ведут себя подобным образом). Отрицательные коэффициенты означают, что при возрастании данного частного параметра общая оценка снижается. Как правило, при определении связи между оценками параметров это свидетельствует об ошибке и означает, например, что выборка слишком мала.
-коэффициенты свидетельствуют о том, что возрастание величины данного частного параметра увеличивает зависимую переменную (в нашем случае все независимые переменные ведут себя подобным образом). Отрицательные коэффициенты означают, что при возрастании данного частного параметра общая оценка снижается. Как правило, при определении связи между оценками параметров это свидетельствует об ошибке и означает, например, что выборка слишком мала.
Например, если бы перед  - коэффициентом параметра работы бортпроводников стоял знак -, его следовало бы интерпретировать следующим образом: чем хуже работают бортпроводники, тем лучше становится общее впечатление пассажиров от полета. Такая интерпретация является бессмысленной и не отражающей реального положения вещей, то есть ложной. В таком случае лучше пересчитать регрессию без данного параметра; тогда доля вариации в итоговой оценке, описываемой исключенным параметром, будет отнесена на счет константы (увеличивая ее). Соответственно уменьшится и процент совокупной дисперсии, описываемой регрессионной моделью (величина R2). Однако это позволит восстановить семантическую релевантность.
- коэффициентом параметра работы бортпроводников стоял знак -, его следовало бы интерпретировать следующим образом: чем хуже работают бортпроводники, тем лучше становится общее впечатление пассажиров от полета. Такая интерпретация является бессмысленной и не отражающей реального положения вещей, то есть ложной. В таком случае лучше пересчитать регрессию без данного параметра; тогда доля вариации в итоговой оценке, описываемой исключенным параметром, будет отнесена на счет константы (увеличивая ее). Соответственно уменьшится и процент совокупной дисперсии, описываемой регрессионной моделью (величина R2). Однако это позволит восстановить семантическую релевантность.
Еще раз подчеркнем, что сделанное замечание справедливо для нашего случая (оценки параметров). Отрицательные  - коэффициенты могут быть верными и отражать семантические реалии в других случаях. Например, когда уменьшение дохода респондентов приводит к увеличению частоты покупок дешевых товаров. В таблице вы видите, что в наибольшей степени на общее впечатление пассажиров от полета влияют два параметра: работа бортпроводников и комфортабельность салона (
- коэффициенты могут быть верными и отражать семантические реалии в других случаях. Например, когда уменьшение дохода респондентов приводит к увеличению частоты покупок дешевых товаров. В таблице вы видите, что в наибольшей степени на общее впечатление пассажиров от полета влияют два параметра: работа бортпроводников и комфортабельность салона ( - коэффициенты по 0,21). Напротив, в наименьшей степени формирование итоговой оценки сервиса на борту происходит за счет впечатления от обслуживания спиртными напитками (0,08). При этом два первых параметра оказывают почти в три раза более сильное влияние на итоговую оценку полета, чем
- коэффициенты по 0,21). Напротив, в наименьшей степени формирование итоговой оценки сервиса на борту происходит за счет впечатления от обслуживания спиртными напитками (0,08). При этом два первых параметра оказывают почти в три раза более сильное влияние на итоговую оценку полета, чем
спиртные напитки. На основании стандартизированных (3-коэффициентов регрессии можно построить рейтинг влияния частных параметров сервиса на борту на общее впечатление авиапассажиров от полета, разделив их на три группы по силе влияния:
■ наиболее значимые параметры;
■ параметры, имеющие среднюю значимость;
■ параметры, имеющие низкую значимость для респондентов (рис. 4.32).
В крайнем правом столбце содержатся  - коэффициенты, умноженные на 100, — для облегчения сравнения параметров между собой.
- коэффициенты, умноженные на 100, — для облегчения сравнения параметров между собой.
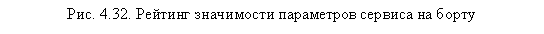
Данный рейтинг также можно интерпретировать и как рейтинг значимости для респондентов различных параметров сервиса на борту (в общем случае — схема выбора). Так, наиболее важными факторами являются первые два (1-2); среднюю значимость для пассажиров имеют следующие три параметра (3-5); относительно малое значение имеют последние два фактора (6-7).
Регрессионный анализ позволяет выявить истинные, глубинные мотивы респондентов при формировании общего впечатления о каком-либо продукте. Как показывает практика, такого уровня приближения нельзя достичь обычными методами — например, просто спросив респондентов: Какие факторы из нижеперечисленных оказывают наибольшее влияние на Ваше общее впечатление от полета самолетами нашей авиакомпании?. Кроме того, регрессионный анализ позволяет достаточно точно оценить, насколько один параметр более-менее значим для респондентов, чем другой, и на этом основании классифицировать параметры на критические, имеющие среднюю значимость и малозначимые.
Столбец В таблицы Coefficients содержит коэффициенты регрессии (нестандарти-зированные). Они служат для формирования собственно регрессионного уравнения, по которому можно рассчитать величину зависимой переменной при разных значениях независимых.
Особая строка Constant содержит важную информацию о полученной регрессионной модели: значение зависимой переменной при нулевых значениях независимых переменных. Чем выше значение константы, тем хуже подходит выбранный перечень независимых переменных для описания поведения зависимой переменной. В общем случае считается, что константа не должна быть наибольшим коэффициентом в регрессионном уравнении (коэффициент хотя бы при одной переменой должен быть больше константы). Однако в практике маркетинговых исследований часто свободный член оказывается больше всех коэффициентов вместе взятых. Это связано в основном с относительно малыми размерами выборок, с которыми приходится работать маркетологам, а также с неаккуратным заполнением анкет (некоторые респонденты могут не поставить оценку каким-либо параметрам). В нашем случае величина константы меньше 1, что является весьма хорошим результатом.
Итак, в результате построения регрессионной модели можно сформировать следующее регрессионное уравнение:
СБ = 0,78 + 0,20К + 0.20Б + 0,08ПП + 0.07С + 0Д0Н + 0,08В + 0Д2П, где
■ СБ — общая оценка сервиса на борту;
■ К — комфортабельность салона;
■ Б — работа бортпроводников;
■ ПП — питание во время полета;
■ С — спиртные напитки;
■ Н — дорожные наборы;
■ В — видеопрограмма;
■ П — пресса.
Последний показатель, на который целесообразно обращать внимание при интерпретации результатов регрессионного анализа, — это стандартная ошибка, рассчитываемая для каждого коэффициента в регрессионном уравнении (столбец Std. Error). При 95%-ном доверительном уровне каждый коэффициент может отклоняться от величины В на ±2 х Std.Error. Это означает, что, например, коэффициент при параметре Комфортабельность салона (равный 0,202) в 95 % случаев может отклоняться от данного значения на ±2 х 0,016 или на ±0,032. Минимальное значение коэффициента будет равно 0,202 - 0,032 = 0,17; а максимальное - 0,202 + 0,032 = 0,234. Таким образом, в 95 % случаев коэффициент при параметре «комфортабельность салона» варьируется в пределах от 0,17 до 0,234 (при среднем значении 0,202). На этом интерпретация результатов регрессионного анализа может считаться завершенной. В нашем случае следует повторить все шаги еще раз: сначала для бизнес -, потом для эконом-класса.
Теперь давайте рассмотрим другой случай, когда необходимо графически представить зависимость между двумя переменными (одной зависимой и одной независимой) при помощи регрессионного анализа. Например, если мы примем итоговую оценку полета авиакомпанией X в 2001 г. за зависимую переменную S,, а тот же показатель в 2000 г. — за независимую переменную So, то для построения уравнения тренда (или регрессионного уравнения) нужно будет определить параметры соотношения S, = а + b x So. Построив данное уравнение, также можно построить регрессионную прямую и, зная исходную итоговую оценку полета, спрогнозировать величину данного параметра на следующий год.
Эту операцию следует начать с построения регрессионного уравнения. Для этого повторите все вышеописанные шаги для двух переменных: зависимой Итоговая оценка 2001 и независимой Итоговая оценка 2000. Вы получите коэффициенты, при помощи которых можно в дальнейшем строить линию тренда (как в SPSS, так и любыми другими средствами). В нашем случае полученное регрессионное уравнение имеет вид: S{ = 0,18 + 0,81 х So. Теперь построим уравнение линии тренда в SPSS.
 |
Диалоговое окно Linear Regression имеет встроенное средство для построения графиков — кнопку Plots. Однако это средство, к сожалению, не позволяет на одном графике построить две переменные: S, и So- Для того чтобы построить тренд, необходимо использовать меню Graphs ► Scatter. На экране появится диалоговое окно Scatterplot (рис. 4.32), которое служит для выбора типа диаграммы. Выберите вид Simple. Максимально возможное число независимых переменных, которое можно изобразить графически, — 2. Поэтому при необходимости графического построения зависимости одной переменной (зависимой) от двух независимых (например, если бы в нашем распоряжении были данные не по двум, а по трем годам), в окне Scatterplot следует выбрать 3-D. Схема построения трехмерной диаграммы рассеяния не имеет существенных отличий от описываемого способа построения двухмерной диаграммы.
 |
После щелчка на кнопке Define на экране появится новое диалоговое окно, представленное на рис. 4.34. Поместите в поле Y Axis зависимую переменную (Итоговая оценка 2001), а в поле X Axis — независимую (Итоговая оценка 2000). Щелкните на кнопке 0 К, что приведет к построению диаграммы рассеяния.
Для того чтобы построить линию тренда, дважды щелкните мышью на полученной диаграмме; откроется окно SPSS Chart Editor. В этом окне выберите пункт меню Chart ► Options; далее пункт Total в области Fit Line; щелкните на кнопке Fit Options. Откроется диалоговое окно Fit Line, выберите в нем тип аппроксимирующей линии (в нашем случае Linear regression) и пункт Display R-square in legend. После закрытия окна SPSS Chart Editor в окне SPSS Viewer появится линейный тренд, аппроксимирующий наши наблюдения по методу наименьших квадратов. Также на диаграмме будет отражаться величина R2, которая, как было сказано выше, обозначает долю совокупной вариации, описываемой данной моделью (рис. 4.35). В нашем примере она равна 53 %.
 |
С линейным регрессионным анализом связано множество интегральных показателей, рассчитываемых на основании коэффициентов регрессии (чаще всего стандартизированных). В качестве примера приведем расчет коэффициента потребительской привлекательности продукта/марки (Consumer Attractiveness), или коэффициента СА.
 |
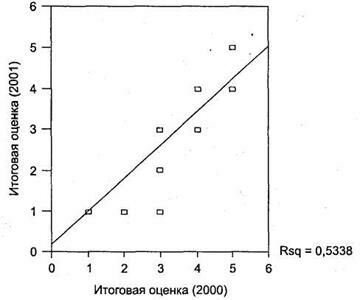 |
 |
Этот коэффициент вводится в маркетинговых исследованиях для удобства сравнения привлекательности для респондентов анализируемых продуктов/марок. В анкете должны присутствовать вопросы типа Оцените представленные параметры продукта/ марки X, в которых респондентам предлагается дать свои оценки частным параметрам продукта или марки X, скажем, по пятибалльной шкале (от 1 — очень плохо до 5 — отлично). В конце списка оцениваемых частных параметров респонденты должны поставить итоговую оценку продукту/марке X. При анализе полученных в ходе опроса ответов респондентов на основании оценок респондентов формируются:
■ матрица средневзвешенных оценок по параметрам продукта/марки;
■ список стандартизированных  - коэффициентов регрессии (оценка влияния частных параметров продукта/марки X на его/ее общую оценку).
- коэффициентов регрессии (оценка влияния частных параметров продукта/марки X на его/ее общую оценку).
Далее коэффициент СА рассчитывается по следующей формуле:
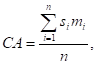
где n — число параметров, формирующих итоговую оценку продукта или марки:
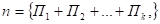
 - — значимость для респондентов параметра с индексом i (стандартизированный
- — значимость для респондентов параметра с индексом i (стандартизированный  -коэффициент регрессии, оценивающей влияние частных параметров на общую оценку продукта/марки, подробнее см. выше);
-коэффициент регрессии, оценивающей влияние частных параметров на общую оценку продукта/марки, подробнее см. выше);  — уровень средневзвешенной оценки продукта/марки по параметру с индексом i (при наличии пятибалльной шкалы):
— уровень средневзвешенной оценки продукта/марки по параметру с индексом i (при наличии пятибалльной шкалы):
 = 2 при высоком уровне оценки (средневзвешенный балл ≥ 4,5)
= 2 при высоком уровне оценки (средневзвешенный балл ≥ 4,5)
Бесплатная лекция: "21 Лечение сифилиса" также доступна.
 = 1 при среднем уровне оценки (средневзвешенный балл ≥4,0 и < 4,5)
= 1 при среднем уровне оценки (средневзвешенный балл ≥4,0 и < 4,5)
 = -1 при низком уровне оценки (средневзвешенный балл ≥3,0 и < 4,0)
= -1 при низком уровне оценки (средневзвешенный балл ≥3,0 и < 4,0)
 = -2 при неудовлетворительной оценке (средневзвешенный балл < 3,0)
= -2 при неудовлетворительной оценке (средневзвешенный балл < 3,0)
Рассчитанный для каждого конкурирующего продукта/марки коэффициент СА показывает его/ее относительную позицию в структуре потребительских предпочтений. Данный интегральный показатель учитывает уровень оценок по каждому параметру, скорректированный на их значимость. При этом он может изменяться в пределах от -1 (наихудшая относительная позиция среди всех рассматриваемых продуктов/марок) до 1 (наилучшее положение); 0 означает, что данный продукт/ марка ничем особенным не выделяется в глазах респондентов.
Итогом расчета коэффициента СА является рейтинг конкурентов по данному показателю. На основании рейтинга можно сделать важные выводы относительно лидерства и аутсайдерства конкретных продуктов/марок на потребительском рынке.
Мы завершаем рассмотрение ассоциативного анализа. Данная группа статистических методов применяется в отечественных компаниях в настоящее время достаточно широко (особенно это касается перекрестных распределений). Вместе с тем хотелось бы подчеркнуть, что только лишь перекрестными распределениями ассоциативные методы не ограничиваются. Для проведения действительно глубокого анализа следует расширить спектр применяемых методик за счет методов, описанных в настоящей главе.























