Основы моделирования социально-экономических систем
ТЕМА 1. Основы моделирования социально-экономических систем
1.1. Экономико-математические методы и их классификация
Экономико-математические методы (ЭММ) – это комплекс экономических и математических научных дисциплин, объединенных для изучения социально-экономических систем и процессов. Таким образом, объектом исследования (предметом) ЭММ являются социально-экономические системы.
Под социально-экономическими системами (СЭС) понимают такие системы, в которых рассматриваются экономические, социальные, организационные или управленческие процессы. Любая система обладает свойством целостности, т.е. ее свойства не сводятся к сумме свойств составляющих ее элементов. Таким образом, социально-экономическая система обладает такими свойствами, которых нет у каждого из ее элементов. Кроме того, можно выделить также следующие особенности СЭС, которые позволяют отнести их к классу сложных систем и затрудняют задачу их исследования:
1) Процессы в этих системах являются динамическими, т.е. изменяются во времени.
2) Элементами системы являются люди, поведение которых трудно формализуемо.
3) На систему в значительной мере влияют внешние факторы. Поэтому экономическую систему трудно изолировать от окружающей среды и исследовать ее в чистом виде.
4) События в системе чаще всего носят случайный характер, и некоторые параметры системы не определены.
5) Количество переменных, которые описывают систему, очень велико.
Рекомендуемые материалы
6) Массовый характер экономических явлений и процессов. Выявление закономерностей требует большого числа наблюдений.
Целью исследования социально-экономических систем является решение следующих практических задач:
1) анализ экономических объектов и процессов;
2) экономическое прогнозирование, т.е. предвидение развития экономических процессов;
3) выработка оптимальных управленческих решений на всех уровнях хозяйственной иерархии.
Для сравнения управленческих решений необходимо ввести понятие критерия оптимальности. Критерий оптимальности – это экономический показатель, на основании которого осуществляется выбор лучшего управленческого решения. Критерии оптимальности бывают натуральные и стоимостные, максимизируемые и минимизируемые. Например, максимизируемые критерии: валовая, конечная, чистая продукция, прибыль, рентабельность. Минимизируемые критерии: себестоимость, общие затраты и т.д. В моделях критерий оптимальности формализуется в виде целевой функции.
Классификация экономико-математических методов сводится к классификации научных дисциплин, входящих в их состав. Поскольку ЭММ является сплавом экономики, математики и информационных технологий, в ее составе можно выделить следующие разделы:
1) Экономическая кибернетика (наука об управлении экономикой). Выделяют такие разделы, как теория экономической информации, теория управляющих систем.
2) Математическая экономика. Для нее характерен системный подход, т.е. экономика рассматривается как совокупность ее функциональных подсистем (производственной, финансово-кредитной, потребительской) Основные разделы – теория производственных функций, теория спроса и потребления, межотраслевые балансы. Основной математический аппарат – линейное программирование.
3) Эконометрия. Это наука, которая на базе реальных статистических данных позволяет найти доказательство или опровержение того или иного экономического закона или гипотезы. Основной аппарат – математическая статистика. Одно из важнейших направлений эконометрии – это анализ временных рядов и построение прогнозов.
4) Исследование операций в экономике. Методы исследования операций дают обоснование выбора оптимальной стратегии с учетом конкретной обстановки Основные разделы:
- математическое программирование
- теория игр
- сетевое планирование и управление
5) Другие методы и модели анализа экономики:
- теория массового обслуживания изучает системы, в которых происходит массовое удовлетворение запросов на какие- либо услуги;
- имитационное моделирование позволяет построить на ЭВМ алгоритмическую модель некоторого экономического процесса и производить на ней эксперименты;
- методы экспертных оценок используются для построения моделей в тех случаях, когда необходимо учесть опыт специалистов в некоторой области (экспертов).
1.2.Основные понятия моделирования
Основным методом исследования социально-экономических систем является метод моделирования. Моделированием называется способ изучения реального объекта через рассмотрение подобного ему и более простого объекта, т.е. его модели. Таким образом, моделирование предполагает разработку модели, исследование этой модели и перенос результатов исследования на реальный объект.
Модель – это образ реального объекта, отражающий существенные свойства этого объекта и замещающий его в ходе исследования. Модель может быть материальной (образец, макет) или идеальной (описание, схема, график и т.д.).
Математической моделью называется формализованное на языке математики описание объекта или процессов, в нем протекающих. Математические модели имеют вид функций, уравнений, неравенств и их систем.
Сложность СЭС делает невозможным создание полной модели, учитывающей все без исключения факторы. Поэтому модель отображает лишь некоторые, существенные черты исходного объекта и замещает оригинал в строго ограниченном смысле. В зависимости от целей моделирования один и тот же объект может иметь различные модели. Под адекватностью модели понимается ее соответствие исследуемым чертам и свойствам исходного объекта. Критерием адекватности является совпадение результатов моделирования и результатов эксперимента на реальном объекте.
Классификация экономико- математических моделей.
Единой системы классификации моделей не существует. Имеются несколько признаков классификации. Рассмотрим некоторые из них.
1. По общему целевому назначению различают теоретико-аналитические модели, используемые при изучении общих свойств и закономерностей экономических процессов, и прикладные модели, применяемые в решении конкретных экономических задач анализа, прогнозирования и управления.
2. По степени агрегирования объектов моделирования модели подразделяются на макроэкономические и микроэкономические. Макроэкономические модели отражают функционирование экономики как единого целого, а микроэкономические модели связаны, как правило, с такими звеньями экономики, как предприятия и фирмы.
3. По учету фактора времени выделяют статические модели, в которых все зависимости отнесены к одному моменту времени, и динамические модели, описывающие экономические системы в развитии.
4. По учету фактора неопределенности модели подразделяются на детерминированные и стохастические. Детерминированными называются модели объектов, состояние которых однозначно определяется через параметры, входную информацию и начальные условия. Если же состояние объекта зависит также и от некоторых случайных величин, то модель является стохастической.
5. По типу математического аппарата, используемого в модели, различают следующие виды моделей:
· Математического программирования;
· Сетевого планирования и управления;
· Массового обслуживания;
· Теории игр;
· Корреляционно-регрессионные модели;
· И т.д.
1.3. Комплексный анализ работы торговых и промышленных объектов как пример простейшей модели
Пусть имеется m торговых или промышленных объектов, деятельность которых необходимо оценить с точки зрения эффективности их работы. Деятельность каждого из них характеризуется значениями n экономических показателей X1, X2,… Xn. Например, имеется пять райпотребсоюзов (m=5), по каждому из которых имеются данные о товарообороте (X1), охвате доходов населения (X2), уровне издержек (X3) и оборачиваемости капитала (X4), т.е. всего n=4 показателя (см.табл. 1.1).
Таблица 1.1. Показатели работы пяти РПС
| РПС, номер | Показатели | |||
| X1, млн. руб | X2, % | X3, % | X4, дней | |
| 1 | 740 | 60 | 5 | 70 |
| 2 | 500 | 75 | 6,5 | 50 |
| 3 | 800 | 75 | 6 | 90 |
| 4 | 620 | 90 | 7 | 60 |
| 5 | 600 | 70 | 4 | 75 |
Оценить деятельность торговых объектов сразу по всем показателям сложно: по товарообороту лучше всех работает один объект, по уровню издержек – другой, и т.д. Поэтому для такой оценки используют следующий прием: рассчитывают комплексные суммарные показатели работы каждого торгового объекта Qi, которые учитывают влияние всех данных показателей. Считается, что наиболее эффективно работает тот торговый объект, у которого суммарный комплексный показатель наибольший.
Однако, чтобы рассчитать комплексный суммарный показатель, нельзя просто просуммировать значения всех натуральных показателей, ибо они имеют различный экономический смысл и свои единицы измерения (например, товарооборот- млн. руб.; оборачиваемость – дни и т.д.). Поэтому от каждого натурального показателя Xj (j=1,…,n) переходят к безразмерному показателю Yj (j=1,…,n). Данный показатель не имеет единиц измерения и принимает значения от 0 до 1. Для перехода к безразмерному показателю используется одна из формул:
Yij=(Xij–Аj)/(Вj–Аj), (1.1)
Yij=(Вj–Xij)/(Вj–Аj). (1.2)
Здесь i- номер объекта, j – номер показателя, Аj–минимальное и Вj–максимальное значения для любого j-го показателя среди всех i объектов:

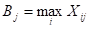
Формула (1.1) выбирается для перехода от Xj к безразмерному показателю Yj, когда по экономическому смыслу “чем больше Xj, тем лучше”, а формула (1.2)–когда “чем меньше Xj, тем лучше”.
Например, для перехода к безразмерному показателю для натурального показателя “товарооборот” будет применяться формула (1.1), потому что по экономическому смыслу: “чем больше товарооборот, тем лучше”. В результате применения этой формулы тот объект, который имеет наибольшее значение показателя Xj (т.е., работает лучше всех), получает значение Yij=1. А тот объект, для которого Xj наименьшее (хуже всех работает), получает значение Yij=0. Остальные объекты получают значения безразмерного показателя от нуля до единицы соответственно уровню относительного успеха их работы.
Показатель “уровень издержек” по экономическому смыслу “чем меньше, тем лучше”, поэтому для него будет применяться формула (1.2). В результате применения этой формулы тот объект, который имеет наименьший уровень издержек (а, значит, работает лучше всех по этому показателю), получит значение Yij=1. Значение безразмерного показателя, равное 0, получит тот объект, у которого издержки были наибольшие.
Таким образом, безразмерный показатель не только позволяет обойти вопрос с единицами измерения, но и обеспечивает однозначное понимание того, какое значение является лучшим: для Yj лучше то значение, которое больше.
Далее находится суммарный комплексный показатель для каждого торгового объекта как сумма его безразмерных показателей:
 (1.3)
(1.3)
Иногда требуется проанализировать работу торговых объектов по нескольким натуральным показателям, причем важность каждого из них в анализе не одинакова. Для решения данной задачи каждому натуральному показателю назначается приоритет за счет введения весовых коэффициентов Pj (j=1,…,n) (ранги, баллы и т.п.), которые принимают значение от 0 до 1. Чем больше весовой коэффициент, тем важнее считается показатель.
Например, нужно проанализировать работу торговых объектов по трем показателям: товарооборот, рентабельность и фондоотдача; причем, наибольшее внимание обратить на товарооборот. В этом случае можно назначить весовые коэффициенты: P1=1 (для товарооборота), P2=0,9 (для рентабельности) и P3=0,9 (для фондоотдачи).
Суммарный комплексный показатель для каждого объекта в случае учета весовых коэффициентов находится по формуле:
 (1.4)
(1.4)
Чем больше значение Qi, тем лучше оценивается работа объекта.
Пример 1.1. Оценить торговую деятельность пяти РПС (m=5). Для оценки предлагается взять четыре показателя (n=4):
товарооборот в млн. руб.– X1,
охват доходов в % – X2,
уровень издержек в % – X3,
оборачиваемость в днях – X4.
Переоценить торговую деятельность РПС с учетом весовых коэффициентов Р1=1; Р2=0,7; Р3=0,9; Р4=0,7.
Исходные данные приведены в табл. 1.1.
Решение. Рассчитаем к безразмерные показатели. При переходе к безразмерным показателям для товарооборота X1 используем формулу (1.1), т.к. он по экономическому смыслу “чем больше, тем лучше”:
A1 = min (740,500,800,620,600)=500
В1 = max (740,500,800,620,600)=800
B1-A1=800-500=300
Y11=(740-500)/300=0,8
Y12=(500-500)/300=0
Y13=(800-500)/300=1
Y14=(620-500)/300=0,4
Y15=(600-500)/300=0,33
Для охвата доходов населения X2 также используем формулу (1.1), поскольку охват доходов чем больше, тем лучше:
A2 = min (60,75,75,90,70)=60
В2 = max (60,75,75,90,70)=90
B2-A2=90-60=30
Y21 =(60-60)/30=0
Y22 =(75-60)/30=0,5
Y23 =(75-60)/30=0,5
Y24 =(90-60)/30=1
Y25=(70-60)/30=0,33
Поскольку уровень издержек по экономическому смыслу “чем меньше, тем лучше”, используем для перехода к безразмерным показателям формулу (1.2):
A3 = min (5; 6,5; 6; 7; 4)=4
B3 = max (5; 6,5; 6; 7; 4)=7
B3-A3=7-4=3
Y31=(7-5)/3=0,67
Y32=(7-6,5)/3=0,17
Y33=(7-6)/3=0,33
Y34=(7-7)/3=0
Y34=(7-4)/3=1
Аналогично для оборачиваемости в днях также применяется формула (1.2):
A4 = min (70; 50; 90; 60; 75)=50
В4 = max (70; 50; 90; 60; 75)=90
B4-A4=90-50=40
Y41=(90-70)/40=0,5
Y42=(90-50)/40=1
Y43=(90-90)/40=0
Y44=(90-60)/40=0,75
Y45=(90-75)/40=0,38
Найдем суммарные комплексные показатели для каждого райпотребсоюза, используя формулу (1.3).
Q1=0,8+0+0,67+0,5=1,97
Q2=0+0,5+0,17+1=1,67
Q3=1+0,5+0,33+0=1,83
Q4=0,4+1+0+0,75=2,15
Q5=0,33+0,33+1+0,38=2,04
Результаты расчетов приведены в таблице 1.2.
Таблица 1.2. Комплексный анализ системы пяти РПС
| РПС, i | Показатели, j | ||||||||
| X1 | X2 | X3 | X4 | Y1 | Y2 | Y3 | Y4 | Q | |
| 1 2 3 4 5 | 740 500 800 620 600 | 60 75 70 90 80 | 5 6,5 6 7 4 | 70 50 90 60 75 | 0,8 0 1 0,4 0,33 | 0 0,5 0,5 1 0,33 | 0,67 0,17 0,33 0 1 | 0,5 1 0 0,75 0,38 | 1,97 1,67 1,83 2,15 2,04 |
| А=min | 500 | 60 | 4 | 50 |
|
|
|
|
|
| В=max | 800 | 90 | 7 | 90 |
|
|
|
|
|
| В-А | 300 | 30 | 3 | 40 |
|
|
|
|
|
Анализ найденных комплексных показателей Qi работы каждого РПС показывает, что наиболее эффективно работает четвертый РПС (Q4=2,15).
Переоценим торговую деятельность РПС с помощью весовых коэффициентов Р1=1; Р2=0,7; Р3=0,9; Р4=0,7 согласно формуле (1.4).
В лекции "О семиотике в психотерапии" также много полезной информации.
Q1* =0,8*1+0*0,7+0,67*0,9+0,5*0,7=1,75
Q2* =0*1+0,5*0,7+0,17*0,9+1*0,7=1,2
Q3* =1*1+0,5*0,7+0,33*0,9+0*0,7=1,65
Q4* =0,4*1+1*0,7+0*0,9+0,75*0,7=1,625
Q5* =0,33*1+0,33*0,7+1*0,9+0,38*0,7=1,73
С учетом весовых коэффициентов наиболее эффективно работает первый РПС (Q1*=1,75)























