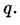Фракталы
ГЛАВА I. ФРАКТАЛЫ
Определение фрактала
Эти объекты вошли в научный обиход в 70-х годах прошлого века благодаря работам Бенуа Мандельброта. Фракталами называются геометричес- кие объекты – линии, поверхности, пространственные тела, – имеющие сильно изрезанную форму и обладающие свойством самоподобия. Слово фрактал произошло от латинского fractus и переводится как дробный, или ломаный. Самоподобие как основная характеристика фрактала означает, что он достаточно единообразно устроен в широком диапазоне масштабов. В идеальном случае самоподобие приводит к тому, что фрактальный объект оказывается инвариантным относительно растяжений, т. е., ему присуща дилатационная симметрия. Она предполагает неизменность основных геометрических особенностей фрактала при изменении масштаба.
Для реального природного фрактала существует некоторый минимальный масштаб длины lmin, такой, что на расстояниях l ≈ lmin, его основное свойство – самоподобие – пропадает. Кроме того, на достаточно больших масштабах длин l > lmах, где lmах – характерный геометрический размер объектов, свойство самоподобия также нарушается. Поэтому свойства природных фракталов рассматриваются лишь на масштабах l, удовлетворяющих соотношению lmin<< l << lmах , в так называемой, промежуточной асимптотике.
Как всякое фундаментальное понятие, фрактал не имеют определения и, следовательно, должен определятся списком свойств.
Тем не менее, существует как минимум три определения фракталов, безусловно, не являющихся полными, каждое из которых обращает внимание на некую существенную особенность этих объектов:
1. фрактал – это объект, в каком-то смысле подобный самому себе;
2. фрактал – это объект, размерность которого строго больше его топологической размерности;
3. фрактал – это объект, содержащий в себе "дыры" всех размеров, что фактически сводится к констатации его самоподобия на разных масштабах.
Рекомендуемые материалы
Классификация фракталов
Для того, чтобы представить все многообразие фракталов удобно прибегнуть к их общепринятой классификации
1. Регулярные (геометрические) фракталы
Свойства природных фрактальных объектов чрезвычайно разнообразны и сложны, поэтому для их исследования используются модельные фракталы, сгенерированные по специальным алгоритмам. Такие искусственные фрактальные объекты носят название регулярных фракталов. Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.
Триадная кривая Коха
Примером регулярных фракталов является триадная кривая Гельга фон Коха, т. н. «Снежинка Коха», процесс построения которой можно представить следующим образом (см. рисунок):
1. отрезок единичной длины l делится на 3 части, средняя часть отрезка отбрасывается и заменяется ломаной, состоящей из 2 отрезков длины 1/3;
2. каждый прямой отрезок полученной ломанной преобразуется согласно пункту 1, и мы получаем более изощренную ломаную линию;
3. пункты 1 и 2 повторяются до исчерпания технических возможностей чертежного приспособления.
На первом шаге алгоритма длина отрезка l составляет 1/3 от первоначальной. Тогда длина кривой Кох вычисляется просто
L = 4*1/3 = 4/3 = 1,33
На втором шаге алгоритма длина элементарного отрезка l = 1/9, длина кривой
L= 16*1/9 = 16/9 = 1,777
На третьем шаге алгоритма l = 1/27
L= 64*1/27 = 64/27 = 2,370370
и т.д. Можно заметить, что с увеличением количества стадий построения длина элементарного отрезка l ® 0, а длина кривой L стремится к бесконечности:
L= (4/3)n
l= (1/3)n ,
где n= 1,2,3.
|
|
Треугольник и квадрат Серпинского
Еще один пример регулярного фрактала – треугольник Вацлава Серпинского («Салфетка Серпинского»). Способ его построения ясен из рисунка: на нем представлен треугольник Серпинского на 3-й стадии построения, которая получена при соединении середин сторон соответствующих равносторонних треугольников.

На следующем рисунке – треугольник Серпинского, полученный при многократном соединении середин сторон соответствующих треугольников.

Аналогично можно построить ковер Серпинского, который является двумерным аналогом канторовского множества исключенных средних третей. Алгоритм его создания состоит в следующем. Каждая из сторон квадрата единичной площади делится на три равные части, а весь квадрат, соответственно, на девять одинаковых квадратиков со стороной, равной Из полученной фигуры вырезается центральный квадрат.
Из полученной фигуры вырезается центральный квадрат.

Затем такой же процедуре подвергается каждый из 8 оставшихся квадратиков и т. д.

В результате получается дырявый квадратный ковер Серпинского со значением фрактальной размерности
D = ln8 / ln3 = 1.8928 .
Он также представляет собой пример идеального самоподобного фрактала. Его фрактальная размерность, однако, больше, чем у салфетки Серпинского, т. е., он является в каком-то смысле «менее дырявым».
Губка Менгера
Алгоритм создания пространственного аналога квадратного ковра Серпинского, называемого губкой Менгера, состоит в следующем. Каждая грань куба, имеющая единичную длину, делится на 9 равных квадратиков так же, как и при построении квадратного ковра Серпинского. В результате исходный куб разбивается на 27 одинаковых кубиков с длиной ребра, равной Затем, удаляя 7 кубиков (один центральный и 6 из центра каждой из граней), противоположные грани исходного куба соединяются сквозным центральным отверстием квадратной формы. В результате из 27 остается 20 маленьких кубиков.
Затем, удаляя 7 кубиков (один центральный и 6 из центра каждой из граней), противоположные грани исходного куба соединяются сквозным центральным отверстием квадратной формы. В результате из 27 остается 20 маленьких кубиков.

Такая итерационная процедура с вырезанием сквозных отверстий и последующего превращения каждого оставшегося кубика в 20 еще более мелких кубиков с размером в три раза меныие исходного продолжается до бесконечности. В результате этих операций и образуется идеально самоподобный объект губка Менгера. Каждая грань исходного куба выглядит при этом так же, как ковер Серпинского.
Фрактальная размерность губки Менгера равна

Поскольку то губка имеет нулевой объем, но обладает бесконечной площадью поверхности своих пор.
то губка имеет нулевой объем, но обладает бесконечной площадью поверхности своих пор.
Легко заметить, что для фигур, обладающих свойством идеального самоподобия, правило позволяющее определить размерность  можно сформулировать следующим образом.
можно сформулировать следующим образом.
Если множество, состоящее из одинаковых элементов, строится с помощью самоподобного процесса, причем на любом шаге каждый из элементов с линейными размерами заменяется
заменяется  подобными элементами, размерами
подобными элементами, размерами каждый, то фрактальная размерность такого объекта очевидно равна
каждый, то фрактальная размерность такого объекта очевидно равна

Для всех рассмотренных выше регулярных фракталов фрактальная размерность оказалась меньше, чем размерность того пространства d в котором находится данный фрактальный объект. Неравенство
оказалась меньше, чем размерность того пространства d в котором находится данный фрактальный объект. Неравенство  отражает факт некомпактности фрактала, причем, чем больше различаются величины
отражает факт некомпактности фрактала, причем, чем больше различаются величины  и d , тем более рыхлым является фрактал.
и d , тем более рыхлым является фрактал.
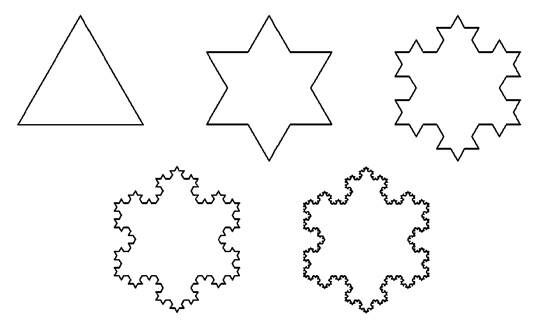
Кривая Госпера
Инициатором для кривой является отрезок единичной длины, а генератор показан на рисунке справа. Он состоит из 7 отрезков длиной каждый. Фрактальная размерность этой кривой равна 2.
каждый. Фрактальная размерность этой кривой равна 2.
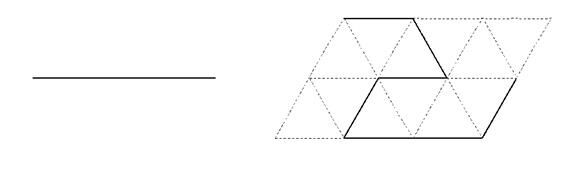
Пунктиром показана треугольная решетка, служащая своеобразной образующей для этого генератора. Следующие три шага процесса построения показаны на рисунке.
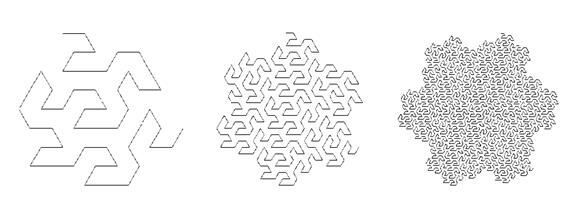
Интересной отличительной особенностью кривой Госпера является то, что граница области, называемой "островом Госпера", которую она заполняет в пределе бесконечного числа шагов, сама является фрактальной с нецелочисленной размерностью  1.1291. Такие острова можно использовать для непрерывного покрытия плоскости, так как можно показать, что они идеально стыкуются друг с другом. Более того, семь таких островов, состыкованных вместе (один в центре и шесть вокруг него), образуют снова остров Госпера в три раза большего размера. Заметим, что подобным свойством из правильных многоугольников обладает только квадрат.
1.1291. Такие острова можно использовать для непрерывного покрытия плоскости, так как можно показать, что они идеально стыкуются друг с другом. Более того, семь таких островов, состыкованных вместе (один в центре и шесть вокруг него), образуют снова остров Госпера в три раза большего размера. Заметим, что подобным свойством из правильных многоугольников обладает только квадрат.
Пример кривой Пеано – «дракон» Хартера-Хейтуэя
Рассмотрим кривую Пеано, для которой область, которую она заполняет на плоскости, имеет весьма причудливую форму. Это так называемый дракон Хартера-Хейтуэя. Первые 4 шага его построения изображены на рисунке. Как следует из рисунка, каждый из отрезков прямой
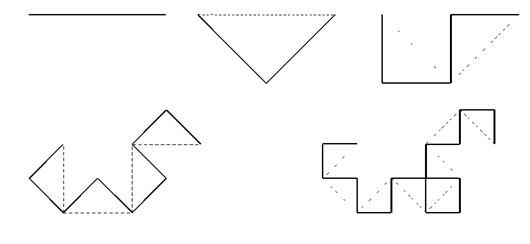
на следующем шаге заменяется на два отрезка, образующих боковые стороны равнобедренного прямоугольного треугольника, для которого исходный отрезок являлся бы гипотенузой. В результате отрезок как бы прогибается под прямым углом. Направление прогиба чередуется. Первый отрезок прогибается вправо (по ходу движения слева направо), второй – влево, третий – опять вправо и т. д. Для удобства восприятия на каждом рисунке пунктиром показана конфигурация предыдущего шага. Таким образом, после каждого шага число имеющихся отрезков удваивается, а длина каждого соответ-ственно уменьшается в раз. Поэтому фрактальная размерность образующейся в результате (после бесконечного числа шагов) кривой равна 2, т. е., кривая «заметает» собой конечную площадь. 0 форме образующейся необычной фигуры можно получить представление из рисунка, где изображены 12-е и 16-е "поколения" дракона. Дракон представляет собой своеобразную гирлянду в форме двухсторонней правой спирали, состоящую из подобных друг другу спиралевидных звеньев, непрерывно уменьшающихся в размерах от центра к периферии.
раз. Поэтому фрактальная размерность образующейся в результате (после бесконечного числа шагов) кривой равна 2, т. е., кривая «заметает» собой конечную площадь. 0 форме образующейся необычной фигуры можно получить представление из рисунка, где изображены 12-е и 16-е "поколения" дракона. Дракон представляет собой своеобразную гирлянду в форме двухсторонней правой спирали, состоящую из подобных друг другу спиралевидных звеньев, непрерывно уменьшающихся в размерах от центра к периферии.

Обратите внимание, что такой достаточно примитивный алгоритм приводит к столь необычной геометрической конструкции. Биологический подтекст, фигурирующий в названии кривой, заставляет задуматься, а не закодирована ли в генах каким-нибудь схожим простым образом информация о форме и размерах существующих в природе живых организмов? Рассмотренная выше кривая представляет собой лишь один из многих примеров так называемых Л-систем, изобретенных Аристидом Линденмаером в 1968 г. для моделирования биологического роста. Он показал, что предельная геометрия даже очень простых систем может быть фрактальной.
Вселенная Фурнье
В попытке понять устройство Вселенной учёные неизбежно сталкиваются с понятием фрактала.
Предположим, что нужно определить, с какой средней плотностью распределены звезды или галактики в видимой части Вселенной. Представим сферу достаточно большого радиуса  внутри которой находится очень много звезд. Тогда по определению средняя концентрация звезд
внутри которой находится очень много звезд. Тогда по определению средняя концентрация звезд  где
где — объем сферы. Можно предположить, что если радиус сферы достаточно велик, то концентрация звезд не будет зависеть от этого радиуса.
— объем сферы. Можно предположить, что если радиус сферы достаточно велик, то концентрация звезд не будет зависеть от этого радиуса.
Опытные данные, однако, говорят об обратном. С ростом величина п непрерывно уменьшается. И, что интересно, уменьшение происходит примерно по степенному закону
величина п непрерывно уменьшается. И, что интересно, уменьшение происходит примерно по степенному закону  , где
, где  т. е., намного меньше 3. Это соответствует тому, что число звезд в сфере радиуса
т. е., намного меньше 3. Это соответствует тому, что число звезд в сфере радиуса  растет как N = R1,23, т. е., гораздо медленнее, чем было бы в случае их однородного распределения в пространстве. Таким образом, распределение звезд и галактик во Вселенной сильно неоднородно. Количественной мерой этой неоднородности может служить отличие показателя степени
растет как N = R1,23, т. е., гораздо медленнее, чем было бы в случае их однородного распределения в пространстве. Таким образом, распределение звезд и галактик во Вселенной сильно неоднородно. Количественной мерой этой неоднородности может служить отличие показателя степени  от 3. Саму же величину
от 3. Саму же величину  можно отождествить с фрактальной размерностью распределения материи во Вселенной.
можно отождествить с фрактальной размерностью распределения материи во Вселенной.
Действительно, при определении, например, фрактальной размер-ности береговой линии, мы исходили из соотношения
береговой линии, мы исходили из соотношения  где величина
где величина была расстоянием между парой точек А и В на береговой линии по прямой, длина
была расстоянием между парой точек А и В на береговой линии по прямой, длина была нашим масштабом измерения, а число
была нашим масштабом измерения, а число показывало, сколько раз этот масштаб укладывался вдоль береговой линии между точками А и В. В соответствии с этой формулой фрактальную размерность
показывало, сколько раз этот масштаб укладывался вдоль береговой линии между точками А и В. В соответствии с этой формулой фрактальную размерность  можно трактовать двояко. С одной стороны, в полном согласии с определением она показывает, как с уменьшением масштаба
можно трактовать двояко. С одной стороны, в полном согласии с определением она показывает, как с уменьшением масштаба растет число элементов, с помощью которых можно покрыть некоторую выделенную область на данном фрактале. С другой стороны, она показывает, как то же число растет с увеличением
растет число элементов, с помощью которых можно покрыть некоторую выделенную область на данном фрактале. С другой стороны, она показывает, как то же число растет с увеличением  , размера этой области. Причина такой двойственности, очевидно, кроется в том, что у фрактала нет своего собственного масштаба длины, а поскольку число
, размера этой области. Причина такой двойственности, очевидно, кроется в том, что у фрактала нет своего собственного масштаба длины, а поскольку число должно быть безразмерным, то показатель степени
должно быть безразмерным, то показатель степени  оказывается одним и тем же как для зависимости
оказывается одним и тем же как для зависимости  так и для зависимости
так и для зависимости
Как можно себе наглядно представить распределение звезд в трехмерном пространстве, имеющее фрактальную размерность  близкую к единице? Разумеется, ответ на этот вопрос сильно неоднозначен. Существует бесконечное количество различных конструкций, имеющих одно и то же значение фрактальной размерности. Одним из классических примеров, который мы сейчас рассмотрим, является вселенная Фурнье, названная так по имени американского журналиста и изобретателя, который предложил ее в 1907 году. Она показана на рисунке.
близкую к единице? Разумеется, ответ на этот вопрос сильно неоднозначен. Существует бесконечное количество различных конструкций, имеющих одно и то же значение фрактальной размерности. Одним из классических примеров, который мы сейчас рассмотрим, является вселенная Фурнье, названная так по имени американского журналиста и изобретателя, который предложил ее в 1907 году. Она показана на рисунке.
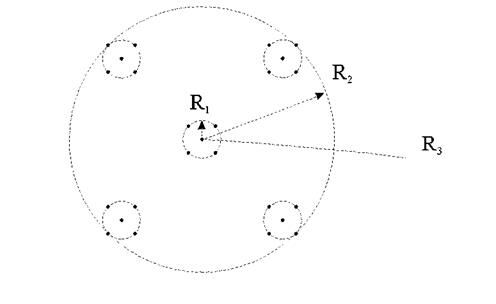
Каждая точка на этом рисунке представляет собой одну галактику. Они объединены в скопления радиуса  по 7 галактик в каждом скоплении. На рисунке видны только пять из них: недостающие две расположены симметрично над и под плоскостью рисунка, на прямой, проходящей через центр скопления. В свою очередь, семь таких скоплений аналогичным образом объединены в одно суперскопление радиуса
по 7 галактик в каждом скоплении. На рисунке видны только пять из них: недостающие две расположены симметрично над и под плоскостью рисунка, на прямой, проходящей через центр скопления. В свою очередь, семь таких скоплений аналогичным образом объединены в одно суперскопление радиуса Затем по такому же принципу из семи суперскоплений строится одно суперсуперскопление радиуса
Затем по такому же принципу из семи суперскоплений строится одно суперсуперскопление радиуса  , причем
, причем  и т. д. В результате многократного повторения такого процесса возникает самоподобная фрактальная структура.
и т. д. В результате многократного повторения такого процесса возникает самоподобная фрактальная структура.
Ее фрактальную размерность легко определить, заметив, что, как следует из рисунка, в сфере радиуса  содержится в семь раз больше галактик, чем в сфере радиуса
содержится в семь раз больше галактик, чем в сфере радиуса  , т. е.
, т. е.  Решением этого уравнения является степенная функция
Решением этого уравнения является степенная функция  где D=ln7/ln(R2/R1)
где D=ln7/ln(R2/R1)
У Фурнье  , поэтому размерность такой вселенной равняется 1. Как видно, она для этого вовсе не обязательно должна быть прямой или какой-нибудь другой плавной кривой. Более того, она даже не должна быть связной. Меняя отношение
, поэтому размерность такой вселенной равняется 1. Как видно, она для этого вовсе не обязательно должна быть прямой или какой-нибудь другой плавной кривой. Более того, она даже не должна быть связной. Меняя отношение легко построить фрактальные вселенные с другими размерностями
легко построить фрактальные вселенные с другими размерностями  близкими к единице.
близкими к единице.
2. Алгебраические фракталы
Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоваться терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д.
Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят – аттрактор (см. главу 4)) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом, фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то, окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры. Алгоритм его построения достаточно прост и основан на простом итеративном выражении:
Z[i+1] = Z[i] * Z[i] + C,
где Zi и C - комплексные переменные. Итерации выполняются для каждой стартовой точки C прямоугольной или квадратной области – подмножестве
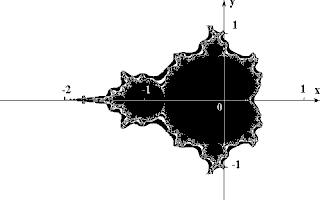
комплексной плоскости. Итерационный процесс продолжается до тех пор, пока Z[i] не выйдет за пределы окружности радиуса 2, центр которой лежит в точке (0,0), (это означает, что аттрактор динамической системы находится в бесконечности), или после достаточно большого числа итераций (например, 200-500) Z[i] сойдется к какой-нибудь точке окружности. В зависимости от количества итераций, в течении которых Z[i] оставалась внутри окружности, можно установить цвет точки C (если Z[i] остается внутри окружности в течение достаточно большого количества итераций, итерационный процесс прекращается и эта точка растра окрашивается в черный цвет).
Вышеописанный алгоритм дает приближение к так называемому множеству Мандельброта. Множеству Мандельброта принадлежат точки, которые в течение бесконечного числа итераций не уходят в бесконечность (точки имеющие черный цвет). Точки, принадлежащие границе множества (именно там возникает сложные структуры) уходят в бесконечность за конечное число итераций, а точки лежащие за пределами множества, уходят в бесконечность через несколько итераций (белый фон).
3. Стохастические фракталы
Известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные – несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.
Простейшим стохастическим фракталом является траектория частицы, совершающей брауновское движение.
Фрактальными свойствами обладают многие географические объекты –побережья, реки, горы, границы государств, если только они следуют естественным ориентирам, а не проведены линейкой по карте. Курьёзный факт: длина границы между Испанией и Португалией, приведенные в справочниках каждой из стран, отличаются на 20%, имеет несложное объяснение: при измерении использованы различные масштабы.
Для того, чтобы можно было говорить о фрактальных свойствах системы, необходимо, чтобы различие минимального и максимального масштабов было достаточно большим. Если речь идет о морском или океанском побережье, то максимальный масштаб будет порядка 1000 км, а минимальный, определяемый непостоянством границы из-за набегающих волн, приливов и отливов – порядка 1 – 10 м. Эти масштабы отличаются в миллион раз.
Существует множество физических процессов, приводящих к возникновению интересных и сложных фрактальных структур. Например, выращивание кристаллов из насыщенного раствора. Если раствор не слишком перенасыщен и достаточно хорошо перемешивается, то из подвешенной на нити затравки вырастает красивый кристалл правильной формы. Кристалл растет из-за того, что в своем тепловом движении какие - то молекулы подходят к тем местам на его поверхности, где они могут "прилипнуть", заняв наиболее выгодное с энергетической точки зрения положение. Конечно, большинство молекул попадает в не совсем подходящие места, однако рано или поздно они снова переходят в раствор или расплав из-за недостаточной связи с остальным кристаллом. В результате такого равновесного роста получается кристалл без внутренних пустот, с идеально гладкими плоскими гранями.
При отсутствии равновесия между кристаллизацией и растворением (т.е., при быстрой кристаллизации из сильно пересыщенного раствора или при кристаллизации из газовой фазы) появляются кристаллы совсем другого вида. Как, например, морозные узоры на окнах. Эти довольно рыхлые образования возникают из-за осаждения содержащейся в воздухе воды. Сначала образуются отдельные скопления молекул – так называемые кластеры; постепенно разрастаясь и соединяясь, кластеры и образуют узоры. Условия, сходные с теми, что имеют место при росте кластеров, существуют и при росте снежинок в облаке.
Такой процесс роста, называемый диффузионно-контролируемой агрегацией, приводит к возникновению кристалликов фрактальной формы – дендритов. В зависимости от взаимодействия образующих кристалл молекул и от размера самого кристалла дендрит может быть случайной, неправильной формы или, напротив, казаться идеально правильной фигурой, как хорошо знакомые всем снежинки. В действительности о правильной форме снежинок можно говорить лишь на достаточно больших масштабах (на размерах самой снежинки), а на малых масштабах никакой регулярности нет – это отражает те случайные процессы, которые привели к их образованию.
Очень похожие на дендритные кристаллы фигуры возникают при электрическом пробое диэлектриков. Если сильная электрическая искра ударяет в диэлектрическую пластинку, на ее поверхности остается отчетливо видимый узор – так называемые фигуры Г. Лихтенберга.
Фрактальными свойствами обладают многие системы, давно используемые для вполне практических целей. Например, поверхность активированного угля, используемого в качестве сорбента в противогазах, является фрактальной. Размерность этой поверхности больше 2: она имеет чрезвычайно большую (формально – бесконечную, в том же смысле, в каком бесконечна длина кривой Коха) площадь и выемки всех масштабов, способные поймать и надежно удержать частицу любого размера – от пылинки до большой молекулы. Фрактальной является также поверхность многих используемых в химии твердых кристаллизаторов.
Идея размерности
В евклидовом пространстве RE величины топологической размерности DT и фрактальной размерности D заключены в промежутке от 0 до E. При этом размерность DT всегда является целым числом, в то время как для размерности D это не обязательно. Эти две размерности могут не совпадать, они должны лишь удовлетворять неравенству Спилрайна D > DT . В случае же евклидовых множеств D = DT .
Таким образом, фракталом будем называть такое множество, для которого фрактальная размерность строго больше его топологической размерности.
Эффективная размерность
Помимо математических идей, лежащих в основе размерностей D и DT, воспользуемся понятием эффективной размерности, которая выражает соотношение между математическими множествами и естественными объектами, обусловлена приближением и, как следствие, степенью разрешения и неизбежно опирается на субъективный фундамент. Для примера возьмем шар диаметром 10 см, скрученный из толстой нити диаметром 1 мм.
Удаленному наблюдателю клубок покажется фигурой с нулевой размерностью, т.е., точкой. С расстояния в 10 см шар из нитей выглядит как трехмерное тело, а с расстояния в 10 мм – как беспорядочное переплетение одномерных нитей. На расстоянии в 0,1 мм каждая нить превратится в толстую колонну, а вся структура целиком опять станет трехмерным телом. На расстоянии 0,01 мм колонны превратятся в переплетение волокон, и шар снова станет одномерным. При дальнейшем приближении процесс становится периодическим – размерность наблюдаемой фигуры переключается с одного значения на другое и наоборот. Наконец, когда клубок превратится в скопление, состоящее из какого-то конечного числа точек, имеющих размеры порядка атомных, его размерность станет снова равной нулю. Похожую последовательность смены размерностей можно наблюдать при разглядывании листа бумаги.
Как измерить размерность
Воспользуемся еще одним определением размерности, которым часто пользуются при экспериментальном измерении размерности различных физических систем.
Пространство, в котором расположен интересующий нас объект, разбивают на клетки размером l (например, наносят на плоскость фотографии объекта квадратную сетку со стороной l). Подсчитывают число клеток, в которые попали точки объекта. Разбиение повторяют, используя меньший масштаб l¢ < l и т.д. Зависимость числа клеток, в которые попали точки объекта, от размера клетки при этом дается законом N = Аl-D , где D и есть искомая размерность. Для определения размерности реальных объектов рисуют график зависимости lnN от lnl. Этот график изображается прямой линией, тангенс угла наклона которой дает нам значение D.
Самоподобие фракталов
Однородное распределение вдоль линии, на плоскости или в пространстве обладает двумя свойствами: оно инвариантно при смещении и при изменении масштаба. При переходе к фракталам обе инвариантности неизбежно подвергаются модификации или ограничению области их действия. Следовательно, "наилучшими" можно считать фракталы, которые демонстрируют максимальную инвариантность.
В случае смещения различные участки траектории брауновского движения частицы не могут быть точно совмещены друг с другом, как, например, могут быть совмещены различные участки прямой линии. Тем не менее, можно считать, что эти участки совместимы в статистическом смысле. Почти все фракталы в той или иной степени инвариантны при смещении.
Более того, большинство фракталов инвариантны при некоторых преобразованиях масштаба. Будем называть их масштабно-инвариантными фракталами. Фрактал, инвариантный при обычном геометрическом преобразовании подобия, называется самоподобным.
МУЛЬТИФРАКТАЛЫ
Геометрическое описание мультифракталов
Мультифракталы – неоднородные фрактальные объекты, для описания которых недостаточно, в отличие от регулярных фракталов, введения одной величины – его фрактальной размерности D, а необходим целый спектр таких размерностей, число которых бесконечно. Проще всего пояснить, что понимается под "неоднородным фракталом" на примере треугольника Серпинского.
Допустим, что в методе случайных итераций по какой-то причине отдали предпочтение одной из вершин треугольника, например, некой вершине А, и стали выбирать ее с вероятностью 90%. Две же остальные вершины Β и С по-прежнему равноценны, но на их долю теперь приходится всего лишь по 5%. Ясно, что точки внутри треугольника распределены теперь крайне неравномерно. Большая их часть находится у вершины Α и ее прообразов. Β тο же время у вершин Β и С (и их прообразов) их имеется крайне мало. По обычной терминологии данное множество точек (при стремлении числа итераций κ бесконечности) является фракталом, так как сохранилось основное свойство фрактала – самоподобие.
На рисунке детально показано результирующее распределение точек по треугольнику Серпинского. Цифры в каждом из маленьких треугольников показывают его относительную заселенность точками множества.

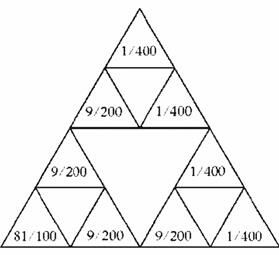
Однако несмотря на неравномерность распределения точек по фракталу, его фрактальная размерность осталась при этом прежней,  Покрытие этого множества все более и более мелкими треугольниками можно осуществить по тому же алгоритму, что и ранее. Такое совпадение заставляет заняться поиском иных количественных характеристик, которые могли бы отличить неравномерное распределение точек от равномерного.
Покрытие этого множества все более и более мелкими треугольниками можно осуществить по тому же алгоритму, что и ранее. Такое совпадение заставляет заняться поиском иных количественных характеристик, которые могли бы отличить неравномерное распределение точек от равномерного.
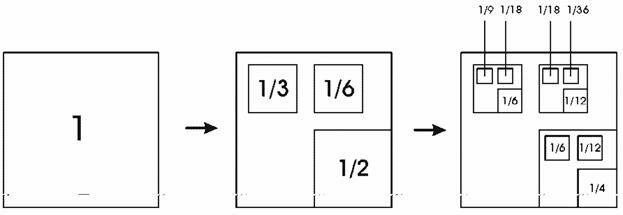
Другой, более сложный пример неоднородного фрактала показан на следующем рисунке. Здесь слева показан большой квадрат со стороной, равной единице, который на этом (нулевом) этапе полностью покрывает собой некоторое фрактальное множество точек На следующем (первом) этапе, в центре рисунка, показано, как то же самое множество можно покрыть тремя меньшими квадратами со сторонами
На следующем (первом) этапе, в центре рисунка, показано, как то же самое множество можно покрыть тремя меньшими квадратами со сторонами в которых, содержится доля
в которых, содержится доля  всех точек, соответственно.
всех точек, соответственно.
Следующий этап покрытия (изображенный на рисунке справа) со-держит уже 9 квадратиков со сторонами (в нижнем правом углу) и
(в нижнем правом углу) и  (вверху справа и слева). Относительная заселенность этих квадратиков точками множества показана на рисунке. Она соответствует произведению факторов заселенностей (вероятностей):
(вверху справа и слева). Относительная заселенность этих квадратиков точками множества показана на рисунке. Она соответствует произведению факторов заселенностей (вероятностей):

 – для нижней правой группы,
– для нижней правой группы,
 – для верхней левой и
– для верхней левой и  – для верхней правой группы. Отметим, что имеется строгое соответствие между заселенностью квадратика
– для верхней правой группы. Отметим, что имеется строгое соответствие между заселенностью квадратика  и его размерами
и его размерами 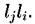
Дальнейший процесс разбиения и покрытия множества М. осу-ществляется в соответствии с этой ренормализационной схемой. Каждый квадратик, имеющий на n-м шаге размер l и заселенность р, заменяется на п+1 шаге на три квадратика с размерами  и заселенностями
и заселенностями  соответственно, расположенными таким же образом относи тельно друг друга, как показано на рисунке в центре .
соответственно, расположенными таким же образом относи тельно друг друга, как показано на рисунке в центре .
Два рассмотренных выше случая представляют собой примеры не-однородных фракталов. Под словом "неоднородный" понимается неравномерное распределение точек множества по фракталу. Причина неоднородности в обоих случаях – разные вероятности заполнения геометрически одинаковых элементов фрактала, или в общем случае несоответствие вероятностей заполнения геометрическим размерам соответствующих областей. Такие неоднородные фрактальные объекты в литературе называются мультифракталами.
Обобщенные размерности А. Реньи. Определение мультифрактала
Рассмотрим фрактальный объект, занимающий некую ограниченную область размера L в эвклидовом пространстве с размерностью d. Пусть на каком-то этапе его построения он представляет собой множество из
размера L в эвклидовом пространстве с размерностью d. Пусть на каком-то этапе его построения он представляет собой множество из точек, как-то распределенных в этой области. Предположим, что
точек, как-то распределенных в этой области. Предположим, что  Примером такого множества может служить треугольник Серпинского, построенный методом случайных итераций. Каждый шаг итерационной процедуры добавляет к этому множеству одну новую точку.
Примером такого множества может служить треугольник Серпинского, построенный методом случайных итераций. Каждый шаг итерационной процедуры добавляет к этому множеству одну новую точку.
Разобьем всю область на кубические ячейки со стороной
на кубические ячейки со стороной и объемом
и объемом Далее нас будут интересовать только занятые ячейки, в которых содержится хотя бы одна точка. Пусть номер занятых ячеек і изменяется в пределах
Далее нас будут интересовать только занятые ячейки, в которых содержится хотя бы одна точка. Пусть номер занятых ячеек і изменяется в пределах – суммарное количество занятых ячеек, которое, конечно, зависит от размера ячейки
– суммарное количество занятых ячеек, которое, конечно, зависит от размера ячейки
Пусть представляет собой количество точек в ячейке с номером і, тогда величина
представляет собой количество точек в ячейке с номером і, тогда величина

представляет собой вероятность того, что наугад взятая точка из нашего множества находится в ячейке і. Другими словами, вероятнос-ти характеризуют относительную заселенность ячеек. Из условия нормировки вероятности следует, что
характеризуют относительную заселенность ячеек. Из условия нормировки вероятности следует, что

Введем в рассмотрение обобщенную статистическую сумму характеризуемую показателем степени q, который может принимать любые значения в интервале
характеризуемую показателем степени q, который может принимать любые значения в интервале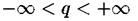
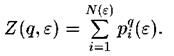
Венгерский математик Альфред Реньи предложил понятие спектра обобщенных фрактальных размерностей  характеризующих данное распределение точек в области
характеризующих данное распределение точек в области  которое определяется с помощью соотношения
которое определяется с помощью соотношения

где функция  имеет вид
имеет вид

Известно, если  т. е., не зависит от q, то данное множество точек представляет собой обычный, регулярный фрактал, который характеризуется всего лишь одной величиной – фрактальной размерностью D. Напротив, если функция
т. е., не зависит от q, то данное множество точек представляет собой обычный, регулярный фрактал, который характеризуется всего лишь одной величиной – фрактальной размерностью D. Напротив, если функция как-то меняется с q, то рассматриваемое множество точек является мультифракталом.
как-то меняется с q, то рассматриваемое множество точек является мультифракталом.
Таким образом, мультифрактал в общем случае характеризуется некоторой нелинейной функцией  определяющей поведение статистической суммы
определяющей поведение статистической суммы при
при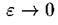
 (*)
(*)
Следует иметь в виду, что в реальной ситуации всегда имеем конечное, хотя и очень большое число дискретных точек N, поэтому при компьютерном анализе конкретного множества предельный пере-ход надо выполнять с осторожностью, помня, что ему всегда предшествует предел
надо выполнять с осторожностью, помня, что ему всегда предшествует предел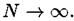
Покажем, как ведет себя обобщенная статистическая сумма в случае обычного регулярного фрактала с фрактальной размерностью D. В этом случае во всех занятых ячейках содержится одинаковое количество точек
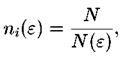
то есть, фрактал является однородным. Тогда очевидно, что относительные населенности всех ячеек, тоже одинаковы, и обобщенная статистическая сумма принимает вид
тоже одинаковы, и обобщенная статистическая сумма принимает вид
 (**)
(**)
Учтем, что согласно определению фрактальной размерности D, число занятых ячеек при достаточно малом ведет себя следующим образом
ведет себя следующим образом
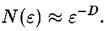
Подставляя это выражение в формулу (**) и сравнивая с (*), приходим к выводу, что в случае обычного фрактала функция

т. е., является линейной. Тогда все  и действительно не зависят от q. Для фрактала, все обобщенные фрактальные размерности
и действительно не зависят от q. Для фрактала, все обобщенные фрактальные размерности  которого совпадают, часто используется термин монофрактал.
которого совпадают, часто используется термин монофрактал.
Если распределение точек по ячейкам неодинаково, то фрактал является неоднородным, т. е., представляет из себя мультифрактал, и для его характеристики, как отмечалось, необходим целый спектр обобщенных фрактальных размерностей число которых, в общем случае, бесконечно.
число которых, в общем случае, бесконечно.
Так, например, при основной вклад в обобщенную статистическую сумму вносят ячейки, содержащие наибольшее число частиц
основной вклад в обобщенную статистическую сумму вносят ячейки, содержащие наибольшее число частиц  в них и, следовательно, характеризующиеся наибольшей вероятностью их заполнения
в них и, следовательно, характеризующиеся наибольшей вероятностью их заполнения Наоборот, при
Наоборот, при основной вклад в сумму дают самые разреженные ячейки с малыми значениями чисел заполнения
основной вклад в сумму дают самые разреженные ячейки с малыми значениями чисел заполнения  Таким образом, функция
Таким образом, функция показывает, насколько неоднородным является исследуемое множество точек
показывает, насколько неоднородным является исследуемое множество точек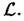
В дальнейшем для характеристики распределения точек необходимо знать не только функцию но и ее производную
но и ее производную
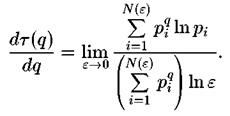
Эта призводная имеет важный физический смысл. Если она не остается постоянной и меняется с q, то это означает, что исследуемый объект мультифрактал.
Фрактальная и информационная размерность
Выясним физический смысл обобщенных фрактальных размерностей  для некоторых конкретных значений q.
для некоторых конкретных значений q.
Если , то
, то  и
и 
Сопоставляя эти два равенства, получим Это означает, что величина
Это означает, что величина , называемая фрактальной размерностью, представляет собой обычную хаусдорфову размерность множества
, называемая фрактальной размерностью, представляет собой обычную хаусдорфову размерность множества Она является наиболее грубой характеристикой мультифрактала и не несет информации о его статистических свойствах.
Она является наиболее грубой характеристикой мультифрактала и не несет информации о его статистических свойствах.
Определим смысл величины Поскольку при
Поскольку при в силу условия нормировки вероятности статистическая сумма равна
в силу условия нормировки вероятности статистическая сумма равна 
то Таким образом, имеем неопределенность в выражении для
Таким образом, имеем неопределенность в выражении для . Раскроем эту неопределенность с помощью равенства
. Раскроем эту неопределенность с помощью равенства
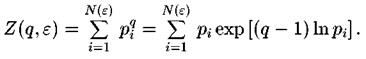
Устремляя раскладывая экспоненту и учитывая условие нормировки, получим
раскладывая экспоненту и учитывая условие нормировки, получим

В результате получим

С точностью до знака числитель в этой формуле представляет собой энтропию фрактального множества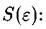
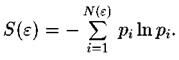
Такое определение энтропии множества полностью идентично используемому в термодинамике, где под понимается вероятность об-наружить систему в квантовом состоянии і. В результате величина обобщенной фрактальной размерности
понимается вероятность об-наружить систему в квантовом состоянии і. В результате величина обобщенной фрактальной размерности связана с энтропией
связана с энтропией соотношением
соотношением
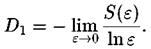
Прежде чем далее характеризовать эту величину, напомним, что в термодинамике энтропия есть мера беспорядка в системе. Простой пример, где молекулы газа, помещенные вначале в одну половину сосуда, заполняют весь сосуд, когда убирается перегородка, показывает, что в этом процессе беспорядок, а следовательно, энтропия возрастает. Этот рост беспорядка связан с ростом нашего незнания о состоянии системы, поскольку до удаления перегородки мы знали больше о расположении молекул.
Основываясь на подобных соображениях, Клод Шенон обобщил понятие энтропии известное в термодинамике, на абстрактные задачи теории передачи и обработки информации. Для этих задач энтропия стала мерой количества информации, необходимой для определения системы в некотором положении і. Другими словами, она является мерой нашего незнания о системе.
известное в термодинамике, на абстрактные задачи теории передачи и обработки информации. Для этих задач энтропия стала мерой количества информации, необходимой для определения системы в некотором положении і. Другими словами, она является мерой нашего незнания о системе.
Поясним эти соображения на простом примере. Допустим, имеется ящик с двумя отделениями, в одном из которых находится точка. Однако мы не знаем, в каком. Спрашивается, сколько вопросов с ответом «да» или «нет » нужно задать, чтобы определить местоположение точки? Ответ очевиден – один вопрос. Эту информацию принимают за единицу и называют ее бит.
Для обнаружения точки в ящике с четырьмя возможными состояниями требуется уже два вопроса, и, соответственно, мера нашего незнания о системе равна двум битам. Эту информацию можно записать как логарифм по основанию два от числа возможных состояний системы 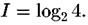
Теперь становится понятно, что справедливо логарифмическое соот-ношение между максимальным количеством информации I и числом состояний М  Так, например, чтобы определить положение точки на шахматной доске с
Так, например, чтобы определить положение точки на шахматной доске с клетками, требуется 6 вопросов.
клетками, требуется 6 вопросов.
В предыдущем случае ящика с двумя состояниями количество ин-формации в один бит можно выразить также следующим образом
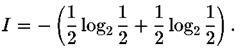
Учитывая, что – есть вероятность обнаружить систему в одном из ящиков, эту формулу можно переписать так
– есть вероятность обнаружить систему в одном из ящиков, эту формулу можно переписать так 
В таком виде она справедлива и в случае ящика с состояниями, где все вероятности
состояниями, где все вероятности одинаковы. Более того (и это как раз и составляет результат, полученный К. Шеноном), эта формула остается справедливой и в случае неравных вероятностей
одинаковы. Более того (и это как раз и составляет результат, полученный К. Шеноном), эта формула остается справедливой и в случае неравных вероятностей однако ее нужно тогда понимать в смысле среднего значения по большому числу испытаний. Отсюда уже остается всего один шаг до соотношения между энтропией
однако ее нужно тогда понимать в смысле среднего значения по большому числу испытаний. Отсюда уже остается всего один шаг до соотношения между энтропией и количеством информации
и количеством информации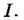
Возвращаясь к исходной задаче о распределении точек на фрактальном множестве можно сказать, что поскольку
можно сказать, что поскольку  то величина
то величина  характеризует информацию, необходимую для определения местоположения точки в некоторой ячейке. В связи с этим обобщенную фрактальную размерность
характеризует информацию, необходимую для определения местоположения точки в некоторой ячейке. В связи с этим обобщенную фрактальную размерность часто называют информационной размерностью. Она показывает, как информация, необходимая для определения местоположения точки, возрастает при стремлении размера ячейки
часто называют информационной размерностью. Она показывает, как информация, необходимая для определения местоположения точки, возрастает при стремлении размера ячейки к нулю.
к нулю.
Корреляционная размерность
Определим физический смысл обобщенной фрактальной размерности Для нее справедливо следующее выражение
Для нее справедливо следующее выражение

Определим парный корреляционный интеграл
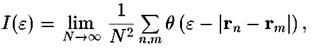
где суммирование проводится по всем парам точек нашего фрактального множества с радиус-векторами и
и  ;
; – ступенчатая функция Хевисайда,
– ступенчатая функция Хевисайда,  если
если и
и , если
, если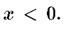
Сумма в выражении для D2 определяет число пар точек (n, m), для которых расстояние между ними меньше, чем Поэтому, поделенная на
Поэтому, поделенная на она определяет вероятность того, что две наугад взятые точки разделены расстоянием меныиим, чем
она определяет вероятность того, что две наугад взятые точки разделены расстоянием меныиим, чем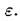
Эту же вероятность можно определить и по-другому. Величина согласно своему определению, представляет собой вероятность попадания точки в і-ю ячейку с размером
согласно своему определению, представляет собой вероятность попадания точки в і-ю ячейку с размером  Следовательно, величи-на
Следовательно, величи-на представляет собой вероятность попадания в эту ячейку двух точек. Суммируя
представляет собой вероятность попадания в эту ячейку двух точек. Суммируя по всем занятым ячейкам, мы получаем вероятность того, что две произвольно выбранные точки из множества
по всем занятым ячейкам, мы получаем вероятность того, что две произвольно выбранные точки из множества лежат внутри одной ячейки с размером
лежат внутри одной ячейки с размером Следовательно, расстояние между этими точками будет меныие или порядка
Следовательно, расстояние между этими точками будет меныие или порядка Таким образом, с точностью до численных коэффициентов
Таким образом, с точностью до численных коэффициентов
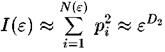
Таким обазом, обобщенная размерность определяет зависимость корреляционного интеграла
определяет зависимость корреляционного интеграла от
от в пределе
в пределе По этой причине величину
По этой причине величину в литературе называют корреляционной размерностью.
в литературе называют корреляционной размерностью.
Свойства функции Dq
Мультифрактал характеризуется неоднородным распределением точек по ячейкам. Как известно из термодинамики, энтропия неоднородного распределения молекул газа в сосуде всегда меньше энтропии их однородного распределения (в том же сосуде), когда газ везде обладает одной и той же плотностью. Соответственно, если бы точки, составляющие мультифрактал, были бы распределены по нему равномерно по всем  ячейкам с вероятностью
ячейкам с вероятностью  энтропия такого распределения была бы максимальна и равна
энтропия такого распределения была бы максимальна и равна
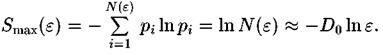
Другими словами, она была бы больше фактической величины энтропии мультифрактала, рассчитанной для реального неоднородного распределения точек, Отсюда следует важный вывод, что информационная размерность мультифрактала
Отсюда следует важный вывод, что информационная размерность мультифрактала всегда меньше или равна его хаусдорфовой размерности
всегда меньше или равна его хаусдорфовой размерности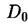
Это неравенство можно обобщить для произвольного показателя степени и доказать, что обобщенная фрактальная размерность
и доказать, что обобщенная фрактальная размерность всегда монотонно убывает или остается постоянной с ростом q
всегда монотонно убывает или остается постоянной с ростом q 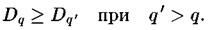
Знак равенства имеет место, например, для однородного фрактала. Максимального значения  величина
величина достигает при
достигает при  , а минимального
, а минимального при
при
Неоднородное канторово множество
Рассмотрим простой пример, который позволит вычислить спектр обобщенных фрактальных размерностей  аналитически и продемонстри ровать основные свойства функции
аналитически и продемонстри ровать основные свойства функции Рассмотрим канторово множество исключенных средних третей. Пусть в начале процедуры (нулевой шаг) у нас имеется единичный отрезок, по которому как-то распределены N точек нашего фрактального множества. На первом шаге имеем 2 отрезка по краям первоначального единичного интервала, каждый из них длиной 1/3. Пусть наши исходные N точек распределены по ним теперь следующим образом. Левый отрезок заселен с вероятностью
Рассмотрим канторово множество исключенных средних третей. Пусть в начале процедуры (нулевой шаг) у нас имеется единичный отрезок, по которому как-то распределены N точек нашего фрактального множества. На первом шаге имеем 2 отрезка по краям первоначального единичного интервала, каждый из них длиной 1/3. Пусть наши исходные N точек распределены по ним теперь следующим образом. Левый отрезок заселен с вероятностью и имеет
и имеет точек, а правый с вероятностью
точек, а правый с вероятностью  и на нем, соответственно, находится
и на нем, соответственно, находится точек. Затем с каждым из этих отрезков поступаем аналогичным образом. В результате на втором шаге имеется 4 отрезка длиной 1/9, заселенных с вероятностью (слева направо)
точек. Затем с каждым из этих отрезков поступаем аналогичным образом. В результате на втором шаге имеется 4 отрезка длиной 1/9, заселенных с вероятностью (слева направо) и т. д.(см. рисунок).
и т. д.(см. рисунок).
Повторяя эту процедуру некоторое число раз, приходим к следующей картине распределения точек. На шаге n множество состоит из  отрезков
отрезков
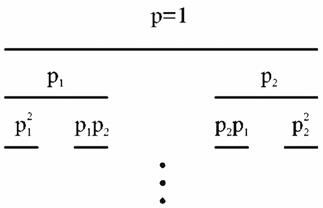
длиной , заселенных с вероятностями
, заселенных с вероятностями

 .
.
Видно, что число отрезков, характеризуемых вероятностью  равно
равно , т. е., числу сочетаний из
, т. е., числу сочетаний из элементов по
элементов по В результате при
В результате при  и
и  приходим к неоднородному фрактальному множеству.
приходим к неоднородному фрактальному множеству.
На  шаге процедуры обобщенная статистическая сумма мультифрактала имеет вид обычного бинома Ньютона
шаге процедуры обобщенная статистическая сумма мультифрактала имеет вид обычного бинома Ньютона
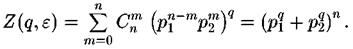
Поскольку на этом шаге размер ячейки то получим уравнение для спектра обобщенных фрактальных размерностей
то получим уравнение для спектра обобщенных фрактальных размерностей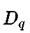

Устремляя с учетом определения
с учетом определения находим
находим
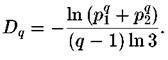
Если то имеем однородный фрактал, все обобщенные фрактальные размерности
то имеем однородный фрактал, все обобщенные фрактальные размерности которого одинаковы и равны хаусдорфовой размерности исходного канторова множества исключенных средних третей
которого одинаковы и равны хаусдорфовой размерности исходного канторова множества исключенных средних третей

Если же  то канторово множество является неоднородным. На следующем рисунке изображена зависимость
то канторово множество является неоднородным. На следующем рисунке изображена зависимость для значения вероятности
для значения вероятности 
Значение хаусдорфовой размерности  совпадает в этом случае с размерностью однородного канторовского множества.
совпадает в этом случае с размерностью однородного канторовского множества.
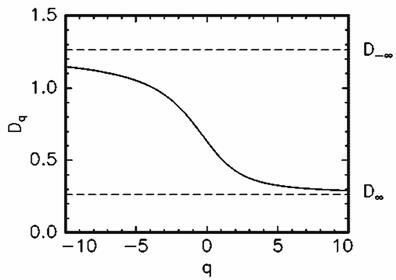
Это естественно, так как множество расположено на фрактале с этим значением размерности. Этот фрактал в литературе имеет специальное название – носитель исходного мультифрактального множества. По этой причине величину  часто называют размерностью носителя мультифрактала.
часто называют размерностью носителя мультифрактала.
Раскроем неопределенность в формуле  Получим информационную размерность
Получим информационную размерность
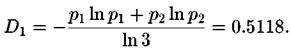
Она, как и следовало ожидать, меньше размерности  а корреляционная размерность
а корреляционная размерность в свою очередь, меньше, чем
в свою очередь, меньше, чем . Таким образом, в этом случае
. Таким образом, в этом случае является монотонно убывающей функцией
является монотонно убывающей функцией .
.
Предельных значений эта функция достигает, как мы говорили, при . Эти значения
. Эти значения и
и равны
равны
 и
и 
Носитель мультифрактального множества может сам по себе и не являться фракталом. Например, если исходный единичный отрезок в предыдущем примере разделим на первом шаге на 2 равные части с длиной 1/2. Первой части припишем вероятность (меру) а второй
а второй Далее с каждым из двух образовавшихся отрезков поступим аналогичным образом и т. д. Нетрудно понять, что спектр обобщенных фрактальных размерностей будет определятся из выражения
Далее с каждым из двух образовавшихся отрезков поступим аналогичным образом и т. д. Нетрудно понять, что спектр обобщенных фрактальных размерностей будет определятся из выражения

Рекомендация для Вас - 5 Развитие патологических реакций на вакцинацию у детей.
В этом случае размерность так как теперь носителем нашего мультифрактала является весь единичный отрезок целиком, т. е., объект с пространственной размерностью
так как теперь носителем нашего мультифрактала является весь единичный отрезок целиком, т. е., объект с пространственной размерностью равной единице. Все остальные обобщенные фрактальные размерности заключены в интервале между
равной единице. Все остальные обобщенные фрактальные размерности заключены в интервале между
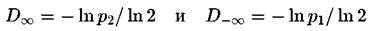
 . График функции
. График функции в этом случае выглядит качественно так же, как показано на предыдущем рисунке.
в этом случае выглядит качественно так же, как показано на предыдущем рисунке.
В результате приходим к выводу, что набор различных значений функции представляют собой спектр фрактальных размерностей однородных подмножеств
представляют собой спектр фрактальных размерностей однородных подмножеств на которые можно разбить исходное множество
на которые можно разбить исходное множество Отсюда становится понятным термин мультифрактал. Его можно понимать как некое объедине-ние различных однородных фрактальных подмножеств
Отсюда становится понятным термин мультифрактал. Его можно понимать как некое объедине-ние различных однородных фрактальных подмножеств , исходного множества
, исходного множества каждое из которых имеет свое собственное значение фрактальной размерности
каждое из которых имеет свое собственное значение фрактальной размерности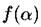
Поскольку любому подмножеству принадлежит лишь часть от общего числа ячеек на которые разбито исходное множество
на которые разбито исходное множество условие нормировки вероятностей, очевидно, не выполняется при суммировании только по этому подмножеству. Сумма этих вероятностей оказывается меньше единицы. Поэтому и сами вероятности
условие нормировки вероятностей, очевидно, не выполняется при суммировании только по этому подмножеству. Сумма этих вероятностей оказывается меньше единицы. Поэтому и сами вероятности с одним и тем же значением
с одним и тем же значением очевидно меньше (или в крайнем случае одного порядка), чем величина
очевидно меньше (или в крайнем случае одного порядка), чем величина , которая обратно пропорциональна числу имеющихся ячеек, покрывающих данное подмножество (напомним, что в случае монофрактала
, которая обратно пропорциональна числу имеющихся ячеек, покрывающих данное подмножество (напомним, что в случае монофрактала ).
).
Таким образом, при всех значениях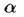
 Знак равенства имеет место, например, для полностью однородного фрактала, где
Знак равенства имеет место, например, для полностью однородного фрактала, где Это свойство тесно связано со свойством функции
Это свойство тесно связано со свойством функции которая либо монотонно убывает, либо остается постоянной при увеличении
которая либо монотонно убывает, либо остается постоянной при увеличении