Быстрые схемы дискретного преобразования Фурье

Лекция 14. Быстрые схемы дискретного преобразования Фурье.

Обычные формулы для вычисления ДПФ требуют большого количества умножений: , где  - число точек в ДПФ. Существуют приемы, позволяющие уменьшить это количество. Они называются быстрыми схемами (БПФ). Простейшая относится к случаю .

Случай

 Любое число в интервале  однозначно представляется двоичным вектором длины . Если последовательность  задана, то положим

. В дальнейшем, что упростить изложение, введем обозначение , откуда . Имеем

. Основное замечание заключается в следующем: суммирование по индексу  равносильно суммированию по всем двоичным индексам .

, каждый из которых принимает два значения.

Для числа  существует аналогичное двоичное представление:. Рассмотрим самую внутреннюю сумму. . Нетрудно видеть, что это некоторая функция . Следующая сумма принимает вид . Этот процесс продолжается. Окончательно имеем . Количество сумм равняется , в каждой из которых лишь одно умножение. Для вычисления всех коэффициентов нужно  умножений. Другое преимущество этой схемы - экономный расход оперативной памяти.

Случай   с взаимно простыми сомножителями

Рассмотрим другой крайний случай, когда  и . В этом случае существуют целые , для которых . Отсюда следует, что

    (1)

При этом можно считать выполненными неравенства

Рекомендуемые материалы

 .(2)

Если такое неравенство для , например, не имеет места, можно разделить на . Для

Рекомендация для Вас - 1 Правоохранительная система государства и адвокатура.

 любого целого  из (1) вытекает

. При ограничениях типа (2)  находятся однозначно. Имеем

. Числа  - взаимно простые. Следовательно имеем для любого целого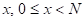

. Теперь . Раскрывая скобки и отбрасывая члены кратные , получим показатель вида .

Из равенства  следует, что , поэтому весь показатель сравним с . Это означает, что . Вводя обозначения , окончательно получим  =

. Это означает, что преобразование Фурье для  точек свелось к последовательному выполнению преобразования Фурье по  точкам, а затем - по  точкам результатов предыдущего преобразования. При этом потребуется не более, чем  умножений. По сравнению с  выигрыш небольшой. Если же для какого-либо из промежуточных случаев есть своя быстрая схема, выигрыш может получиться значительным.